Кафедра «Программное обеспечение вычислительной техники
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ДГТУ)
Кафедра «Программное обеспечение вычислительной техники
И автоматизированных систем»
УТВЕРЖДАЮ:
Заведующий кафедрой ПОВТиАС
_________________ Карапетянц А.Н.
" ____ " _________________20___ г
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к учебной практике на тему:
«Решение нелинейных уравнений»
Практикант Жданов Дмитрий Евгеньевич Группа ВПР 11
Специальность 09.03.04 – Программная инженерия
Руководитель работы /В.Н. Землянухин /
Ростов-на-Дону
2016 г.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ДГТУ)
Кафедра «Программное обеспечение вычислительной техники
И автоматизированных систем»
УТВЕРЖДАЮ:
Заведующий кафедрой ПОВТиАС
_______________Карапетянц А.Н.
" ____ " ________________ 20___ г
ЗАДАНИЕ
На учебную практику
Студент Жданов Дмитрий Евгеньевич Группа ВПР 21
Тема Решение нелинейных уравнений
Срок представления отчета к защите "_____" 2016 г.
Исходные данные для учебной практики задание руководителя
Руководитель практики /Кузин.А.П./
Задание принял к исполнению _______________ /Жданов Д.Е./
«____» ___________2016 г
Содержание
1. Теоретическая часть. 4
1.1. Введение в методы решения уравнений. 4
1.2. Методы уточнения корней. 8
1.2.1 . Метод половинного деления. 8
1.2.2 . Метод простых итераций. 9
1.2.3 . Метод Ньютона (метод касательных) 10
1.2.4 . Модифицированный метод Ньютона (метод секущих) 12
1.2.5 . Метод хорд. 12
2. Алгоритмическое конструирование. 14
2.1. Пояснение задачи. 14
2.2. Метод половинного деления. 17
2.3. Метод простых итераций. 18
2.4. Метод Ньютона (метод касательных) 18
2.5. Метод хорд. 19
3. Программное конструирование. 20
3.1. Программная среда PascalABC.NET. 20
3.2. Программная реализация………………………………………..22
4. Анализ результатов расчета. 25
5. Вывод. 26
6. Список использованных источников. 27
Теоретическая часть
Методы уточнения корней
Метод половинного деления
Дано нелинейное уравнение:
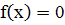
Найти корень уравнения, принадлежащий интервалу [a,b], с заданной точностью ɛ.
Для уточнения корня методом половинного деления последовательно осуществляем следующие операции:
- Делим интервал пополам:
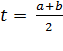 - координаты середины отрезка[a,b]
- координаты середины отрезка[a,b]
- В качестве нового интервала изоляции принимаем ту половину интервала, на концах которого функция имеет разные знаки (Рисунок 4).
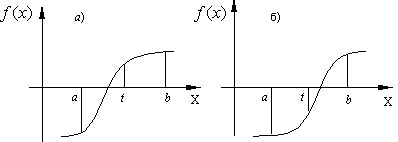
Рисунок 4 – Интервалы изоляции.
Для этого:
a) Вычисляем значение функции f(x) в точках a и t.
b) Проверяем: если f(a)f(t) < 0, то корень находится в левой половине интервала [a,b] (Рисунок 4.а). Тогда отбрасываем правую половину интервала и делаем переприсвоение b=t.
c) Если f(a)f(t) < 0 не выполняется, то корень находится в правой половине интервала [a,b] (рисунок 4.а). Тогда отбрасываем левую половину и делаем переприсвоение a=t. В обоих случаях мы получим новый интервал [a,b] в 2 раза меньший предыдущего.
d) Процесс, начиная с пункта 1, циклически повторяем до тех пор, пока длина интервала [a,b] не станет равной либо меньшей заданной точности, т.е.
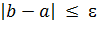
Метод простых итераций
В ряде случаев весьма удобным приемом уточнения корня уравнения является метод последовательных приближений (метод итераций).
Пусть с точностью 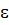 необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.
необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.
Для применения этого метода исходное уравнение f(x)=0 должно быть приведено к виду:
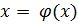 (2)
(2)
В качестве начального приближения x0 выбираем любую точку интервала [a,b].
Далее итерационный процесс поиска корня строится по схеме:
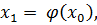
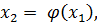 (4.3)
(4.3)
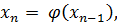
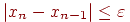 (4.4) (4.4) |
В результате итерационный процесс поиска реализуется рекуррентной формулой (4.3). Процесс поиска прекращается, как только выполняется условие (4.4) или число итераций превысит заданное число N.
Для того, чтобы последовательность х1, х2,…, хn приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:
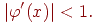 | (4.5) |
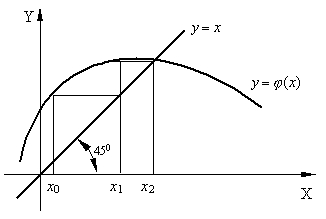
Рисунок 5 – Геометрический смысл метода
Метод хорд
Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня.
При этом в процессе поиска семейство хорд может строиться:
а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х0=b (Рисунок 7а);
б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х0=a (Рисунок 7б);
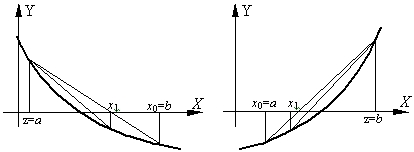
Рисунок 7а,б - Геометрический смысл метода
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:
для случая а)
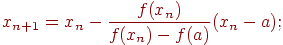 | (4.11) |
для случая б)
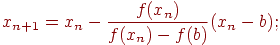 | (4.12) |
Процесс поиска продолжается до тех пор, пока не выполнится условие:
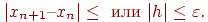 | (4.13) |
Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f"(z) совпадают.
Пояснение задачи
Реализовать программу для решения нелинейных уравнений.
Методами:
1. Половинного деления.
2. Простых итераций.
3. Ньютона (метод касательных).
4. Хорд.
С помощью программной среды Pascal ABC.NET.
В качестве проверки работоспособности программы решить уравнения:
x4-3x+1=0
lgx=10-x
Выявить самый быстрый и действенный метод решения.
Для выполнения задания функция x4-3x+1=0 была протабулирована с шагом 0,2 на отрезке [0.1;4].
| X | Y |
| 0.1 | 0.7001 |
| 0.3 | 0.1081 |
| 0.5 | -0.4375 |
| 0.7 | -0.8599 |
| 0.9 | -1.0439 |
| 1.1 | -0.8359 |
| 1.3 | -0.0439 |
| 1.5 | 1.5625 |
| 1.7 | 4.2521 |
| 1.9 | 8.3321 |
| 2.1 | 14.1481 |
| 2.3 | 22.0841 |
| 2.5 | 32.5625 |
| 2.7 | 46.0441 |
| 2.9 | 63.0281 |
| 3.1 | 84.0521 |
| 3.3 | 109.6921 |
| 3.5 | 140.5625 |
| 3.7 | 177.3161 |
| 3.9 | 220.6441 |
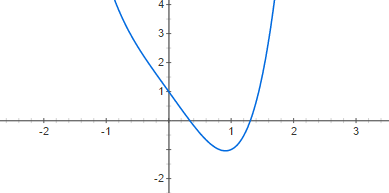
Рис. 8 - График функции x4-3x+1=0 .
Для выполнения задания функция lgx=10-x была протабулирована c шагом 0,2 на отрезке [0.1;4].
| X | Y |
| 0.1 | -1.7943 |
| 0.3 | -1.0241 |
| 0.5 | -0.6173 |
| 0.7 | -0.3544 |
| 0.9 | -0.1717 |
| 1.1 | -0.0380 |
| 1.3 | 0.0638 |
| 1.5 | 0.1445 |
| 1.7 | 0.2105 |
| 1.9 | 0.2662 |
| 2.1 | 0.3143 |
| 2.3 | 0.3567 |
| 2.5 | 0.3948 |
| 2.7 | 0.4294 |
| 2.9 | 0.4611 |
| 3.1 | 0.4906 |
| 3.3 | 0.5180 |
| 3.5 | 0.5438 |
| 3.7 | 0.5680 |
| 3.9 | 0.5909 |
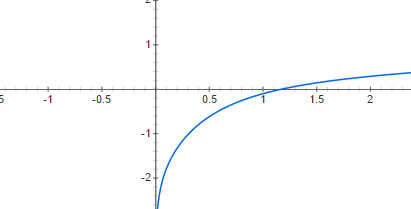
Рисунок 9 - График функции lgx=10-x.
Программное конструирование
Програмная реализация
const eps=0.001; //эпсилон погрешность
function function1(x:real):real; // функция x4-3x+1=0
begin
function1:=power(x,4)-3*x+1;//
end;
function diff1_func1(x:real):real; //первая производная первой функции
begin
diff1_func1:= 4*x*x*x;
end;
function diff2_func1(x:real):real; //вторая производная первой функции
begin
diff2_func1:=12*x;
end;
function function2(x:real):real; //функция lgx-10-x=0
begin
function2:=log10(x)-1/power(10,x);
end;
function diff1_func2(x:real):real; //первая производная второй функции
begin
diff1_func2:= (1/(x*ln(10)))+power(10,-x)*ln(10);
end;
function diff2_func2(x:real):real; //вторая производная второй функции
begin
diff2_func2:=x*(ln(10)-1/10)-ln(10)-power(10,-x)*(ln(10)*ln(10)-1/10);
end;
procedure dichotomy(var a,b:real); //метод дихотомии
var t,f1,f2,x:real;
iteration: integer;
begin
iteration:=0;
repeat
t:=(a+b)/2;
f1:=function1(a);
f2:=function1(t);
if (f1*f2<=0) then b:=t
else
begin
a:=t;
f1:=f2;
end;
iteration:=iteration+1;
until abs(b-a)<=eps;
x:=(a+b)/2;
writeln('Корень: x = ',x:10:6);
writeln('Функция: f(x) = ',function1(x));
writeln('Кол-во итераций: ',iteration);
end;
procedure chord(var a,b:real); //метод хорд
var f,f2,fz,z,x,h:real;
iteration: integer;
begin
iteration:=0;
f:=function1(a);
f2:=diff2_func1(a);
if (f*f2>0) then
begin
x:=b;
z:=a;
end
else
begin
x:=a;
z:=b;
end;
fz:=function1(z);
repeat
f:=function1(x);
h:=((x-z)*f)/(f-fz);
x:=x-h;
iteration:=iteration+1;
until (abs(h)<=eps);
writeln('Корень: x = ',x:10:6);
writeln('Функция: f(x) = ',function1(x):1:13);
writeln('Кол-во итераций: ',iteration);
end;
procedure newton(var a,b:real); //метод Ньютона
var f,f1,f2,x,h:real;
iteration: integer;
begin
iteration:=0;
f:=function2(b);
f2:=diff2_func2(b);
if (f*f2>0) then x:=b else x:=a;
repeat
f:=function2(x);
f1:=diff1_func2(x);
h:=f/f1;
x:=x-h;
iteration:=iteration+1;
until (abs(h)<=eps);
writeln('Корень: x = ',x:10:6);
writeln('Функция: f(x) = ',function2(x):1:13);
writeln('Кол-во итераций: ',iteration);
end;
function phix(var x,lamb:real):real; //дополнительная функция fi(x)
begin
phix:=x-lamb*(log10(x)-power(10,-x));
end;
procedure iterations(var a,b:real); //метод простых итераций
var iteration:integer;
x,x0,lamb:real;
begin
iteration:=0;
x:=(a+b)/2;
if (diff1_func2(a)>diff1_func2(b)) then lamb:=1/diff1_func2(a)
else lamb:=1/diff1_func2(b);
repeat
x0:=x;
x:=phix(x0,lamb);
iteration:=iteration+1;
until (abs(x-x0)<=eps);
writeln('Корень: x = ',x:10:6);
writeln('Функция: f(x) = ',function2(x):1:13);
writeln('Кол-во итераций: ',iteration);
end;
BEGIN
var a,b:real;
a:=0.1; //функция имеет два корня, поэтому вычисляем на двух промежутках
b:=1; //границы первого промежутка
writeln('Первая функция: x^4-3*x+1');
writeln;
writeln('Метод дихотомии');
dichotomy(a,b);
writeln;
a:=1; //границы второго промежутка
b:=1.5;
dichotomy(a,b);
writeln;
a:=0.1; //границы первого промежутка
b:=1;
writeln('Метод хорд');
chord(a,b);
writeln;
a:=1; //границы второго промежутка
b:=1.5;
chord(a,b);
writeln();
writeln('Вторая функция: lg(x)-10^-x');
writeln;
writeln('Метод Ньютона');
newton(a,b);
writeln;
writeln('Метод простых итераций');
a:=0.1;
b:=1.5;
iterations(a,b);
END.
Анализ результатов расчета.
Границы интервала: а = 0.1, b = 1.5.
Метод дихотомии:
x1 = 0.337744, количество итераций = 10
x2 = 1.307129, количество итераций = 9
Метод хорд:
x1 = 0.337674, количество итераций = 4
x2 = 1.307306, количество итераций = 6
Метод Ньютона:
x = 1.168905, количество итераций = 4
Метод итераций:
x = 1.167165, количество итераций = 11
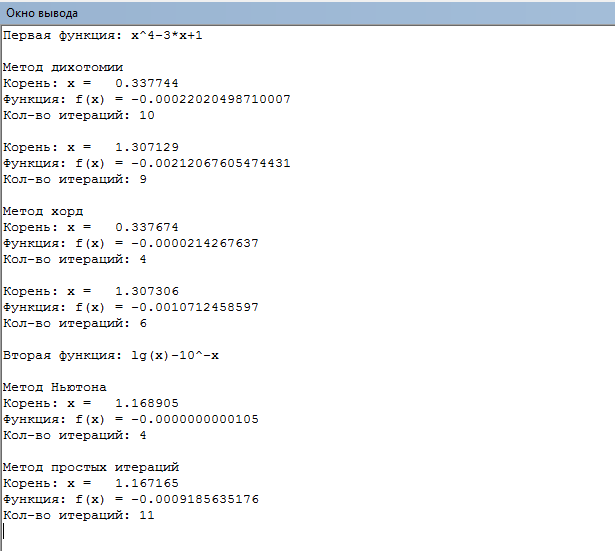
Рисунок 14 - Демонстрация работы программы
Вывод
Были рассмотрены методы уточнения действительных корней при решении нелинейных уравнений, а именно:
1. Метод половинного деления;
2. Метод простых итераций;
3. Метод Ньютона (метод касательных);
4. Метод хорд.
Была разработана программа, реализующая вышеперечисленные методы с точностью 0.0001, с помощью среды программирования Pascal ABC.NET.
Разработанная программа находит действительные корни для уравнений:
x4-3x+1=0
lgx=10-x
Для уравнения x4-3x+1=0 действительные корни находятся при помощи методов дихотомии и хорд.
Результаты выполнения программы показали, что метод хорд выполняется за минимальное число итераций.
Для уравнения lgx=10-x действительные корни находяться при помощи методов простых итераций и Ньютона.
Результаты выполнения программы показали, что метод Ньютона выполняется за минимальное число итераций.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ДГТУ)
Кафедра «Программное обеспечение вычислительной техники
