Алгоритм метода наискорейшего спуска

При заданной точке x алгоритм наискорейшего спуска заключается в реализации линейного поиска вдоль направления -grad(f(x))/||grad(f(x))|| или, что то же самое, вдоль направления -grad(f(x)).

Начальный этап. Пусть eps > 0 - константа остановки. Выбрать начальную точку x1, положить k=1 и перейти к основному этапу.

Основной этап. Если ||grad(f(x))|| < eps , то остановиться; в противном случае положить dk = -grad(f(x)) и найти lym[k] - оптимальное решение задачи минимизации f(xk + lym*dk) при lym >= 0. Положить x[k+1]=xk+lym[k]*dk, заменить k на k+1 и повторить основной этап.

Численное интегрирование

Постановка задачи

Вычисление скалярных аддитивных величин обычно сводится к суммированию бесконечно большого числа беcконечно малых слагаемых такого вида:

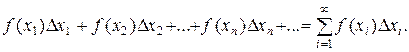
Например, если значение функции f(x_i) считать проекцией силы на ось Ох, а малую величину Dх_i - “элементарным” перемещением некоторой массы под действием этой силы, то произведение f(x_i) Dх_i = DА_i даст “элементарную” работу DА_i силы f на малом перемещении Dх_i. Работа силы f на всем перемещении массы по свойству аддитивности будет равна сумме “элементарных” работ

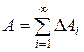
Но так как физически не представляется возможным просуммировать бесконечно много слагаемых DА_i, то, ограничиваясь n слагаемыми, можно получить приближенное значение данной величины:

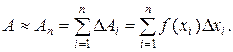
Точное значение таких величин выражается с помощью предельного перехода, в результате которого получают интеграл:

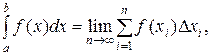
где [a; b] - отрезок, на котором задана функция f.

Определение понятия интеграла и его геометрическую интерпретацию.

Пусть на конечном отрезке [a; b] задано непрерывную функцию f (рисунок 3), причем f(x) > 0, x Î [a; b] и a < b.

1.Разобьем отрезок [a; b] произвольным образом на n частичных отрезков точками:

a = x₀ < x₁ < x₂ <...< x_i < x_i+1 < ... < x_n = b.

2.Обозначим длину каждого частичного отрезка через

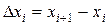(i = 0, 1, 2,...,n - 1).

3.Выберем произвольно в каждом частичном отрезке точку

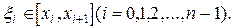
4.Составим произведения значений функции f в точке 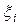на длину i-го отрезка, т.е.

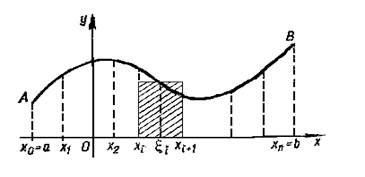
Рисунок 4

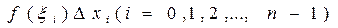
Геометрически это произведение дает площадь “элементарного” i-го прямоугольника, заштрихованного на рисунке 4.

Просуммируем полученные произведения

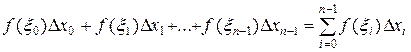: (1)

Полученную таким образом сумму (1) называют интегральной суммой. Геометрически эта сумма дает площадь всех n ’’элементарных’’ прямоугольников, то есть площадь ступенчатой фигуры. Отметим, что интегральных сумм (1) можно построить бесконечно много в силу того, что при их построении допускается два произвола: разбиение отрезка [a, b] на части точками х_i и выбор точек 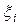(i = 0, 1, ... ,n-1) на каждом из частичных отрезков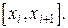

6. Выполним предельный переход при условии, что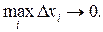

Если при 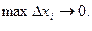интегральная сумма (1) имеет конечный предел, то этот предел называется интегралом функции f от а до b и обозначается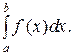

Следовательно, 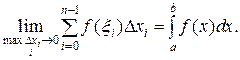(2)

Таким образом, интегралом функции f на отрезке интегрировании от а до b называется предел интегральных сумм при условии, что максимальная длина частичных отрезков стремится к нулю, следовательно, число их неограниченно возрастает, то есть .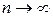

В силу непрерывности функции f площадь ступенчатой фигуры (рис.33) при большом n “почти совпадает” с площадью криволинейной трапеции аAвb, а при 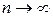интеграл (2) и дает точное значение площади S криволинейной трапеции с основанием [a; b], ограниченной сверху графиком функции f:

S =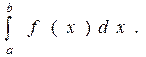

Можно доказать, что если функции f непрерывна на отрезке [a; b], то предел (2) существует.

Формула (2) непригодна для точного вычисления интеграла, так как операция вычисления предела интегральной суммы практически не всегда легко выполнима.

Для вычисления точного значения интеграла (2) используют понятие первообразной функции. Пусть подынтегральная функция f непрерывна на отрезке [a; b] и известна ее первообразная F, то есть такая функция, что

F‘(x) = f(x), x 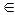[a; b].

Тогда интеграл (2) может быть вычислен по формуле Ньютона-Лейбница

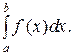= F(b) - F(a), (3)

как приращение первообразной функции F на отрезке [a; b].

Кроме того, можно доказать, что если существует интеграл (3), то одной из первообразных функций на [a;b] для подынтегральной функции является интеграл с переменным верхним пределом 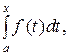так как

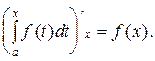
Таким образом, если мы умеем найти первообразную функцию, то можем вычислить также и интеграл.

Однако очень часто нахождение первообразной функции затруднительно, громоздко или вообще невыполнимо в элементарных функциях. Тогда задача вычисления точного значения интеграла по формуле Ньютона-Лейбница (3) оказывается неразрешимой. Класс функций f, для которых первообразная F выражается через элементарные функции, весьма узок, а , значит, и формула (3) не всегда пригодна для практики. Например, не выражается в элементарных функциях первообразная для функции

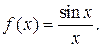
В таких случаях действие интегрирования порождает новый класс неэлементарных функций. Так, для приведенной выше функции получаем (по определению) неэлементарную функцию

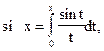(4)

которую называют интегральным синусом. Значение этой функции, например, при х = 1 равно 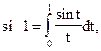то есть значением функции является интеграл, не выражающийся в элементарных функциях, а не число в явном виде, что было бы практически значительно удобнее. Кроме того, на практике часто подынтегральная функция f задается графически или таблично, тогда само понятие первообразной теряет смысл и формула Ньютона - Лейбница, несмотря на ее большое теоретическое и практическое значение, опять “не работает”.

Таким образом, приходится иметь дело с интегралами, которые не выражаются в элементарных функциях. В этих случаях незаменимое значение приобретает приближенное интегрирование. Для приближенного интегрирования функций разработано много численных методов. Сущность этих методов состоит в том, что значение интеграла вычисляется приближенно по формулам вида

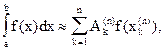(5)

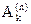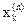в которых используется ряд значений подынтегральной функции. Формулу (и сумму) вида (5) называют квадратурной. Действительные числа и называют соответственно коэффициентами и узлами квадратурной формулы (5). Величину

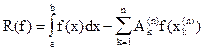(6)

называют остаточным членом (или погрешностью) квадратурной формулы (5).

Заменяя интеграл квадратурной суммой, мы пренебрегаем остаточным членом R(f) (это погрешность метода). Выполняя вычисления по формуле (5), всегда оперируют не с точными, а с приближенными значениями подынтегральной функции 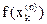и коэффициентов 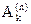. Погрешность, с которой заданы значения 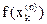и 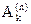, переносится и на квадратурную сумму (это так называемая неустранимая погрешность R₁ формулы (5)). Если 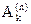- точные числа (с такими формулами мы будем иметь дело), а значения 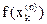вычислены с погрешностью D_f, то значение квадратурной суммы будет вычислено с неустранимой погрешностью

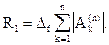
При нахождении квадратурной суммы все промежуточные вычисления рекомендуется проводить с 1 - 2 запасными цифрами. Это дает возможность пренебрегать погрешностями округлений в промежуточных вычислениях. Однако при отбрасывании запасных цифр в конечном результате необходимо учитывать заключительную погрешность округления D₀. Таким образом, суммарная погрешность численного интегрирования функций D представляет собой сумму трех указанных выше погрешностей:

D = R(f) + R₁ + D₀.

Геометрически общий подход к решению задачи приближенного интегрирования функций состоит в том, что в криволинейную трапецию, площадь которой равна искомому значению интеграла, вписывают (или описывают) «частичные» прямоугольники, трапеции или параболы, находят их площади, а затем суммируют. В результате получают приближенное значение искомого интеграла, так как при этом график функции f заменяют некоторой ломаной линией. В соответствии с выбором геометрической фигуры для вычисления интеграла различают формулы: прямоугольников, трапеций, парабол (Симпсона). Для получения этих формул отрезок интегрирования [a; b] делят на частичные отрезки равной длины.

2. Формула прямоугольников

Для вычисления приближенного значения интеграла 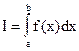отрезок [a; b] делят на n равных частей точками а = х₀ < x₁ < x₂ < ... < x_n = b так, что 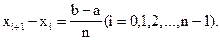Тогда длина каждого частичного отрезка 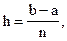а точки разбиения х₀ = а; x₁ = a + h; x₂ = a + 2h; ... ; x_n-1 = a + (n-1)h; x _n = a + nh = b образуют арифметическую прогрессию с разностью h. Эти точки называют узлами, а h - шагом интегрирования. Затем в узлах вычисляют ординаты y₀, y₁, y₂, ..., y_n то есть y_i = f(x_i) для х_i = a + ih (i=0, 1, 2,...,n). На частичных отрезках [x_i, x_i+1] строят прямоугольники (рисунок 5 – 6), высота которых равна значению f(x) в какой-либо точке каждого частичного отрезка.

Тогда произведение f(x_i) * h дает площадь частичного прямоугольника, а сумма таких произведений дает площадь ступенчатой фигуры, представляющую собой приближенное значение интеграла.

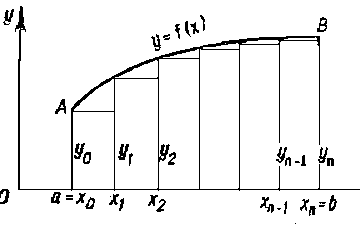
Рисунок 5

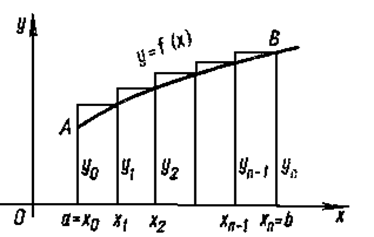
Рисунок 6

Если f(x_i) вычисляют (рис.5) в левых концах отрезков [x_i, x_i+1], то получают формулу левых прямоугольников вида:

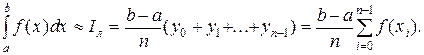
Если f(x_i) вычисляют (рис.6) в правых концах отрезков [x_i, x_i+1], то получают формулу правых прямоугольников вида:

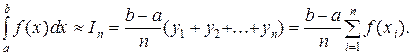
Если же функцию f вычисляют в точках x_i + 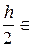[x_i, x_i+1], то получают формулу средних прямоугольников вида:

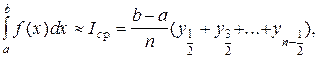(7)

где

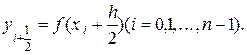
В том частном случае, когда функция f монотонно возрастает на [a; b] (рис.8.2.1), величина I_л дает значение интеграла I с недостатком (ломанная вписана в криволинейную трапецию), а величина I_п - с избытком (ломаная описана). Их среднее арифметическое значение дает более точный результат:

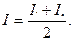
3. Формула трапеций

Формулу трапеций получают аналогично формуле прямоугольников, но на каждом частичном отрезке строится трапеция (рис.7).

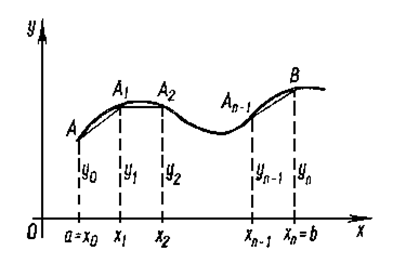
Рисунок 7

Тогда площадь криволинейной трапеции аАВb приближенно равна площади фигуры, ограниченной ломаной линией аАА₁А₂...А_n-1Bb. Площади частичных трапеций:

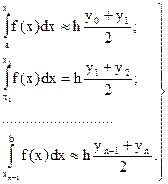(8)

Суммируя равенства (8), получим формулу трапеций:

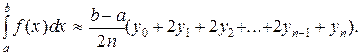(9)

4. Формула Симпсона

Для построения формулы Симпсона предварительно рассмотрим такую задачу: вычислить площадь S криволинейной трапеции, ограниченной сверху графиком параболы y = Ax² + Bx + C, слева прямой х = - h, справа прямой x = h и снизу отрезком [-h; h]. Пусть парабола проходит через три точки (рис.8): D(-h; y₀) E(0; y₁) и F(h; y₂), причем х₂ - х₁ = х₁ - х₀ = h. Следовательно,

x₁ = x₀ + h = 0; x₂ = x₀ + 2h.

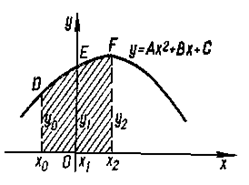
Рисунок 8

Тогда площадь S равна интегралу:

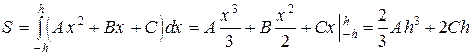. (11)

Выразим эту площадь через h, y₀, y₁ и y₂. Для этого вычислим коэффициенты параболы А, В, С. Из условия, что парабола проходит через точки D, E и F, имеем:

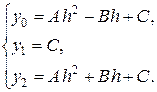
Решая эту систему, получаем:

C = y₁;

A =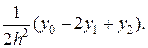

Подставляя эти значения А и С в (11), получаем искомую площадь

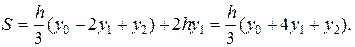(12)

Перейдем теперь к выводу формулы Симпсона для вычисления интеграла

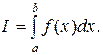
Для этого отрезок интегрирования [a; b] разобьем на 2n равных частей длиной 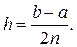В точках деления (рис.40)

а = х₀, х₁, х₂, ...,х_2n-2, x_2n-1, x_2n = b

вычисляем значения подынтегральной функции f:

y₀, y₁, y₂, ...,y_2n-2, y_2n-1, y_2n,

где y_i = f(x_i), x_i = a + ih (i = 0, 1, 2,...,2n).

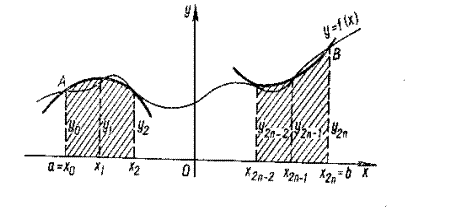
Рисунок 9

На отрезке [x₀; x₂] подынтегральную функцию заменяем параболой, проходящей через точки (x₀; y₀), (x₁; y₁) и (x₂; y₂), и для вычисления приближенного значения интеграла от х₀ до х₂ воспользуемся формулой (12). Тогда (на рис. 9 заштрихованная площадь):

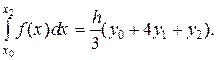
Аналогично находим:

................................................

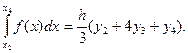
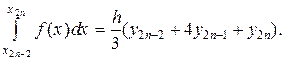
Сложив полученные равенства, имеем:

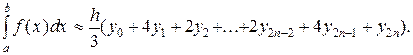
Или

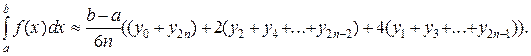(13)

Формула (13) называется обобщенной формулой Симпсона или формулой парабол, так как при ее выводе график подынтегральной функции на частичном отрезке длины 2h заменяется дугой параболы.

5. Оценка точности формул интегрирования

При приближенном интегрировании функций необходимо знать погрешность, с которой получено приближенное значение интеграла, так как без нее полученный результат не представляет ценности. Из геометрического смысла интеграла ясно, что каждая из рассмотренных формул дает результат тем точнее, чем больше n, и что наиболее точной является формула Симпсона, а наименее точными – формулы правых и левых прямоугольников. Однако увеличение nведет к возрастанию объема вычислительной работы, что нежелательно, особенно при ручных вычислениях на ЭКВМ.

В математическом анализе выводят формулы для оценки погрешности R приближенного интегрирования, имеющие вид для

1) формулы средних прямоугольников

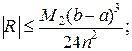(15)

2) формулы трапеций:

(16)

3) формулы Симпсона:

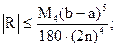(17)

где 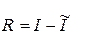; 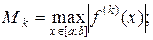(b-a) – длина отрезка интегрирования; I – точное значение интеграла; 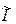– приближенное значение интеграла, вычисленное по формуле средних прямоугольников, трапеций или Симпсона.

Пользуясь этими формулами, можно по заранее заданной точности 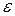приближенно вычислить необходимое число отрезков n. Ясно, что формулы (15), (16) и (17) неприменимы, если функция f задана графически или таблично. Практически ими редко пользуются и при аналитическом задании функции f, так как вычисление производных f^(k)(х) и их оценка обычно весьма трудоемки. Кроме того, промежуточные результаты (ординаты, их суммирование и т. п.) вычисляются приближенно и с округлением, поэтому в окончательном результате надо учитывать и эти погрешности.

При вычислениях на ЭВМ для оценки погрешности интегрирования используется так называемый метод автоматического выбора шага интегрирования для достижения заданной точности. Алгоритм этого метода состоит из следующих этапов:

1. Выбирается начальное значение nи вычисляется шаг интегрирования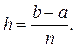

2. Вычисляется значение интеграла I_hдля этого начального шага h.

3. Затем шаг hуменьшается в два раза ( 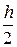), и для него вычисляется значение интеграла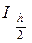

4. Сравниваются полученные два значения

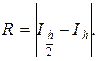
5. Полученная погрешность Rсравнивается с заранее заданной точностью 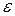. Если R > 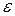, то точность не достигнута, и величине I_h присваивается более точное значение 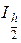, после чего повторяются этапы 3, 4 и 5 до выполнения условия R .

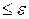6. При выполнении условия R 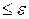за искомое значение интеграла Iпринимается последнее значение величины .

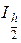Этот алгоритм реализуется в стандартной подпрограмме вычисления значения интеграла по формуле Симпсона с заранее заданной точностью 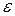. Она включается в библиотеку стандартных подпрограмм (БСП) современных вычислительных машин. Причем число делений заданного отрезка интегрирования выбирается из ряда чисел, начиная с n = 16, то есть n = 16, 32, 64, 128, ..., представляющих собой степени основания двоичной системы счисления (2⁴; 2⁵; ...). Такой выбор обусловлен точностью преобразования этих чисел из десятичной системы счисления в двоичную.

При вычислениях на ЭВМ по формуле Симпсона для достижения заданной точности в три – четыре значащие цифры, как правило, табулируют функцию при n = 16 (17 ординат) и вычисляют интеграл I₁₆, затем вычисляют интеграл с удвоенным шагом I₈, делая выборку значений функции через одно и оставляя в промежуточных вычислениях до шести значащих цифр.

В качестве приближенного значения интеграла принимают значение I_2N, руководствуясь при этом таким практическим правилом: считается, что в I_2N, точных значащих цифр на одну больше, чем совпадающих цифр в I_N, и I_2N. Погрешность I_2Nне превосходит числа

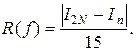
Если приближенное значение интеграла вычисляют по формулам средних прямоугольников или трапеций с двойным пересчетом (то есть с вычислением I_N, и I_2N), то для оценки погрешности I_2Nприближенного интегрирования получают

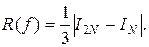
Поскольку вычисление и оценка производных f^(k)(x) (k=2,4) обычно трудоемки, то в формулах (15) - (17) вместо производных часто используют отношения соответствующих конечных разностей к шагу интегрирования, то есть полагают

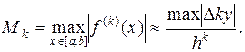
Аналогично оценивают погрешность квадратурных формул и в тех случаях, когда подынтегральная функция задана таблично или графически.

Численное дифференцирование

В инженерной практике довольно часто приходится встречаться с обыкновен­ными дифференциальными уравнениями при решении различных прикладных задач. Обыкно­венным дифференциальным уравнением называется выражение вида

F(X,Y,Y',Y”,...,Y ^n-1 ,Y ⁿ ) = 0 , (1)

где Х - независимая переменная;

Y - искомая функция от Х;

Y',Y»,...,Yⁿ -производные порядка 1,2,...,n.

Порядок старшей производной, входящей в уравнение (1), называется порядком дифференциального уравнения.

Простейшим обыкновенным дифференциальным уравнением является уравнение 1-го порядка

y'= f(x,y) (2).

Основная задача, относящаяся к этому уравнению, есть задача Коши: найти реше­ние дифференциального уравнения (2) в виде у=у(х), удовлетворяющее начальному усло­вию Y(Xo)=Yo, т.е. требуется найти интегральную кривую у=у(х), проходящую через заданную точку М(Хо,Yo).

Для нахождения решения дифференциального уравнения (1) необ­ходимо задать та­кое количество начальных условий, какое соответствует порядку старшей производ­ной, а именно задать значения

Yo=Y(Xo); Yo'=Y'(Xo),...,Y₀ ^n-1 = Y^n-1 (Xo) (3)

Уравнение (1) называется разрешенным относительно старшей производной, если оно имеет вид

Y⁽ⁿ⁾ =f(X,Y,Y',Y»,...,Y^n-1 ) (4)

Если дифференциальное уравнение (1) разрешимо относительно старшей произ­водной, то его можно свести к системе обыкновенных дифференциаль­ных уравнений 1-го порядка заменой на неизвестную функцию Р₁(х), у» на Р₂(х) и т.д.

Таким образом, имеем

y'=P₁,

P1'=P₂,

P2'=P₃,

...

P'n-1 = f (x,y,P₁,P₂,...,P_n-1), причем

Y(Xo)=Yo

P₁(Xo)=Yo'

P₂(Xo)=Yo»

. . . . . . . . .

P _n-1(Xo)=Yo^n-1 .

При решении инженерных задач чаще всего приходится иметь дело с уравне­ниями, общее решение которых не выражается в аналитическом виде. Поэтому возникает необходимость применять те или иные методы, дающие приближенное ре­шение задачи.

6.1 Метод Эйлера

Метод численного решения дифференциального уравнения 1-го по­рядка

y'=f(x,y) (7)

с начальным условием Y(Xo)=Yo основан на разложении решения в ряд Тейлора в h-окрестности точки Хо:

Y1 = Y(x+h) = Y(Xo) + h*Y'(Xo) + (h²/2)*Y»(Xo) +...

При отбрасывании всех членов ряда, содержащих производные 2-го и высших порядков, получим

Y1 = Yo + h*f(Xo,Yo),

где f(x,y) - правая часть уравнения (7). Пользуясь значением Y1 из разложения y(x) в h –окрестности точки Х1=Хо+h, получим

Y2=Y1+h*f(X1,Y1),

аналогично продолжая для следующей Х i+1 точки, получим

Y i+1 = Yi+h*f(Xi,Yi). (8)

Если дано уравнение 2-го порядка

Y»=f(x,y,y') (9)

c начальными условиями Y(Xo)=Yo и Y'(Xo)=Yo', то такое уравнение можно свести к системе двух уравнений 1-го порядка

у'=P (10)

P'=f(x,y,y'),

причем

Y(Xo)=Yo, (11)

P(Xo)=Po=Yo'.

Тогда приближенные значения функций у и Р в точке можно вы­числить

Y_i+1 = Y_i+h*P_i (12)

P_i+1 = P_i+h*f(X_i, Y_i, P_i),

где f( Xi, Yi, Pi) - правая часть уравнения (9).

При достаточно малой величине шага h метод Эйлера дает реше­ние с большой

точностью, т.к. погрешность решения близка к h².

Разновидностью рассмотренного выше метода Эйлера, известного в литературе также как метод Эйлера-Коши, является метод Эйлера-Коши с итерациями. Он заключается в вычислении на каждом шаге начального значения

Y⁰_i+1=Y_i+hF(x_i ,Y_i).

Затем с помощью итерационной формулы

Y^к_i+1=Y_i + 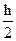+ [ F(x_i, Y_i) + F(x_i+1, ]

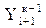решение уточняется. Итерации проводят до тех пор, пока совпадает заданное число цифр результата на двух последних шагах итераций. Погрешность метода составляет примерно h³. Обычно число итераций не должно превышать 3-4, иначе нужно уменьшить шаг h.

Модифицированный метод Эйлера второго порядкареализуется следующими рекуррентными формулами:

Y_i+1 = Y_i + hF(x_i + h/2, Y^*_i+1/2 ),

где Y^*_i+1/2 = Y_i + hF(x_i , Y_i)/2 . Метод дает погрешность порядка h³ и имеет меньшее время вычислений, поскольку вместо нескольких итераций производится вычисление только одного значения Y^*_i+1/2.

Метод трапеций – одна из модификаций метода Эйлера второго порядка. Он реализуется применением на каждом шаге формулы

Y_i+1 = Y_i + 0.5(K₁+K₂)

где K₁ = h F(x_i,Y_i);

K₂ = h F(x_i+h,Y_i+K₁)

и дает погрешность порядка h³. Этот метод относится к общим методам Рунге-Кутта.

Метод Рунге-Кутта

Метод Рунге-Кутта является наиболее распространенным ме­тодом решения дифференциальных уравнений при постоянном заданном шаге. Его достоинством является высокая точ­ность.

Алгоритм реализации метода Рунге-Кутта для уравнений 1-го порядка (типа (7)) заключается в циклических вычислениях Y i+1 на каждом i+1 шаге по следующим формулам:

K1=h*F(Xi,Yi);

K2=h*F(Xi+h/2,Yi+K1/2);

K3=h*F(Xi+h/2,Yi+K2/2);

K4=h*F(X+h,Y+K3);

Y i+1 = Yi + (K1+2*K2+2*K3+K4) / 6 . (13)

Для дифференциальных уравнений 2-го порядка (типа (9)) метод реализуется с помощью следующих формул:

K1=h*F(Xi; Yi; Yi');

K2=h*F(Xi+h/2; Yi+h/2*(Yi'+K1/4); Yi'+K1/2);

K3=h*F(Xi+h/2; Yi+h/2*(Yi'+K1/4); Yi'+K2/2);

K4=h*F(Xi+h; Yi+h*Yi'+h/2*K3; Yi'+K3);

Y i+1 = Yi+h*[Yi'+(K1+K2+K3)/6];

Y'i+1 = Yi'+(K1+2*K2+2*K3+K4)/6. (14)

Перед началом вычислений надо задать шаг h и начальные усло­вия (3).