Методы безусловной минимизации функций многих переменных.

Многомерный поиск без использования производных.

Рассмотрим методы решения минимизации функции нескольких переменных f, которые опираются только на вычисление значений функции f(x), не используют вычисление производных, т.е. прямые методы минимизации. В основном все описанные методы заключаются в следующем. При заданном векторе х определяется допустимое направление d. Затем, отправляясь из точки х, функция f минимизируется вдоль направления d одним из методов одномерной минимизации. Задача линейного поиска заключается в минимизации f(x+lym*d) при условии, что lym принадлежит L, где L обычно задается в форме L=E1, L={lym: lym >= 0} или L={l: a<=lym<=b}. Будем предполагать, что точка минимума lym* существует. Однако в реальных задачах это предположение может не выполняться. Оптимальное значение целевой функции в задаче линейного поиска может быть не ограниченным или оптимальное значение функции конечно, но не достигается ни при каком lym.

Метод циклического покоординатного спуска.

В этом методе в качестве направлений поиска используются координатные векторы. Метод циклического покоординатного спуска осуществляет поиск вдоль направлений d1, ..., dn, где dj - вектор, все компоненты которого, за исключением j-ого, равны нулю. Таким образом, при поиске по направлению dj меняется только переменная xj, в то время как все остальные переменные остаются зафиксированными.

Алгоритм циклического покоординатного спуска

Начальный этап.Выбрать eps >0, которое будет использоваться для остановки алгоритма, и взять в качестве d1, ..., dn координатные направления. Выбрать начальную точку x1, положить y1 = x1, k=j=1 и перейти к основному этапу.

Основной этап.

Шаг 1. Положить lymj равным оптимальному решению задачи минимизации f(yj+lym*dj) при условии, что lym принадлежит E1. Положить y[j+1]= yj+lymj*dj. Если j < n, то заменить j на j+1 и вернуться к шагу 1. Если j=n, то перейти к шагу 2.

Шаг 2. Положить x[k+1] = y[n+1]. Если || x[k+1] - xk || < eps, то остановиться. В противном случае положить y1= x[k+1], j=1, заменить k на k+1 и перейти к шагу 1.

Метод Хука и Дживса.

Метод Хука и Дживса осуществляет два типа поиска - исследующий поиск и поиск по образцу. Первые две итерации процедуры показаны на рисунке.

При заданном начальном векторе x1 исследующий поиск по координатным направлениям приводит в точку x2 . Последующий поиск по образцу в направлении x1- x2 приводит в точку y. Затем исследующий поиск, начинающийся из точки y, дает точку x3. Следующий этап поиска по образцу вдоль направления x3- x2 дает y*. Затем процесс повторяется.

Алгоритм Хука и Дживса с использованием одномерной минимизации.

Рассмотрим вариант метода, использующий одномерную минимизацию вдоль координатных направлений d1,..., dn и направлений поиска по образцу.

Начальный этап. Выбрать число eps > 0 для остановки алгоритма. Выбрать начальную точку x1, положить y1= x1, k=j=1 и перейти к основному этапу.

Основной этап.

Шаг 1. Вычилить lymj - оптимальное решение задачи минимизации f(yj+lym * dj) при условии lym принадлежит E1. Положить y[j+1]= yj+lymj*dj. Если j < n, то заменить j на j+1 и вернуться к шагу 1. Если j=n, то положить x[k+1] = y[n+1]. Если ||x[k+1] - xk|| < eps , то остановиться; в противном случае перейти к шагу 2.

Шаг 2. Положить d = x[k+1] - xk и найти lym - оптимальное решение задачи минимизации f(x[k+1]+lym*d) при условии lym принадлежит E1. Положить y1= x[k+1]+lym*d, j=1, заменить k на k+1 и перейти к шагу 1.

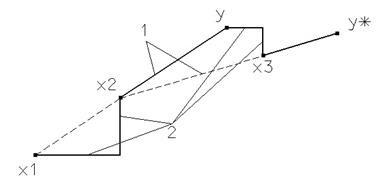1-поиск по образцу; 2- исследующий поиск вдоль координатных осей.

Многомерный поиск, использующий производные.

Пусть функция f(x) деференцируема в Еn . В этом разделе рассматривается итерационная процедура минимизации вида:

xk = x[k-1] + lym[k]*dk, k=1,... ,

где направление убывания dk определяется тем или иным способом с учетом информации о частных производных функции f(x), а величина шага lym[k] >0 такова, что

f(xk) < f(xk-1), k=1,2,....

Так как функция предполагается дифференцируемой, то в качестве критерия останова в случае бесконечной итерационной последовательности { xk }, как правило, выбирают условие ||grad(f(xk))||<eps, хотя, разумеется, могут быть использованы и другие критерии.

Метод наискорейшего спуска

Метод наискорейшего спуска является одной из наиболее фундаментальных процедур минимизации дифференцируемой функции нескольких переменных. Вектор d называется направлением спуска для функции f в точке x, если существует такое d > 0, что f(x+lym*d)<f(x) для всех lym принадлежащих интервалу (0, d). В частности, если

	f(x+ld)-f(x)
lim	-------------------< 0,	при lym->0+
	lym

то d - направление спуска. В методе наискорейшего спуска осуществляется движение вдоль направления d, для которого ||d|| = 1 и которое минимизирует приведенный выше предел. Если f дифференцируема в точке x и grad(f(x))!=0, то -grad(f(x))/||grad(f(x))|| является направлением наискорейшего спуска. В связи с этим метод наискорейшего спуска иногда называют градиентным методом.