Основные источники погрешностей.

Численные методы в настоящее время относятся к основным методам решения задач математики и различных ее приложений. Они характеризуются тем, что сводят процесс решения математической задачи к некоторой конечной последовательности операций над числами и приводят к результатам, представленным в виде чисел, числовых векторов и матриц, числовых таблиц и т. п.

В то же время полученные численными методами результаты обычно содержат погрешности, являясь лишь приближениями к искомым ответам. Оценка степени достоверности получаемых результатов является важнейшим вопросом при организации вычислительных работ. Это особенно важно при отсутствии опытных или других данных для сравнения, которые могли бы в некоторой степени показать надежность используемого численного метода и достоверность получаемых результатов.

Рассмотрим источники погрешностей на отдельных этапах решения задачи.

Математическая модель, принятая для описания данного процесса или явления, может внести существенные погрешности, если в ней не учтены какие-либо важные черты рассматриваемой задачи. Математическая модель задачи — это приближенное, идеализированное описание задачи на языке математики. При моделировании объекты и процессы задачи-оригинала, взаимосвязи между ее параметрами заменяются на математические понятия и соотношения.

Ради того чтобы получаемая в итоге математическая задача оказалась доступной для дальнейших исследований, учитывают лишь наиболее важные параметры, условия и особенности исходной задачи. Понятно, что чем меньше факторов отбрасывается, тем точнее получается модель. Кроме того, математическая модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других; поэтому важно правильно учитывать область ее применимости.

Несмотря на приближенность результатов математического моделирования, без него в приложениях математики не обойтись. Оно представляет собой обязательную ступень при переходе от нематематической задачи к математической. Более того, удовлетворительное исследование многих явлений реального мира оказывается возможным лишь тогда, когда удается построить их математические модели.

Исходные данные задачи часто являются основным источником погрешностей. Это так называемые неустранимые погрешности, поскольку они не могут быть уменьшены вычислителем ни до начала решения задачи, ни в процессе ее решения. Установить точные значения исходных параметров во многих случаях невозможно. Также, практика показывает, что следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других, как правило, не приводит к повышению точности результатов.

После того как математическая модель построена и определены исходные данные, необходимо подобрать метод решения полученной математической задачи. Круг математических методов условно подразделяется на аналитические, численные и графические методы.

Численный метод также является источником погрешностей. Это связано, например, с заменой интеграла суммой, усечением рядов при вычислениях значений функций, интерполированием табличных данных и т. п. Как правило, погрешность численного метода регулируема, т. е. она может быть уменьшена до любого разумного значения путем изменения некоторого параметра (например, шага интегрирования, числа членов усеченного ряда и т. п.). Погрешность метода обычно стараются довести до величины, в несколько раз меньшей погрешности исходных данных. Дальнейшее снижение погрешности не приведет к повышению точности результатов, а лишь увеличит стоимость расчетов из-за необоснованного увеличения объема вычислений.

Численные методы поиска решения делятся на точные и приближенные, а последние, в свою очередь на конечные и итерационные.

Для большинства реальных задач точных методов решения вообще не существует, а если они и имеются, то бывают настолько трудоемкими, что не представляют практического интереса. Кроме того, они часто сопряжены с бесконечными вычислительными процессами.

Например, поиск точного значения функции может свестись к нахождению суммы числового ряда, что в общем случае практически осуществить невозможно. Вследствие этого основным инструментом вычислительной математики являются приближенные численные методы, приводящие обычно к приближенным результатам даже приточных исходных данных и точных вычислениях. Возникают так называемые погрешности метода.

Конечные методы дают решение за фиксированное число математических операций, которое не изменяется в зависимости от исходных данных (алгоритм решения представляет собой простое вычисление неких формул). Время счета итерационными методами может быть рассчитано только приблизительно, т.к. поиск решения производится перебором возможных решений, и окончательный результат определяется по соответствию некоторого критерия желаемому значению. Время счета итерационными методами может в значительной степени варьироваться в зависимости от исходных данных.

На первый взгляд может показаться, что конечные методы предпочтительнее, но это не всегда верно. Вообще говоря, в терминах точной математики конечные методы дают точное решение. Тем не менее, результат вычислений конечными методами для некоторых задач может иметь очень большую ошибку. В итерационных методах (конечно, в зависимости от выбора критерия) такая ситуация практически невозможна: если процесс итераций сходится (т.е. критерий с каждым шагом приближается к желаемому значению), то будет получено решение, точность которого удовлетворяет выбранному критерию, если процесс расходится – решение (по крайней мере данным методом) найти невозможно.

Поскольку первые два типа погрешностей не находится в пределах компетенции вычислителя, то для вычислителя он служит лишь ориентиром точности, с которой следует рассчитывать математическую модель. Нет смысла решать задачу существенно точнее, чем это диктуется неопределенностью исходных данных. Таким образом, погрешность метода подчиняют погрешности задачи. Наконец, при выводе оценок погрешностей численных методов обычно исходят из предположения, что все операции над числами выполняются точно. Это означает, что погрешность округлений не должна существенно отражаться на результатах реализации методов, т.е. должна подчиняться погрешности метода. Влияние погрешностей округлений не следует упускать из вида ни на стадии отбора и алгоритмизации численных методов, ни при выборе вычислительных и программных средств, ни при выполнении отдельных действий и вычислении значений функций.

Пример. Пусть требуется вычислить площадь фигуры, ограниченной некоторой кривой, отрезками прямых и осью ординат.

Пусть S – это истинное значение площади рассматриваемой фигуры. В качестве математической модели для вычисления площади возьмем интеграл 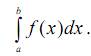Неточность в этом выражении заложена в числах a и b и в функции 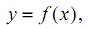которая аппроксимирует криволинейную границу области. Пусть 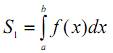– истинное значение интеграла. Тогда разность 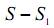и будет неустранимой погрешностью модели. Для вычисления интеграла применим численный метод, допустим некоторую интегральную сумму .

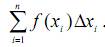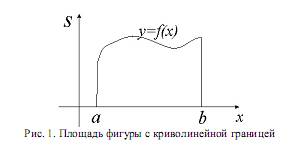
Рис. 1. Площадь фигуры с криволинейной границей

Пусть S₂ – истинное значение суммы. Разность S₁ - S₂ – это погрешность численного метода. Пусть, наконец, S₃ – тот результат, который получился после вычисления суммы. Из-за округлений получим величину, вообще говоря, отличающуюся от S₂. Разность S₂ – S₃ – это вычислительная погрешность. Сумма трех указанных погрешностей, которая равна разности S – S₃ , т.е. разности между истинным значением площади (неизвестным нам) и тем значением, которое мы выдаем в качестве решения задачи, и есть полная погрешность.

Некоторые алгоритмы весьма чувствительны к ошибкам округлений. При счете по таким алгоритмам небольшая погрешность, допущенная на каком-либо его шаге, может сильно нарастать и в результате получится весьма большая вычислительная погрешность. Такие алгоритмы называют неустойчивыми.

Вычислительными называются погрешности, которые образуются в следствии необходимости выполнять арифметические операции над приближенными числами, вычислять значения функций, а также округлять исходные данные, промежуточные и окончательные результаты. При этом оказывается, что погрешность результата любого арифметического действия, как правило, превышает погрешности исходных данных.

Определенное влияние на результаты оказывает и степень точности используемых средств вычислений. Для представления чисел в них выделяется ограниченное количество десятичных разрядов, что влечет автоматическое округление числовых данных. Чем больше разрядная сетка, тем погрешность округлений меньше и, следовательно, с тем большей точностью можно производить вычисления. Часто, после выполнения операции производится не округление результата, а простое отбрасывание лишних разрядов с целью экономии машинного времени. Правда, в современных машинах предусмотрена свобода выбора программистом способа округления; соответствующими средствами располагают большинство алгоритмических языков.

Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2), Это может привести к тому, что в новой системе счисления число становится иррациональным.

Например, число 0.1 при переводе в двоичную систему счисления примет вид 0.1 = 0.00011001100... Может оказаться, что если с шагом 0.1 нужно при вычислениях пройти отрезок [0, 1] от х = 1 до х = 0, то десять шагов не дадут точного значения х = 0.

Несмотря на то, что при решении больших задач выполняются миллиарды операций, это вовсе не означает механического умножения погрешности при одном округлении на число операций, так как при отдельных действиях погрешности могут компенсировать друг друга (например, при сложении чисел разных знаков). Вместе с тем, иногда погрешности округлений в сочетании с плохо организованным алгоритмом могут сильно исказить результаты.

Понятие погрешности.

Различают два вида погрешностей - абсолютную и относительную. Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения. Относительная погрешность - это отношение абсолютной погрешности к истинному значению числа.

Абсолютной погрешностью приближенного числа а назовем величину ∆а, про которую известно, что .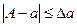

Таким образом, точное число заключено в границах 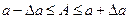или сокращенно .

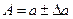Пример. Приближенные числа а₁=2,87; а₂=300; а₃=3*10² получены округлением, точные значения чисел неизвестны. Что можно сказать об абсолютной погрешности данных приближенных чисел?

Решение. Пользуясь правилами округления чисел, можно сказать, что абсолютные погрешности приближенных чисел не превосходят половины единицы последнего разряда, т.е.

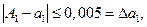
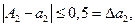
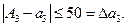
Для приближенного числа, полученного в результате округления, абсолютная погрешность ∆a принимается равной половине единицы последнего разряда числа.

Пример. Значение а=0,734 могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом ∆a≤0,0005, и полагаем ∆a=0,0005.

При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления.

Абсолютная погрешность связана с размерностью и не полностью характеризует результат. Например, известно, что абсолютная погрешность равна 3 см. Ясно, что имеем совершенно различный по точности результат, если речь идет о длине карандаша или о расстоянии между Землей и Сатурном. Поэтому вводят понятие относительной погрешности.

Относительной погрешностью δа приближенного числа а называется отношение абсолютной погрешности ∆а к абсолютной величине приближенного числа а: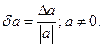

Для приближенного числа, полученного в результате округления, абсолютная погрешность ∆a принимается равной половине единицы последнего разряда числа. Например, значение а=0.734 могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом ∆a≤0.0005, и полагаем ∆a=0.0005.

Приведем примеры оценки абсолютной погрешности при некоторых значениях приближенной величины а.

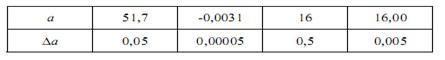
При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления.

Например: относительная погрешность δ(-2.3) = 0.05/2.3 ≈ 0.022 (2.2%). Заметим, что погрешность округляется всегда в сторону увеличения. В данном случае δ(-2.3) ≈ 0.03.

Определение. Значащими цифрами в десятичной записи числа называются все цифры, начиная с первой ненулевой слева.

Определение. Значащая цифра называется верной в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Определение. Значащая цифра называется верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Сформулируем правила округления:

1. если отбрасываемые при округлении цифры составляют число, большее половины единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу;

2. если отбрасываемые при округлении цифры составляют число, меньшее половины единицы последнего оставляемого разряда, то оставляемые цифры остаются без изменения;

3. при округлении, когда отбрасываемые цифры составляют число, равное половине единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остается без изменения, если она четная (правило четной цифры).