Значение числа «3» в естественных науках

Введение

С незапамятных времен числа используются в повседневной жизни. В более позднее время они стали применяться в торговле, на производстве, в науке и технике. Число является одним из основных понятий математики. Они служат для описания и исследования количественных отношений, позволяют выразить результаты счета или измерений. Понятие числа служит исходным для многих математических теорий. Числа находят широкое применение в физике, механике, астрономии, химии, географии и других науках.

Основателем мистического учения о числах стал знаменитый древнегреческий философ VI века до н.э. Пифагор. Он и его последователи считали, что все в природе измеряется, подчиняется числу и познать мир – это значит познать управляющие им числа.

Современные люди широко применяют в своей жизни числа. Мы их используем, чтобы измерить время, купить, продать, позвонить, посмотреть телевизор. К тому же у каждого человека есть различные числа, подтверждающие его личность: в паспорте, в кредитной карточке, в свидетельстве о рождении и т.д.

Вряд ли сейчас кто-нибудь вкладывает в числа сказочный или мифический смысл. Но так было не всегда. Для древних людей числа были элементами особого кода, с помощью которого описывался мир человека. Во многих древних культурах числовой ряд открывало число «3».В далекие времена люди с большим трудом научились считать сначала до двух и только через много – много лет начали продвигаться в счете. Каждый раз за двойкой начиналось что-то неизвестное, загадочное. Когда считали «один, два, много», то после двух было «всё». Поэтому число три, которое при счёте должно было идти за числом два, обозначало «всё».

В своей работе мы попытались найти ответы на вопросы что же это такое «всё», то есть «тройка», какое значение это число играет в разных областях нашей жизни, разгадать хотя бы некоторые его тайны.

Значение числа «3» в естественных науках

В этом разделе я хотел бы рассказать о месте и значении «3» в области естественных дисциплин.

Число 3 сравнивается пифагорейцами с мудростью, потому что люди организуют настоящее, предвидят будущее и используют опыт прошлого. Пифагорейцы считали, что число 3(триада) - это первое равновесие единиц, это первое число, которое по- настоящему нечетно. Триада есть число познания музыки, геометрии, астрономии и науки о небесных и земных телах.

Пифагор учил, что триада - священное число, потому что она создается из монады (Божественного Отца) и дуады (Великой Матери). Древний философ говорил также, что все в природе разделено на три части, и, что никто не может стать воистину мудрым, пока не будет представлять каждую проблему в виде треугольной диаграммы.

Мне пришлось много «покапаться» в интернете и найти, где применяется число 3, в каких областях науки. Многое, конечно, я не понял, потому что не изучал эти области, но со временем я разберусь.

Математика

В математике тройка «3» одна из десяти цифр, используемых для записи чисел в десятичной системе счисления.

Числа, в записи которых используется цифра «3»

1/3 - треть

3 - три

13 - тринадцать

23 – двадцать три

30 - тридцать

38 тридцать восемь

300 - триста

333 – триста тридцать три и многие др.

Число «3» (три) является третьим натуральным числом, расположенным в ряде натуральных чисел между «2» и «4».

Число «3» - второе простое число.

В интернете вычитал, что:

Число «3» является элементом некоторых числовых последовательностей.

«3» - пятый элемент в последовательности чисел Фибоначчи. Числа Фибоначчи – элементы числовой последовательности: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …, в которой каждое последующее число равно сумме двух предыдущих чисел.

Свое название числа получили по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи). Более формально, последовательность чисел Фибоначчи {F_n} задается линейным рекуррентным соотношением:

F₀=0, F₁=1, F_n=F_n-1+F_n-2.

Иногда число 0 не рассматривается как член последовательности. Числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: F_n=F_n+2−F_n+1.

«3» - нулевой элемент последовательности чисел Ферма. Числа Ферма – это числа вида (2 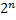+1), где n - неотрицательное целое число. Последовательность чисел Ферма начинается так: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, …

«3» - второй элемент последовательности чисел Мерсенна. Числа Мерсенна – это числа вида M_n=2n−1, где n - натуральное число. Последовательность чисел Мерсенна начинается так: 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, …

«3» - второе число Софи Жермен. В теории чисел простое число Софи Жермен - это такое простое число p, что число 2p + 1 также является простым. Так 3·2+1=7, а число 7 является простым. Последовательность чисел Софи Жермен начинается так: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359 ...

Предполагается, что количество простых чисел Софи Жермен бесконечно, но это не доказано.

«3» относиться к фигурным числам (второе треугольное число). Фигурные числа - общее название чисел, связанных с той или иной геометрической фигурой. Это историческое понятие восходит к пифагорейцам. Предположительно от фигурных чисел возникло выражение: «Возвести число в квадрат или в куб».

«3»-целое приближение числа π (произносится «пи») - математическая константа, выражающая отношение длины окружности к длине её диаметра.

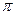≈ 3,1415926535897932384626433832795…;

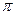≈ 3.

«3»-целое приближение иррационального числа .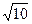

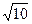≈ 3,1622776601683793319988935444327…;

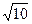≈ 3.

Три играет роль в приставках международной системы единиц СИ (Система Интернациональная):

10³ кило (к) – километр (км), килограмм (кг), киловатт (кВт) и др.;

10⁻³ милли (м) – миллиграмм(мг), миллиметр (мм), миллилитр(мл) и др.

Приставки СИ (десятичные приставки) - приставки перед названиями или обозначениями единиц измерения физических величин. Применяются для формирования кратных и дольных единиц, отличающихся от базовой единицы в определённое целое число раз, являющееся степенью числа 10. Десятичные приставки служат для сокращения количества нулей в численных значениях физических величин.

«Три» в формулировках математических правил и пояснениях

Аксиома геометрии

«Через любые три точки, не лежащие на одной прямой, можно провести только одну плоскость».

Определения и пояснения:

Треугольник - многоугольник с тремя вершинами.

Трёхмерное пространство - геометрическая модель материального мира, в котором мы находимся.

Трисекция угла - задача о делении заданного угла на три равные части с помощью циркуля и линейки. Иначе говоря, необходимо построить трисектрисы угла - лучи, делящие угол на три равные части.

Химия

География

Физика

Содержание физики может быть разделено на три части. К первой части можно отнести явления качественного характера, ко второй – законы количественные, к третьей – объяснения явлений.

Положение тела в пространстве характеризуется тремя числами – координатами тела.

Три закона Ньютона, сформулированные им в 1687 г. и лежащие в основе так называемой, классической механики.

Первый закон: "Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние".

Второй закон: "Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует".

Третий закон: "Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны".

Три состояния вещества: твердое, жидкое и газообразное.

Цвета цифры 3

Для цифры 3 характерны кроваво-красный, янтарный, рубиновый и розовый цвета.

Число 3 в музыке

Число 3 также имеет большое распространение в музыке. Если зайти на один из русских сайтов, посвященных музыке, и попытаться найти исполнителя или аудиокомпозицию, в названии которой будет число 3, то мы получим интересные сведения:

По запросу «3» найдено:

136 исполнителей

4250 альбомов

78729 аудиокомпозиций.

Например:

«3» — музыкальная рок-группа из города Вудсток.

«3» — третий альбом американо-бразильской группы Soulfly.

«3» — первый сингл американской певицы Бритни Спирс.

«3» — альбом французской группы Nouvelle Vague.

«3» — альбом русского рэпера Баста.

Таким образом, число 3 выполняет не только информативную роль, но и экспрессивную функцию. Число 3 оказывается «движущей пружиной» музыки.

Число 3 у народов мира

Тройка. У многих народов весьма продолжительное время пределом счета было число 3. Его считали символом полноты, совершенства. Так, у древних греков это число считалось счастливым, а в Древнем Вавилоне стали поклоняться трем божествам: Солнцу, Луне и Венере. Число три стало самым излюбленным числом и в мифах, и в сказках. Еще его магия заключалась в том, что оно складывалось из суммы предыдущих чисел (3=1+2), символизировалось треугольником, который представляет прошлое, настоящее и будущее.

Число «3» - это одно из священных чисел у многих народов как в материальной, так ив духовной культуре, это знак Земли. Это также идеальная модель любого динамического процесса, предполагающая возникновение (зарождение), развитие и упадок (кончина, смерть): все в мире появляется, зарождается, живет и развивается, но нет ничего вечного на Земле - все умирает, стареет, все приходит в упадок. Числом три выражается вертикальная модель мира, верх, середина, низ - Небо, Земля, преисподняя - Рай, земной мир, ад. Цифрой «3» выражается понятие временного характера: прошлое, настоящее, будущее - три языка пламени в эмблеме Бурятии. Цифра «3» считается священным, так как символизирует треугольник, олицетворяющий Святую троицу - разум, тело и дух, или мать, отца и ребенка. Выражение «бог троицу любит» не случайное, многие народы любят его и считают «3» счастливым числом. 3 фазы Луны (первая четверть, полнолуние и новолуние) ассоциируются с фазами в жизни женщины - девушка, мать и пожилая женщина. Как планета женского рода, она влияет на женские эмоции и материнство. Тройка очень часто встречается в фольклорных жанрах многих народов. Герой произведения обычно совершает 3 разных подвига, женихи подвергаются 3 - кратным испытаниям; обычно в семье растут 3 сына и 3 дочери, путь, по которым проезжают герои, - на развилке трех дорог, чудеса происходят во всех трех мирах; об очень счастливом моменте говорят «трижды счастлив», за тридевять земель, в тридесятом царстве - государстве», на тройке лошадей совершают свое путешествие небесные и земные герои. Таких примеров много. Представления о верхнем, среднем, нижнем мирах, о прошлом, настоящем и будущем времени - универсальные понятия в мифологии, позднее - в фольклоре, героическом эпосе.

В бурятском, монгольском фольклоре до сих пор бытует жанр триады. Триады представляют собой поэтический афоризм, в котором заложена определенная информация, сгруппированная по признакам (цветовому, внешнему, нравственному).

Триада - своеобразная, оригинальная загадка. Вопрос задается в краткой традиционной форме: «Что в мире три быстрых, трудных, далеких». На это отвечают стихами, состоящими из 3 или 4 строк. Например, «Что в мире 3 богатых», отвечают «Земля богата корнями, небо богато звездами, океан богат водой». Триада может быть и в форме поговорки: «Три богатства есть в мире: богат тот, у кого скота много; еще богаче тот, у кого детей много; но богаче всех тот, кто знанием богат»; «Три вещи в мире опасны: нож в руках ребенка, власть в руках глупца, лесть в устах подхалима». Триады могут иметь много вариантов вопросов и ответов. Легкий, игровой фольклорный жанр выступает как средство осмысления и познания окружающего мира. Они передаются из поколения в поколение, дополняясь новыми понятиями в зависимости от интеллекта, эрудиции, сообразительности, наблюдательности исполнителя. У бурят бытует более 40 разных триад типа: 3 белых, 3 красных, 3 синих , 3 желтых , 3 черных, 3 зеленых, 3 опрятных, 3 пустых, 3 гордых, 3 далеких, 3 бездонных, 3 неспокойных.

Число 3 в древних культурах

Основателем мистического учения о числах стал знаменитый древнегреческий философ VI века до н.э. Пифагор. Он и его последователи считали, что все в природе измеряется, подчиняется числу и познать мир – это значит познать управляющие им числа.

Во многих древних культурах числовой ряд открывало число «3», часто означающее абсолютное совершенство.

Число три считалось в древности магическим, потому что оно складывалось из суммы двух предыдущих (3 = 2 + 1), символизировало треугольник, который представляет прошлое, настоящее и будущее.

Число три стало самым излюбленным числом и в мифах, и в сказках. Цифра три часто встречается в пословицах, поговорках, дразнилках, считалках, скороговорках.

Самым распространенным числительным в сказках Пушкина является число 3.

Число «3» часто встречается в русских народных сказках. Цифра «3» в сказках наталкивает читателя на мысль о волшебстве, о совершенстве. Ведь в русских сказках всегда желания исполняются только в третий раз.

Число 3 в образовании

Тривиум (трёхпутье) — начальный курс семи свободных искусств в средневековых университетах, включавший три учебные дисциплины.

«3» (тройка) — оценка, означающая «удовлетворительно».

Заключение

Цифра три невелика, но без нее жить невозможно.

3 есть в светофоре, запрягают 3 лошадей, в сказках не обошлись без 3, на картине Васнецова «Три богатыря» мы ее видим снова.

Практически нет раздела науки и техники, искусства и литературы, в котором бы не использовалось число 3. Оно поистине священное и загадочное. Единственное место, где не любят число 3- это школа, все хотят получать только 5.

Тройка – первое совершенное, сильное число, поскольку при его разделении сохраняется центр, то есть центральная точка равновесия. Оно является янским и благоприятным.

Тройка означает также исполнение, часто воспринимается как знак удачи: возможно, потому, что означает выход из противостояния – решающее действие, которое может, однако, привести и к неудаче.

В пифагорействе тройка символизирует полноту. Пифагор считал тройку символом гармонии, а Аристотель – законченности: «Триада есть число целого, ибо содержит начало, середину и конец». Пифагорейцы различали три мира как вместилища принципов, разума и количеств.

Тройка несет в себе уверенность и силу, так как если один или два раза могут быть совпадением, то три раза – это уже закономерность.

Три также самое меньшее количество, составляющее родовую общину, маленькое – наименьшее количество людей, имеющих право принимать сколь – либо значимые решения, как, например, триумвират в Древнем Риме.

Сам человек обладает тройной организацией, заключая в себе тело, душу и дух.

Три – одно из самых положительных чисел не только в символике и религиозной мысли, но и в мифологии, легендах и сказках, где примета «третий раз – удачный» имеет очень древние корни. В народных сказках герои обычно имеют три желания, а и исполняются на третий раз: надо выдержать три испытания или три попытки, что бы добиться благоприятного результата. В фольклоре встречаются три царевича, три ведьмы, феи (две добрые, одна злая).

Тройка – первое совершенное, сильное число, поскольку при его разделении сохраняется центр, то есть центральная точка равновесия. Оно является янским и благоприятным.

Тройка означает также исполнение, часто воспринимается как знак удачи: возможно, потому, что означает выход из противостояния – решающее действие, которое может, однако, привести и к неудаче.

И мы рады, что так близко познакомились с числом 3 и познакомили вас с ним.

Так давайте же верить в мистическое начало числа 3 и умело применять его к своей жизни, тогда все в нашей жизни будет гармонично. А гармония – залог успеха и процветания.

Приложение1

Число 3 в других областях

3 — шифр немецкого языка в международном коде книг — ISBN.

Формат A3.

В каждом квартале и каждом времени года по 3 месяца.

Трезубец.

Тройка лошадей.

«3» — музыкальная группа.

3 составляющих части марксизма — английская политэкономия,

французский социализм, германская философия.

3 знака тире — дефис, минус/кортире, тире.

В спортивных индивидуальных дисциплинах даются три попытки.

Трёхфазная система переменного тока в электротехнике.

Троичный триггер в электронике.

Триколор — трёхцветный флаг.

Тройной прыжок в спорте.

Тройник в электротехнике.

Тройной одеколон в парфюмерии.

Третий день недели — среда.

Третий месяц года — март.

Трёхлинейка — народное название винтовки Мосина.

Треух — разновидность зимней шапки с тремя «ушами».

Триод — электронная лампа с тремя электродами.

Тройная уха в кулинарии.

Три короны на гербе России и Швеции.

Триплекс — трёхслойное стекло.

Треножник — подставка на трёх ногах.

Тройничный нерв — в анатомии человека.

Тримаран — судно с тремя корпусами.

Трилобит — вымершее существо с панцирем из трёх частей.

Трёхгранный русский штык.

Триплан — разновидность самолёта.

Трёхстворчатый клапан сердца.

Жёлтый — третий цвет радуги.

Треуголка — шляпа.

Письма-треугольники.

Три копейки — монета времён царской России и СССР.

Три рубля — денежные единицы времён царской России и СССР.

Трёшник — 3 рубля в СССР с 1961 г.

Трояк — оценка 3 в учебных заведениях, 3 рубля в СССР с 1961 г.

Стреноженный конь.

Трёхлитровая стеклянная банка.

Три календарных месяца в квартале, сезоне.

Терция в музыке.

Третьяков, Третьяк — фамилии.

Третник — мягкий припой из трёх металлов.

МиГ-3 и Як-3 — советские истребители времён второй мировой войны.

ИС-3 — советский тяжёлый танк периода Великой Отечественной войны.

Три базовых цвета при синтезе изображений: в аддитивной цветовой модели красный, зелёный и синий (RGB), в субстрактивной модели голубой, пурпурный и жёлтый (CMY).

Приложение2

Число индивидуальности

В обследовании участвовало 23 одноклассника, для которых было вычислено число индивидуальности, равное сумме числа имени и числа даты рождения.

Результаты обследования показаны в таблице 1.

Таблица 1.

Число индивидуальности	Количество учащихся

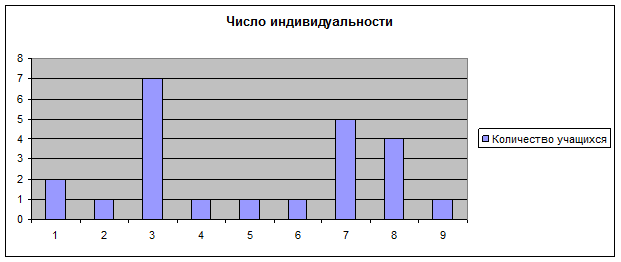
Из таблицы видно, что больше всего учащихся (7 человек) имеют число индивидуальности 3.

Тройка в номерах телефонов

Было обследовано 26 номеров сотовых телефонов родителей учащихся 7а класса, из них у 14 человек в номерах телефонов встречается тройка, причем дважды она встречается у 4 человек, трижды – у 1 человека.

Введение

С незапамятных времен числа используются в повседневной жизни. В более позднее время они стали применяться в торговле, на производстве, в науке и технике. Число является одним из основных понятий математики. Они служат для описания и исследования количественных отношений, позволяют выразить результаты счета или измерений. Понятие числа служит исходным для многих математических теорий. Числа находят широкое применение в физике, механике, астрономии, химии, географии и других науках.

Основателем мистического учения о числах стал знаменитый древнегреческий философ VI века до н.э. Пифагор. Он и его последователи считали, что все в природе измеряется, подчиняется числу и познать мир – это значит познать управляющие им числа.

Современные люди широко применяют в своей жизни числа. Мы их используем, чтобы измерить время, купить, продать, позвонить, посмотреть телевизор. К тому же у каждого человека есть различные числа, подтверждающие его личность: в паспорте, в кредитной карточке, в свидетельстве о рождении и т.д.

Вряд ли сейчас кто-нибудь вкладывает в числа сказочный или мифический смысл. Но так было не всегда. Для древних людей числа были элементами особого кода, с помощью которого описывался мир человека. Во многих древних культурах числовой ряд открывало число «3».В далекие времена люди с большим трудом научились считать сначала до двух и только через много – много лет начали продвигаться в счете. Каждый раз за двойкой начиналось что-то неизвестное, загадочное. Когда считали «один, два, много», то после двух было «всё». Поэтому число три, которое при счёте должно было идти за числом два, обозначало «всё».

В своей работе мы попытались найти ответы на вопросы что же это такое «всё», то есть «тройка», какое значение это число играет в разных областях нашей жизни, разгадать хотя бы некоторые его тайны.

Значение числа «3» в естественных науках

В этом разделе я хотел бы рассказать о месте и значении «3» в области естественных дисциплин.

Число 3 сравнивается пифагорейцами с мудростью, потому что люди организуют настоящее, предвидят будущее и используют опыт прошлого. Пифагорейцы считали, что число 3(триада) - это первое равновесие единиц, это первое число, которое по- настоящему нечетно. Триада есть число познания музыки, геометрии, астрономии и науки о небесных и земных телах.

Пифагор учил, что триада - священное число, потому что она создается из монады (Божественного Отца) и дуады (Великой Матери). Древний философ говорил также, что все в природе разделено на три части, и, что никто не может стать воистину мудрым, пока не будет представлять каждую проблему в виде треугольной диаграммы.

Мне пришлось много «покапаться» в интернете и найти, где применяется число 3, в каких областях науки. Многое, конечно, я не понял, потому что не изучал эти области, но со временем я разберусь.

Математика

В математике тройка «3» одна из десяти цифр, используемых для записи чисел в десятичной системе счисления.

Числа, в записи которых используется цифра «3»

1/3 - треть

3 - три

13 - тринадцать

23 – двадцать три

30 - тридцать

38 тридцать восемь

300 - триста

333 – триста тридцать три и многие др.

Число «3» (три) является третьим натуральным числом, расположенным в ряде натуральных чисел между «2» и «4».

Число «3» - второе простое число.

В интернете вычитал, что:

Число «3» является элементом некоторых числовых последовательностей.

«3» - пятый элемент в последовательности чисел Фибоначчи. Числа Фибоначчи – элементы числовой последовательности: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …, в которой каждое последующее число равно сумме двух предыдущих чисел.

Свое название числа получили по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи). Более формально, последовательность чисел Фибоначчи {F_n} задается линейным рекуррентным соотношением:

F₀=0, F₁=1, F_n=F_n-1+F_n-2.

Иногда число 0 не рассматривается как член последовательности. Числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: F_n=F_n+2−F_n+1.

«3» - нулевой элемент последовательности чисел Ферма. Числа Ферма – это числа вида (2 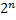+1), где n - неотрицательное целое число. Последовательность чисел Ферма начинается так: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, …

«3» - второй элемент последовательности чисел Мерсенна. Числа Мерсенна – это числа вида M_n=2n−1, где n - натуральное число. Последовательность чисел Мерсенна начинается так: 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, …

«3» - второе число Софи Жермен. В теории чисел простое число Софи Жермен - это такое простое число p, что число 2p + 1 также является простым. Так 3·2+1=7, а число 7 является простым. Последовательность чисел Софи Жермен начинается так: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359 ...

Предполагается, что количество простых чисел Софи Жермен бесконечно, но это не доказано.

«3» относиться к фигурным числам (второе треугольное число). Фигурные числа - общее название чисел, связанных с той или иной геометрической фигурой. Это историческое понятие восходит к пифагорейцам. Предположительно от фигурных чисел возникло выражение: «Возвести число в квадрат или в куб».

«3»-целое приближение числа π (произносится «пи») - математическая константа, выражающая отношение длины окружности к длине её диаметра.

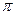≈ 3,1415926535897932384626433832795…;

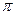≈ 3.

«3»-целое приближение иррационального числа .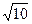

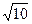≈ 3,1622776601683793319988935444327…;

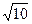≈ 3.

Три играет роль в приставках международной системы единиц СИ (Система Интернациональная):

10³ кило (к) – километр (км), килограмм (кг), киловатт (кВт) и др.;

10⁻³ милли (м) – миллиграмм(мг), миллиметр (мм), миллилитр(мл) и др.

Приставки СИ (десятичные приставки) - приставки перед названиями или обозначениями единиц измерения физических величин. Применяются для формирования кратных и дольных единиц, отличающихся от базовой единицы в определённое целое число раз, являющееся степенью числа 10. Десятичные приставки служат для сокращения количества нулей в численных значениях физических величин.

«Три» в формулировках математических правил и пояснениях