Методические указания по написанию реферата.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
"МУРМАНСКИЙ АРКТИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ" (ФГБОУ ВО "МАГУ")
Филиал МАГУ в г. Кировске
| СОГЛАСОВАНО Зам. директора филиала по УиВР _____________ В.А. Ганичева "" 20г. | УТВЕРЖДАЮ Директор филиала __________А.А. Разумовская "" 20г. | |
| СОГЛАСОВАНО Ведущий специалист по УМР _____________ Е.А. Ярославцева "" 20г. |
ЗАДАНИЯ
для внеаудиторной самостоятельной работы студентов
по учебной дисциплине ЕН.01. Элементы высшей математики
для специальности 09.02.03 Программирование в компьютерных системах
Преподаватель: ___________ Орлова О.А.
Рекомендован к утверждению на заседании цикловой комиссии:
Протокол №_____от «____» __________ 201__ г.
Председатель цикловой комиссии _______________ Котович Е.А.
Кировск
2016
СОДЕРЖАНИЕ
Введение. 3
1. Задания для внеаудиторной (домашней) самостоятельной работы по учебной дисциплине ЕН.03. Теория вероятностей и математическая статистика. 5
2. Общие методические рекомендации различных видов внеаудиторной самостоятельной работы. 13
2.1. Методические указания по написанию реферата. 13
2.2. Методические указания по подготовке мультимедийных презентаций. 14
2.3. Методические указания по решению задач и упражнений. 16
2.4. Методические указания по выполнению заданий с привлечением информационных технологий. 17
3. Рекомендуемая литература для выполнения внеаудиторной (домашней) самостоятельной работы. 18
Приложение 1. Темы для выполнения реферата и мультимедийной презентации. 19
Приложение 2. График защиты рефератов и мультимедийных презентаций. 20
Введение.
Требованиями образовательной программы предусмотрено обязательное выполнение обучающимися по каждой учебной дисциплине определенного объема внеаудиторной самостоятельной работы.
В ходе изучения дисциплины ЕН.01. Элементы высшей математики предусмотрена внеаудиторная (домашняя) самостоятельная работав объеме 50 часов.
Наличие положительной оценки каждого задания внеаудиторной самостоятельной работы необходимо для получения зачета по дисциплине и допуска к экзамену, поэтому в случае невыполнения работы по любой причине или получения неудовлетворительной оценки за самостоятельную работу вы должны найти время для ее выполнения и пересдачи.
Домашнее задание выполняется студентами в целях:
- развитие общих и профессиональных компетенций;
- углубление и расширение теоретических знаний;
- формирование умений использовать справочную и специальную литературу;
- развитие познавательных способностей и активности обучающихся;
- формирование самостоятельности мышления, способностей к саморазвитию, совершенствованию и самоорганизации;
- умение использовать материал, собранный и полученный в ходе самостоятельных занятий для эффективной подготовки к экзамену.
Внеаудиторная самостоятельная работа дополняет содержание аудиторных занятий, способствует закреплению, обобщению и систематизации полученных на уроках теоретических знаний и совершенствованию практических умений, а также развитию таких качеств личности, как ответственность и организованность.
Объем времени для выполнения учебного задания определен эмпирически на основании наблюдений за выполнением студентами аудиторной самостоятельной работы; опроса студентов о затратах времени на выполнение того или иного внеаудиторного задания; хронометража собственных затрат на решение той или иной задачи с внесением поправочного коэффициента из расчета уровня знаний и умений студентов по дисциплине.
Домашнее задание по элементам высшей математики состоит из следующих видов работ:
1) написание рефератов;
2) создание мультимедийных презентаций;
3) решение задач и упражнений;
4) выполнение заданий с привлечением информационных технологий.
Формами контроля по написанию рефератов и созданию мультимедийных презентаций является защита реферата и представление презентации. Письменное решение задач и упражнений выполняется в отдельной тетради для самостоятельных работ и сдается преподавателю. Формой контроля является просмотр и проверка выполнения домашнего задания. Задания с привлечением информационных технологий выполняются на компьютере и сдаются преподавателю в электронном виде. Формой контроля по выполнению заданий с привлечением информационных технологий является просмотр и проверка выполнения домашнего задания.
Для каждого вида внеаудиторной самостоятельной работы ниже приведены методические указания по выполнению.
Обратите внимание, что все виды заданий для внеаудиторной самостоятельной работы представлены в таблице, там же указан примерный объем времени на выполнение задания. Таблица будет являться вашим ориентиром в выполнении домашней работы.
Оценка за выполнение домашнего задания выставляется в журнал учебных занятий.
Уважаемый студент!
| Желаем удачи! |
| Ознакомьтесь с таблицей заданий внеаудиторной (домашней) самостоятельной работы и перечнем рекомендуемой литературы |
| Прежде чем приступить к выполнению внеаудиторной самостоятельной работы, прочтите Введение |
| Прочтите методические указания по выполнению некоторых заданий внеаудиторной самостоятельной работы |
| Выполните задание |
| Упражнения и задачи должны быть выполнены к следующему учебному занятию, реферат и презентация выполняется в соответствии с графиком (приложение 2) |
| Если у вас возникнут затруднения в процессе работы, обратитесь к преподавателю |
1. Задания для внеаудиторной (домашней) самостоятельной работы по учебной дисциплине ЕН.03. Теория вероятностей и математическая статистика
Таблица
| № дом. задания | Номер и наименование разделов, тем | Задания для внеаудиторной (домашней) самостоятельной работы | Примерный объем времени на выполнение, в час. |
| 1. | Из предложенной тематики (приложение 1) выбрать одну тему. По этой теме подготовить реферат и создать к нему мультимедийную презентацию. | ||
| Раздел 1. Элементы линейной алгебры. | |||
| 2. | Тема 1.1. Матрицы и действия над ними. | Решить упражнение № 1. 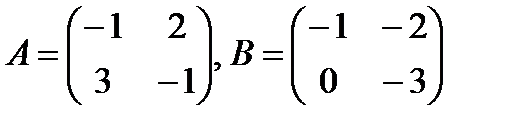 . Найти Ат-3В. Решить упражнение № 2. Найдите произведение матриц: а) . Найти Ат-3В. Решить упражнение № 2. Найдите произведение матриц: а) 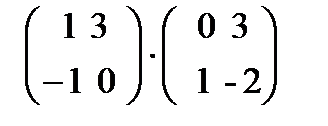 , б) , б) 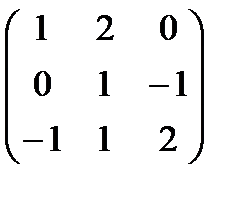 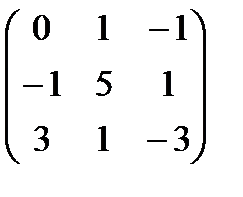 . . | |
| 3. | Тема 1.2. Определитель матрицы и его свойства. | Решить упражнение № 1. Вычислите определители: 1) 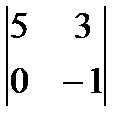 ; 2) ; 2) 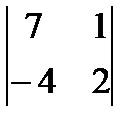 ; 3) ; 3) 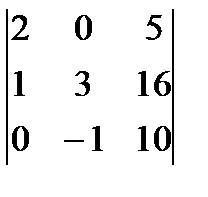 ; 4) ; 4) 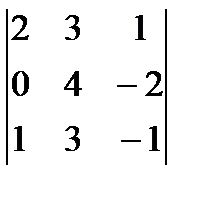 . . | |
| 4. | Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Вычислить определитель второго, третьего, четвертого, пятого и десятого порядка. При введении исходных данных, результат должен вычисляться автоматически. | ||
| 5. | Тема 1.3. Обратная матрица. Ранг матрицы. | Решить упражнение № 1. Найдите матрицу, обратную данной: 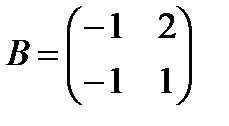 . . | |
| 6. | Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Найдите матрицу, обратную данной: 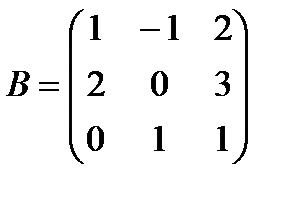 . При введении исходных данных, результат должен вычисляться автоматически. . При введении исходных данных, результат должен вычисляться автоматически. | ||
| Раздел 2.Системы линейных уравнений и методы их решения. | |||
| 7. | Тема 2.1.СЛАУ, общее решение. Частное и базисное решение. | Решить упражнение № 1. Решите системы линейных уравнений: 1) 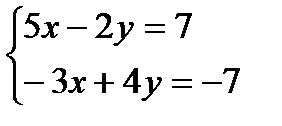 ; 2) ; 2) 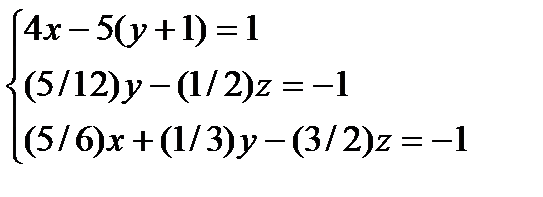 . . | |
| 8. | Тема 2.2. Решение СЛАУ методом Крамера и матричным методом. | Решить упражнение № 1. Решите систему линейных уравнений по правилу Крамера и матричным методом: 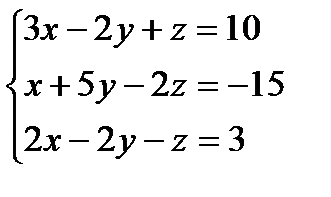 . . | |
| 9. | Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Решите системы линейных уравнений методом обратной матрицы и методом Крамера: 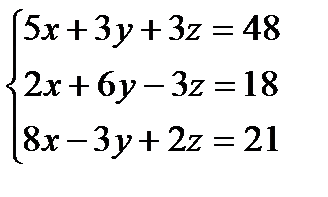 При введении исходных данных, результат должен вычисляться автоматически. При введении исходных данных, результат должен вычисляться автоматически. | ||
| 10. | Тема 2.3. Решение СЛАУ методом Гаусса. | Решить упражнение № 1. Решите систему линейных уравнений методом Гаусса: 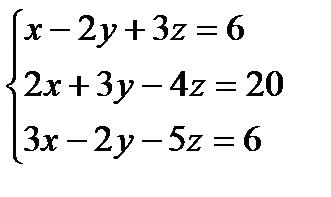 . . | |
| 11. | Решение СЛАУ методом Гаусса. Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Решите систему линейных уравнений методом Гаусса: 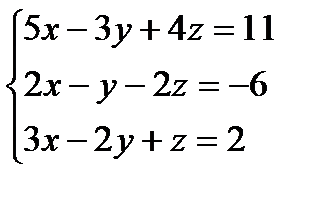 . При введении исходных данных, результат должен вычисляться автоматически. . При введении исходных данных, результат должен вычисляться автоматически. | ||
| Раздел 3. Элементы аналитической геометрии. | |||
| 12. | Тема 3.1. Векторы. Операции над векторами. | Решить задачу № 1.  Решить задачу № 2. Решить задачу № 2. 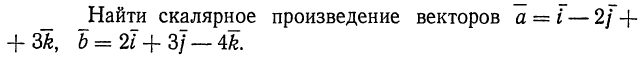 | 0,5 |
| 13. | Решить задачу № 1. 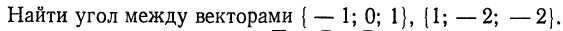 | 0,5 | |
| 14. | Тема 3.2. Уравнение прямой на плоскости. | Решить задачу № 1. 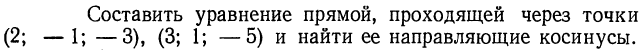 | |
| 15. | Тема 3.3. Кривые второго порядка. | Решить задачу № 1.  Решить задачу № 2. Решить задачу № 2. 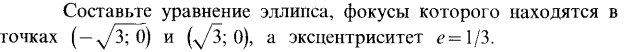 | |
| 16. | Решить задачу № 1. 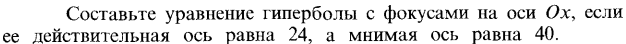 Решить задачу № 2. Решить задачу № 2. 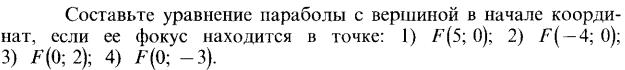 | 0,5 | |
| 17. | Решить задачу № 1.  | 0,5 | |
| Раздел 4. Основы теории комплексных чисел. | |||
| 18. | Тема 4.1. Комплексные числа, действия над ними. | Решить упражнение № 1. Найдите модуль и главное значение аргумента комплексных чисел: 1) -3i; 2) -2-2i; 3) 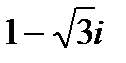 . Решить упражнение № 2. Даны числа z1 и z2. Найдите . Решить упражнение № 2. Даны числа z1 и z2. Найдите 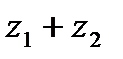 , , 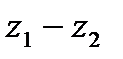 , , 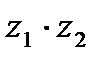 , , 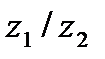 . 1) . 1) 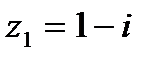 и и 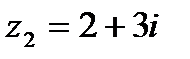 ; 2) . ; 2) . 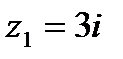 и и 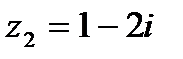 | |
| 19. | Решить упражнение № 1. Представьте в тригонометрической форме комплексные числа: 1) 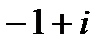 ; 2) ; 2) 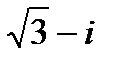 . Решить упражнение № 2. Выполните действия: 1) . Решить упражнение № 2. Выполните действия: 1) 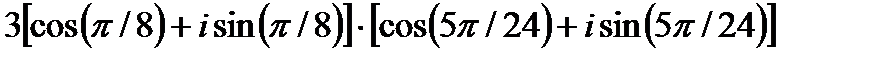 ; 2) ; 2) 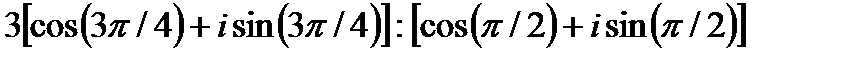 . . | 0,5 | |
| 20. | Решить упражнение № 1. Вычислите: 1) 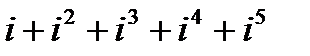 , 2) , 2) 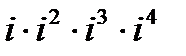 . Решить упражнение № 2. Решите уравнение: х2+81=0. . Решить упражнение № 2. Решите уравнение: х2+81=0. | 0,5 | |
| Раздел 5. Основы математического анализа. | |||
| 21. | Тема 5.1. Предел функции и его свойства. | Решить упражнение № 1. Вычислите пределы: 1) 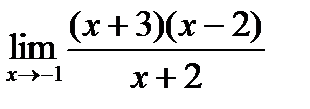 , 2) , 2) 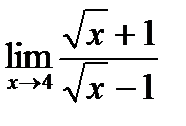 . . | |
| 22. | Тема 5.2. Непрерывность функции. Точки разрыва, их классификация. | Решить упражнение № 1. Вычислите пределы: 1) 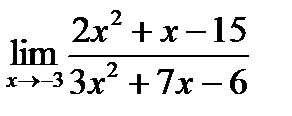 ;2) ;2) 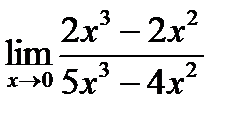 , 3) , 3) 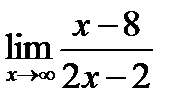 . . | |
| 23. | Тема 5.3. Замечательные пределы, способы раскрытия неопределенностей. | Решить упражнение № 1. Вычислите пределы: 1) 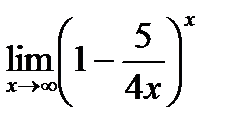 , 2) , 2) 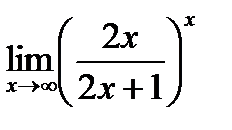 . . | |
| 24. | Решить упражнение № 1. Вычислите пределы: 1) 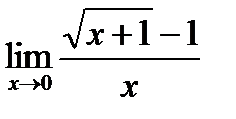 , 2) , 2) 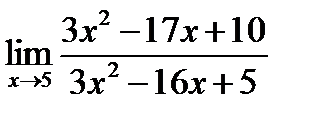 . . | ||
| Раздел 6. Дифференциальное исчисление функции одной действительной переменной. | |||
| 25. | Тема 6.1. Производная. Правила дифференцирования. Физический и геометрический смысл производной. | Решить упражнение № 1. Найдите производные следующих функций: 1)  , 2) , 2) 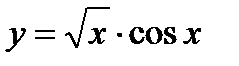 , 3) , 3) 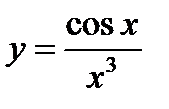 . Решить задачу № 1. . Решить задачу № 1.  | |
| 26. | Тема 6.2. Производная сложной функции. Производные высших порядков. | Решить упражнение № 1. Найдите производные следующих функций: 1) 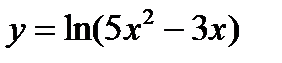 , 2) , 2) 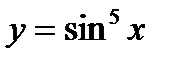 , 3) , 3) 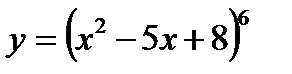 . . | |
| 27. | Решить упражнение № 1. Найдите производные следующих функции: 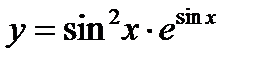 . . | ||
| 28. | Тема 6.3. Дифференциал функции. | Решить упражнение № 1. 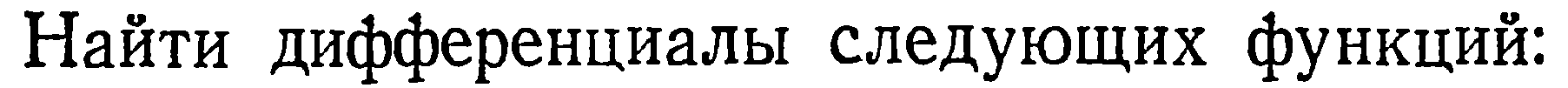 1) 1) 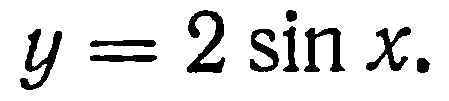 , 2) , 2) 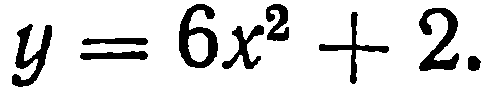 | |
| 29. | Тема 6.4. Исследование функций с помощью производной. | Решить упражнение № 1.  1) 1) 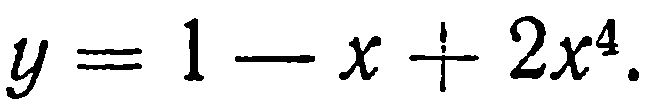 , 2) , 2) 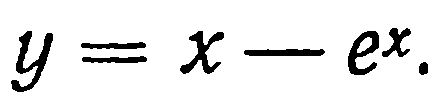 Решить упражнение № 2. Решить упражнение № 2. 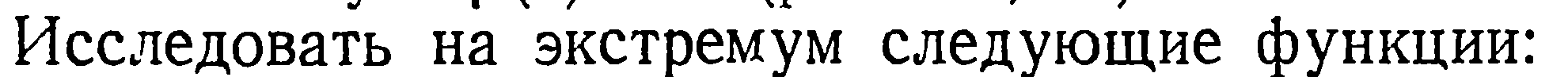 1) 1) 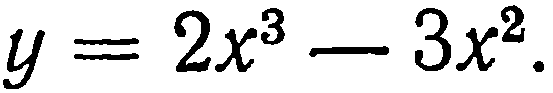 , 2) , 2) 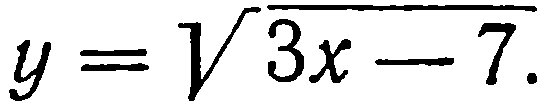 | 0,5 |
| 30. | Решить упражнение № 1. 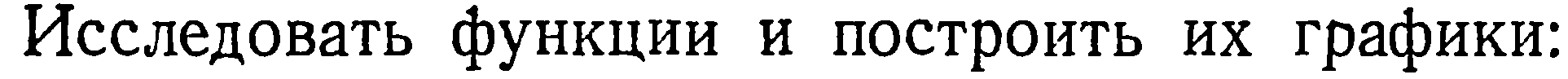 1) 1) 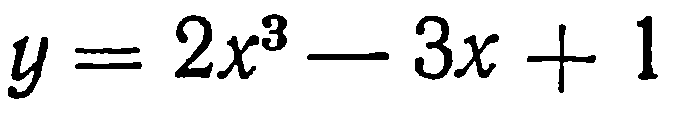 , 2) , 2) 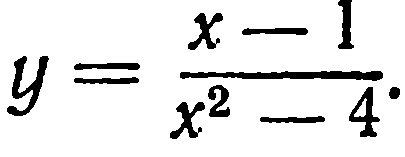 | 0,5 | |
| Раздел 7. Интегральное исчисление функции одной переменной. | |||
| 31. | Тема 7.1. Неопределенный интеграл и его свойства. | Решить упражнение № 1. Найдите интегралы:1) 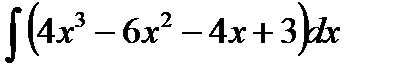 , 2) , 2) 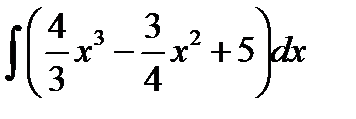 . Решить упражнение № 2. Найдите интегралы:1) . Решить упражнение № 2. Найдите интегралы:1) 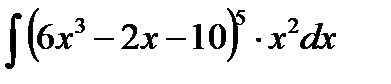 , 2) , 2) 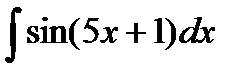 . . | |
| 32. | Решить упражнение № 1. Найти интеграл 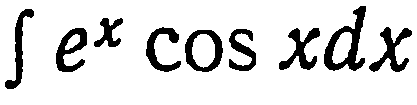 . . | 0,5 | |
| 33. | Решить упражнение № 1. Найти интеграл 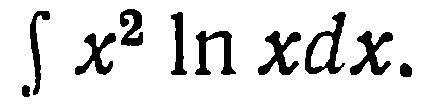 | 0,5 | |
| 34. | Тема 7.2. Определенный интеграл и его свойства. | Решить упражнение № 1. Найдите интегралы:1) 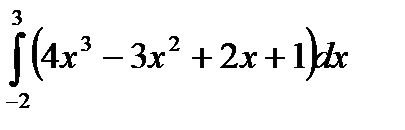 , 2) , 2) 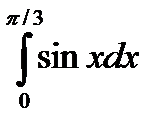 . Решить задачу № 1. . Решить задачу № 1. 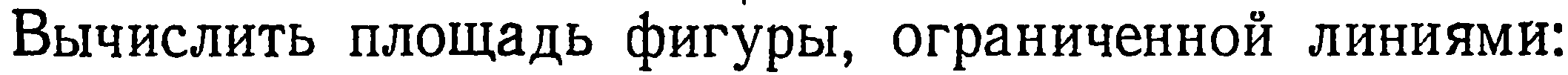 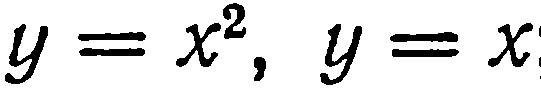 . . | |
| 35. | Решить упражнение № 1.  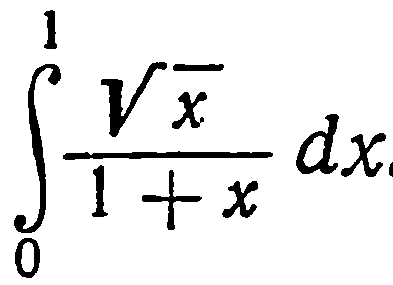 , , 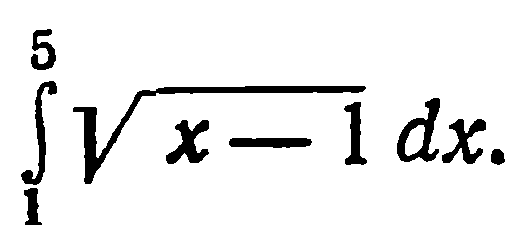 | 0,5 | |
| 36. | Решить упражнение № 1. Применяя формулу интегрирования по частям, вычислить интеграл: 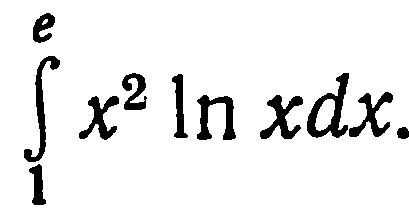 . . | 0,5 | |
| 37. | Тема 7.3. Несобственные интегралы. | Решить упражнение № 1.  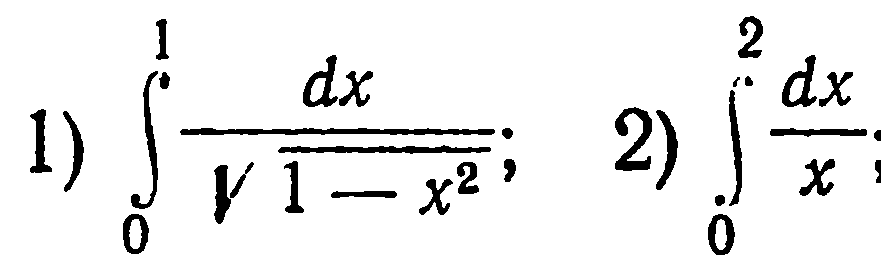 | |
| Раздел 8. Дифференциальное исчисление функции нескольких действительных переменных. | |||
| 38. | Тема 8.1. Дифференцируемость функции нескольких переменных. Понятие частной производной. | Решить упражнение № 1. 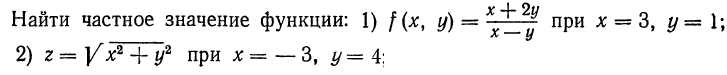 Решить упражнение № 2. Решить упражнение № 2. 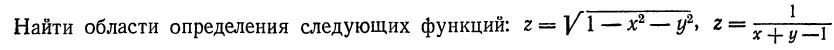 | |
| 39. | Решить упражнение № 1. Найти частные производные следующих функций: 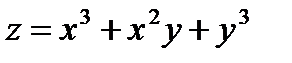 , , 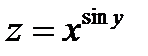 . . | ||
| 40. | Решить упражнение № 1.  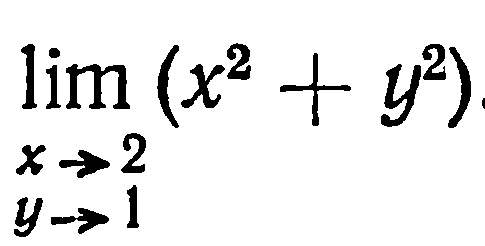 , , 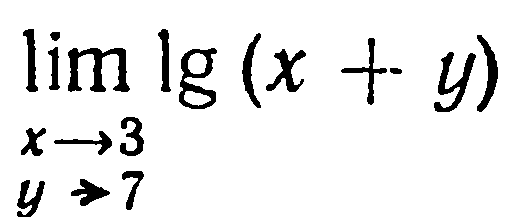 . . | ||
| Раздел 9. Интегральное исчисление функции нескольких действительных переменных. | |||
| 41. | Тема 9.1. Двойные интегралы и их свойства. | Решить упражнение № 1. 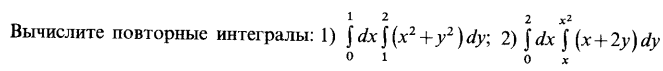 | |
| 42. | Решить упражнение № 1. 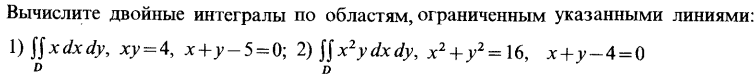 | 0,5 | |
| 43. | Решить упражнение № 1. 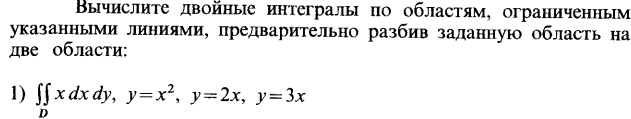 | 0,5 | |
| Раздел 10. Обыкновенные дифференциальные уравнения. | |||
| 44. | Тема 10.1. Обыкновенные дифференциальные уравнения. Общее и частное решения. | Решить упражнение № 1. Найдите общее решение уравнения: 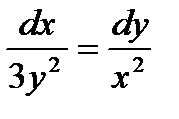 . Решить упражнение № 2. Найдите частное решение уравнения, удовлетворяющее указанным начальным условиям: . Решить упражнение № 2. Найдите частное решение уравнения, удовлетворяющее указанным начальным условиям: 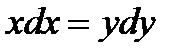 , , 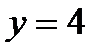 при при 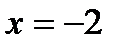 . . | 0,5 |
| 45. | Тема 10.2. Решение дифференциальных уравнений 1-го порядка. | Решить упражнение № 1. Найдите общие решения уравнений: 1) 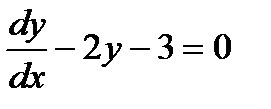 . . | |
| 46. | Решить упражнение № 1. Найдите общие решения уравнений: 1) 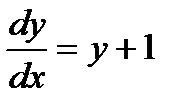 . . | 0,5 | |
| 47. | Решить упражнение № 1. Найдите частные решения уравнений, удовлетворяющие указанным начальным условиям: 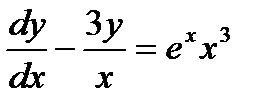 ; ; 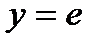 при при 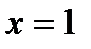 . . | 0,5 | |
| 48. | Решить задачу № 1. Ускорение точки, движущейся прямолинейно, задано уравнением 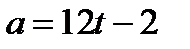 . Найти закон движения этой точки, если в момент времени . Найти закон движения этой точки, если в момент времени 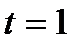 с ее скорость с ее скорость 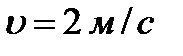 и путь и путь 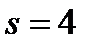 м. м. | 0,5 | |
| 49. | Тема 10.3. Дифференциальные уравнения 2-го порядка. | Решить упражнение № 1. Решите уравнения: 1) 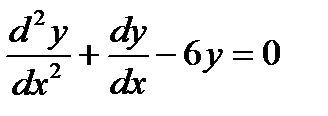 , 2) , 2) 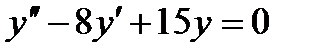 . . | |
| 50. | Решить упражнение № 1. Решите уравнение: 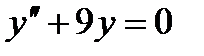 . . | 0,5 | |
| 51. | Решить задачу № 1. Ускорение точки, движущейся прямолинейно, задано уравнением 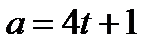 . Найти закон движения этой точки, если в момент времени . Найти закон движения этой точки, если в момент времени 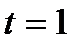 с ее скорость с ее скорость 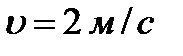 и путь и путь 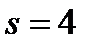 м. м. | 0,5 | |
| Всего: |
2. Общие методические рекомендации различных видов внеаудиторной самостоятельной работы.
Приложение 1
Приложение 2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
"МУРМАНСКИЙ АРКТИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ" (ФГБОУ ВО "МАГУ")
Филиал МАГУ в г. Кировске
| СОГЛАСОВАНО Зам. директора филиала по УиВР _____________ В.А. Ганичева "" 20г. | УТВЕРЖДАЮ Директор филиала __________А.А. Разумовская "" 20г. | |
| СОГЛАСОВАНО Ведущий специалист по УМР _____________ Е.А. Ярославцева "" 20г. |
ЗАДАНИЯ
для внеаудиторной самостоятельной работы студентов
по учебной дисциплине ЕН.01. Элементы высшей математики
для специальности 09.02.03 Программирование в компьютерных системах
Преподаватель: ___________ Орлова О.А.
Рекомендован к утверждению на заседании цикловой комиссии:
Протокол №_____от «____» __________ 201__ г.
Председатель цикловой комиссии _______________ Котович Е.А.
Кировск
2016
СОДЕРЖАНИЕ
Введение. 3
1. Задания для внеаудиторной (домашней) самостоятельной работы по учебной дисциплине ЕН.03. Теория вероятностей и математическая статистика. 5
2. Общие методические рекомендации различных видов внеаудиторной самостоятельной работы. 13
2.1. Методические указания по написанию реферата. 13
2.2. Методические указания по подготовке мультимедийных презентаций. 14
2.3. Методические указания по решению задач и упражнений. 16
2.4. Методические указания по выполнению заданий с привлечением информационных технологий. 17
3. Рекомендуемая литература для выполнения внеаудиторной (домашней) самостоятельной работы. 18
Приложение 1. Темы для выполнения реферата и мультимедийной презентации. 19
Приложение 2. График защиты рефератов и мультимедийных презентаций. 20
Введение.
Требованиями образовательной программы предусмотрено обязательное выполнение обучающимися по каждой учебной дисциплине определенного объема внеаудиторной самостоятельной работы.
В ходе изучения дисциплины ЕН.01. Элементы высшей математики предусмотрена внеаудиторная (домашняя) самостоятельная работав объеме 50 часов.
Наличие положительной оценки каждого задания внеаудиторной самостоятельной работы необходимо для получения зачета по дисциплине и допуска к экзамену, поэтому в случае невыполнения работы по любой причине или получения неудовлетворительной оценки за самостоятельную работу вы должны найти время для ее выполнения и пересдачи.
Домашнее задание выполняется студентами в целях:
- развитие общих и профессиональных компетенций;
- углубление и расширение теоретических знаний;
- формирование умений использовать справочную и специальную литературу;
- развитие познавательных способностей и активности обучающихся;
- формирование самостоятельности мышления, способностей к саморазвитию, совершенствованию и самоорганизации;
- умение использовать материал, собранный и полученный в ходе самостоятельных занятий для эффективной подготовки к экзамену.
Внеаудиторная самостоятельная работа дополняет содержание аудиторных занятий, способствует закреплению, обобщению и систематизации полученных на уроках теоретических знаний и совершенствованию практических умений, а также развитию таких качеств личности, как ответственность и организованность.
Объем времени для выполнения учебного задания определен эмпирически на основании наблюдений за выполнением студентами аудиторной самостоятельной работы; опроса студентов о затратах времени на выполнение того или иного внеаудиторного задания; хронометража собственных затрат на решение той или иной задачи с внесением поправочного коэффициента из расчета уровня знаний и умений студентов по дисциплине.
Домашнее задание по элементам высшей математики состоит из следующих видов работ:
1) написание рефератов;
2) создание мультимедийных презентаций;
3) решение задач и упражнений;
4) выполнение заданий с привлечением информационных технологий.
Формами контроля по написанию рефератов и созданию мультимедийных презентаций является защита реферата и представление презентации. Письменное решение задач и упражнений выполняется в отдельной тетради для самостоятельных работ и сдается преподавателю. Формой контроля является просмотр и проверка выполнения домашнего задания. Задания с привлечением информационных технологий выполняются на компьютере и сдаются преподавателю в электронном виде. Формой контроля по выполнению заданий с привлечением информационных технологий является просмотр и проверка выполнения домашнего задания.
Для каждого вида внеаудиторной самостоятельной работы ниже приведены методические указания по выполнению.
Обратите внимание, что все виды заданий для внеаудиторной самостоятельной работы представлены в таблице, там же указан примерный объем времени на выполнение задания. Таблица будет являться вашим ориентиром в выполнении домашней работы.
Оценка за выполнение домашнего задания выставляется в журнал учебных занятий.
Уважаемый студент!
| Желаем удачи! |
| Ознакомьтесь с таблицей заданий внеаудиторной (домашней) самостоятельной работы и перечнем рекомендуемой литературы |
| Прежде чем приступить к выполнению внеаудиторной самостоятельной работы, прочтите Введение |
| Прочтите методические указания по выполнению некоторых заданий внеаудиторной самостоятельной работы |
| Выполните задание |
| Упражнения и задачи должны быть выполнены к следующему учебному занятию, реферат и презентация выполняется в соответствии с графиком (приложение 2) |
| Если у вас возникнут затруднения в процессе работы, обратитесь к преподавателю |
1. Задания для внеаудиторной (домашней) самостоятельной работы по учебной дисциплине ЕН.03. Теория вероятностей и математическая статистика
Таблица
| № дом. задания | Номер и наименование разделов, тем | Задания для внеаудиторной (домашней) самостоятельной работы | Примерный объем времени на выполнение, в час. |
| 1. | Из предложенной тематики (приложение 1) выбрать одну тему. По этой теме подготовить реферат и создать к нему мультимедийную презентацию. | ||
| Раздел 1. Элементы линейной алгебры. | |||
| 2. | Тема 1.1. Матрицы и действия над ними. | Решить упражнение № 1. 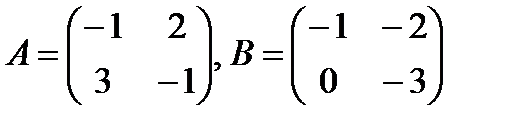 . Найти Ат-3В. Решить упражнение № 2. Найдите произведение матриц: а) . Найти Ат-3В. Решить упражнение № 2. Найдите произведение матриц: а) 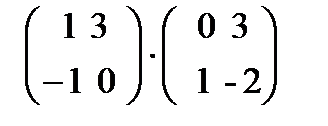 , б) , б) 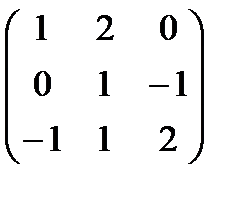 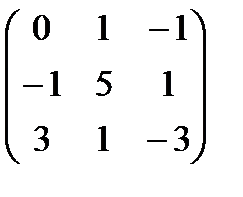 . . | |
| 3. | Тема 1.2. Определитель матрицы и его свойства. | Решить упражнение № 1. Вычислите определители: 1) 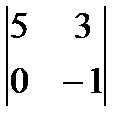 ; 2) ; 2) 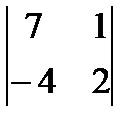 ; 3) ; 3) 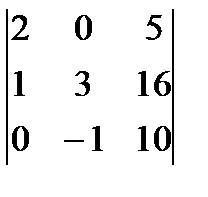 ; 4) ; 4) 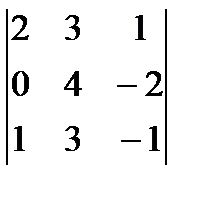 . . | |
| 4. | Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Вычислить определитель второго, третьего, четвертого, пятого и десятого порядка. При введении исходных данных, результат должен вычисляться автоматически. | ||
| 5. | Тема 1.3. Обратная матрица. Ранг матрицы. | Решить упражнение № 1. Найдите матрицу, обратную данной: 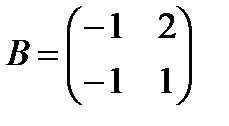 . . | |
| 6. | Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Найдите матрицу, обратную данной: 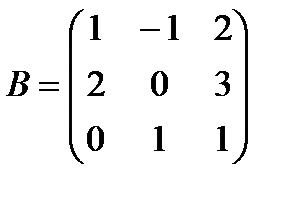 . При введении исходных данных, результат должен вычисляться автоматически. . При введении исходных данных, результат должен вычисляться автоматически. | ||
| Раздел 2.Системы линейных уравнений и методы их решения. | |||
| 7. | Тема 2.1.СЛАУ, общее решение. Частное и базисное решение. | Решить упражнение № 1. Решите системы линейных уравнений: 1) 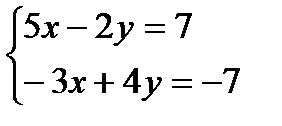 ; 2) ; 2) 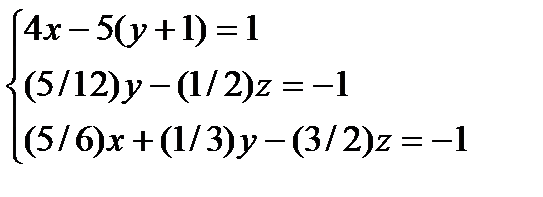 . . | |
| 8. | Тема 2.2. Решение СЛАУ методом Крамера и матричным методом. | Решить упражнение № 1. Решите систему линейных уравнений по правилу Крамера и матричным методом: 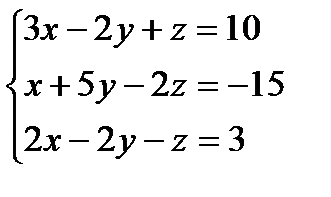 . . | |
| 9. | Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Решите системы линейных уравнений методом обратной матрицы и методом Крамера: 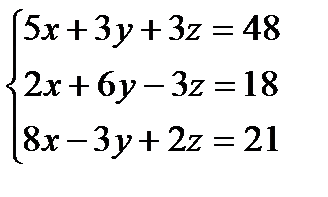 При введении исходных данных, результат должен вычисляться автоматически. При введении исходных данных, результат должен вычисляться автоматически. | ||
| 10. | Тема 2.3. Решение СЛАУ методом Гаусса. | Решить упражнение № 1. Решите систему линейных уравнений методом Гаусса: 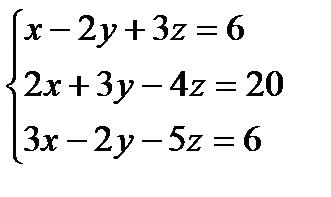 . . | |
| 11. | Решение СЛАУ методом Гаусса. Выполнить задание (с привлечением информационных технологий) № 1. Оформите в MS Excel решение задачи: Решите систему линейных уравнений методом Гаусса: 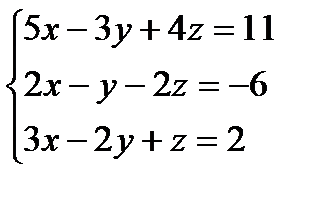 . При введении исходных данных, результат должен вычисляться автоматически. . При введении исходных данных, результат должен вычисляться автоматически. | ||
| Раздел 3. Элементы аналитической геометрии. | |||
| 12. | Тема 3.1. Векторы. Операции над векторами. | Решить задачу № 1.  Решить задачу № 2. Решить задачу № 2. 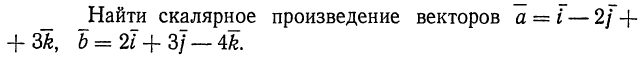 | 0,5 |
| 13. | Решить задачу № 1. 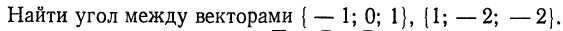 | 0,5 | |
| 14. | Тема 3.2. Уравнение прямой на плоскости. | Решить задачу № 1. 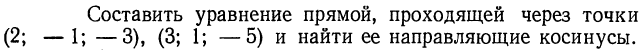 | |
| 15. | Тема 3.3. Кривые второго порядка. | Решить задачу № 1.  Решить задачу № 2. Решить задачу № 2. 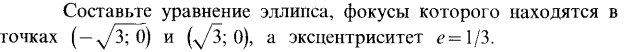 | |
| 16. | Решить задачу № 1. 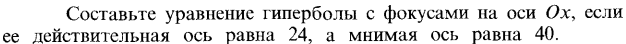 Решить задачу № 2. Решить задачу № 2. 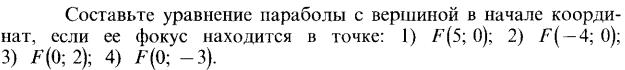 | 0,5 | |
| 17. | Решить задачу № 1.  | 0,5 | |
| Раздел 4. Основы теории комплексных чисел. | |||
| 18. | Тема 4.1. Комплексные числа, действия над ними. | Решить упражнение № 1. Найдите модуль и главное значение аргумента комплексных чисел: 1) -3i; 2) -2-2i; 3) 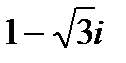 . Решить упражнение № 2. Даны числа z1 и z2. Найдите . Решить упражнение № 2. Даны числа z1 и z2. Найдите 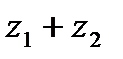 , , 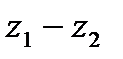 , , 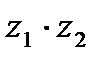 , , 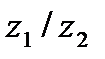 . 1) . 1) 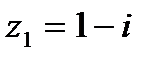 и и 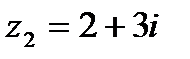 ; 2) . ; 2) . 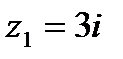 и и 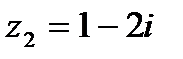 | |
| 19. | Решить упражнение № 1. Представьте в тригонометрической форме комплексные числа: 1) 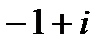 ; 2) ; 2) 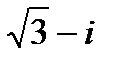 . Решить упражнение № 2. Выполните действия: 1) . Решить упражнение № 2. Выполните действия: 1) 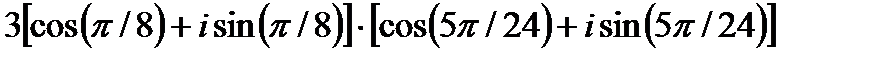 ; 2) ; 2) 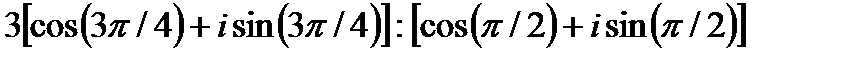 . . | 0,5 | |
| 20. | Решить упражнение № 1. Вычислите: 1) 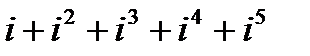 , 2) , 2) 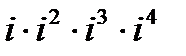 . Решить упражнение № 2. Решите уравнение: х2+81=0. . Решить упражнение № 2. Решите уравнение: х2+81=0. | 0,5 | |
| Раздел 5. Основы математического анализа. | |||
| 21. | Тема 5.1. Предел функции и его свойства. | Решить упражнение № 1. Вычислите пределы: 1) 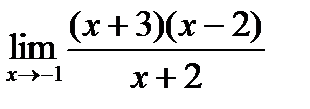 , 2) , 2) 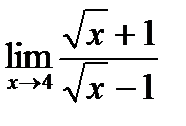 . . | |
| 22. | Тема 5.2. Непрерывность функции. Точки разрыва, их классификация. | Решить упражнение № 1. Вычислите пределы: 1) 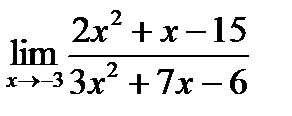 ;2) ;2) 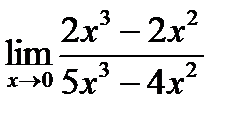 , 3) , 3) 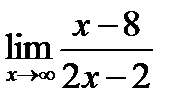 . . | |
| 23. | Тема 5.3. Замечательные пределы, способы раскрытия неопределенностей. | Решить упражнение № 1. Вычислите пределы: 1) 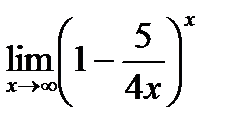 , 2) , 2) 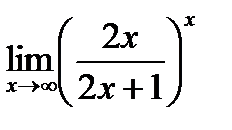 . . | |
| 24. | Решить упражнение № 1. Вычислите пределы: 1) 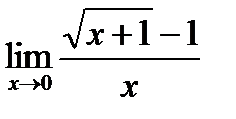 , 2) , 2) 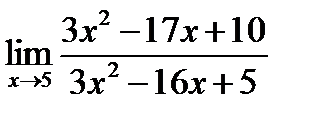 . . | ||
| Раздел 6. Дифференциальное исчисление функции одной действительной переменной. | |||
| 25. | Тема 6.1. Производная. Правила дифференцирования. Физический и геометрический смысл производной. | Решить упражнение № 1. Найдите производные следующих функций: 1)  , 2) , 2) 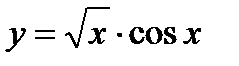 , 3) , 3) 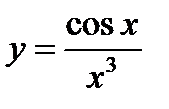 . Решить задачу № 1. . Решить задачу № 1.  | |
| 26. | Тема 6.2. Производная сложной функции. Производные высших порядков. | Решить упражнение № 1. Найдите производные следующих функций: 1) 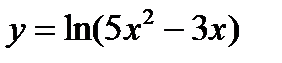 , 2) , 2) 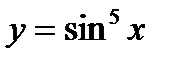 , 3) , 3) 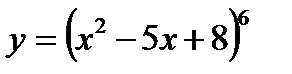 . . | |
| 27. | Решить упражнение № 1. Найдите производные следующих функции: 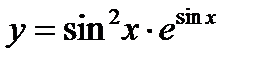 . . | ||
| 28. | Тема 6.3. Дифференциал функции. | Решить упражнение № 1.  1) 1) 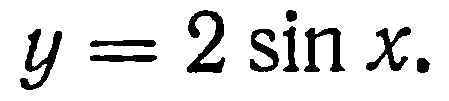 , 2) , 2) 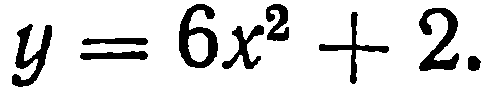 | |
| 29. | Тема 6.4. Исследование функций с помощью производной. | Решить упражнение № 1.  1) 1) 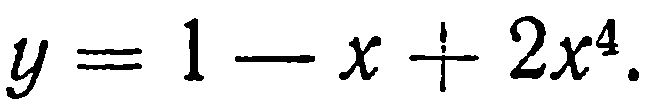 , 2) , 2) 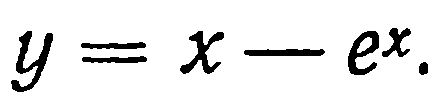 Решить упражнение № 2. Решить упражнение № 2. 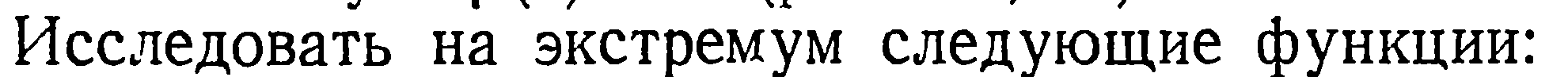 1) 1) 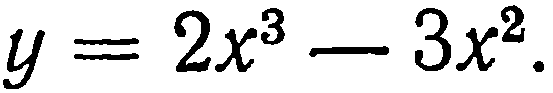 , 2) , 2) 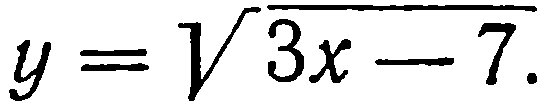 | 0,5 |
| 30. | Решить упражнение № 1.  1) 1) 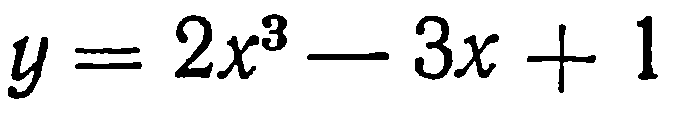 , 2) , 2) 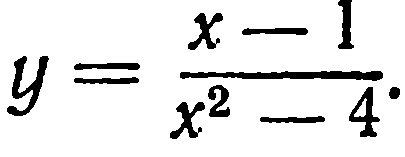 | 0,5 | |
| Раздел 7. Интегральное исчисление функции одной переменной. | |||
| 31. | Тема 7.1. Неопределенный интеграл и его свойства. | Решить упражнение № 1. Найдите интегралы:1) 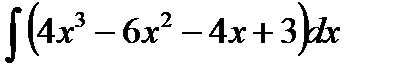 , 2) , 2) 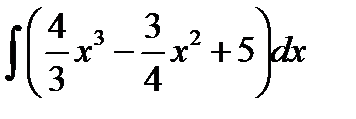 . Решить упражнение № 2. Найдите интегралы:1) . Решить упражнение № 2. Найдите интегралы:1) 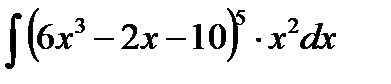 , 2) , 2) 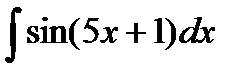 . . | |
| 32. | Решить упражнение № 1. Найти интеграл 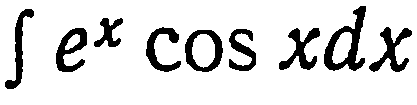 . . | 0,5 | |
| 33. | Решить упражнение № 1. Найти интеграл 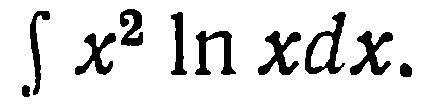 | 0,5 | |
| 34. | Тема 7.2. Определенный интеграл и его свойства. | Решить упражнение № 1. Найдите интегралы:1) 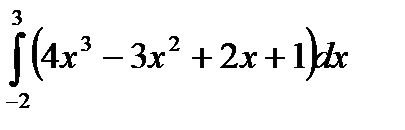 , 2) , 2) 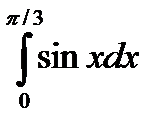 . Решить задачу № 1. . Решить задачу № 1.  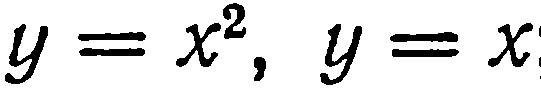 . < . < Наши рекомендации
|
