Использование ППП Eureka и Excel при решении задач оптимизации
Использование ППП Eureka для поиска экстремумов функций одной переменной.
Для поиска максимумов функций одной переменной необходимо в окне Edit набрать
$|__|max(F)
y(x)=
F=y(x)
В окне Solution будет выдано решение
F=
x=
Перед решением задачи весьма полезно оценить вид функции, экстремум которой необходимо найти и уточнить интервал x, в котором этот экстремум находится. Для этого достаточно воспользоваться командой Plot в позиции Graf основного меню. Из вида графика сделать вывод о правильности решения.
Использование ППП Excel для поиска экстремумов функций одной переменной.
Для поиска максимумов функций одной переменной необходимо:
Вызвать Подбор параметра, с помощью команды в меню Сервис.Окно Подбор параметра состоит из трех полей:
- Установить целевую ячейку, в котором ставится ссылка на ячейку с формулой (Y);
- Равной – выбираем максимальному значению;
- Изменяя ячейки, в которой ставится ссылка на ячейку с изменяемым параметром (первая граница, а интервала (а,в)).
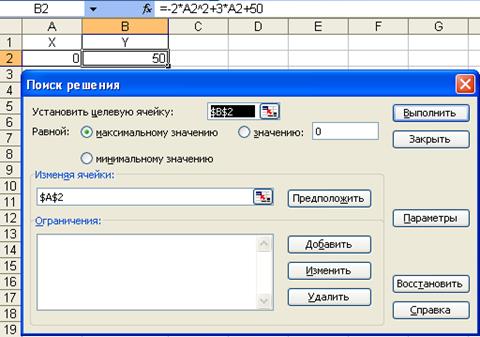
После нажатия кнопки OK, появляется окно, Результаты поиска решения, сохраняем найденное решение. Полученное решение:
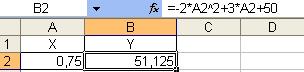
Содержание отчета
1. Содержательная постановка задачи.
2. Исходные данные.
3. Краткое описание методов.
4. Блок схема подпрограмм и блок схема головного (или управляющего) модуля.
5. Листинг подпрограмм и управляющего модуля.
6. Распечатка полученных результатов.
7. Распечатка результатов в Excel и Эврика.
Пример выполнения лабораторной работы
Дана функция y = -2x2 + 3x + 50.
Найти оптимальное значение функции y двумя способами: методом «золотого сечения» и методом «половинного деления». Заданный интервал измерения x (0;1), точность вычисления E = 0.001.
БЛОК-СХЕМА
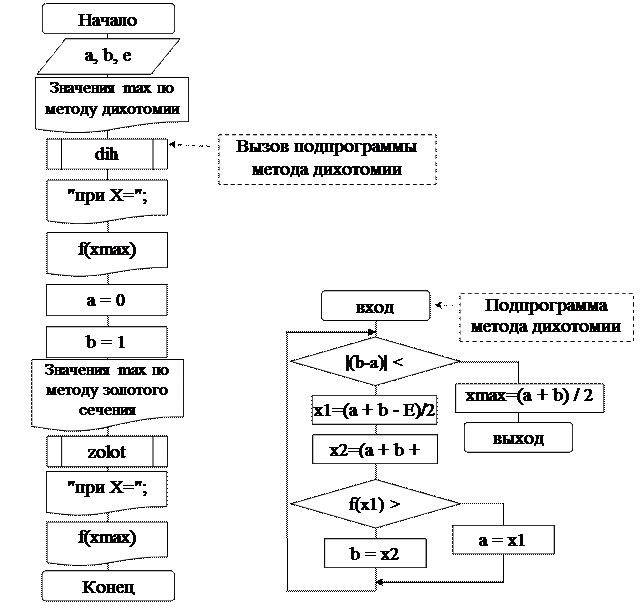
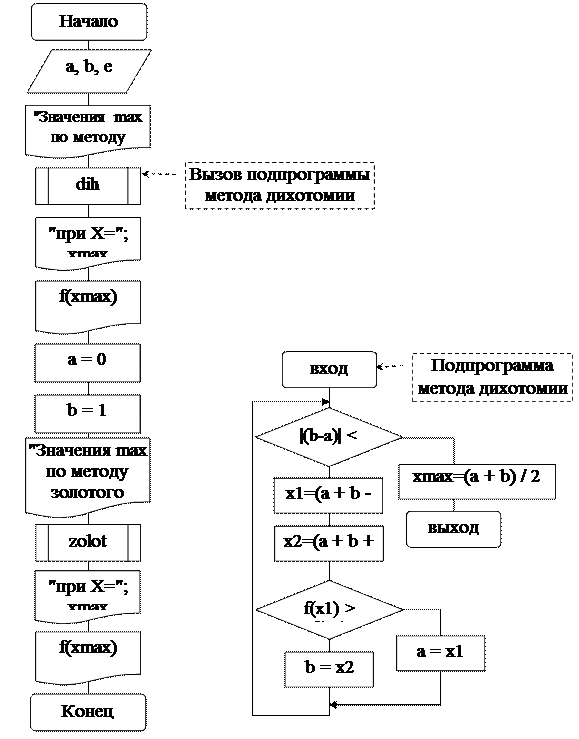
| |
где а, b - нижняя и верхняя границы изменения х;
е - точность вычислений;
dih - процедура вычисления методом половинного деления;
zolot - процедура вычисления методом золотого сечения.
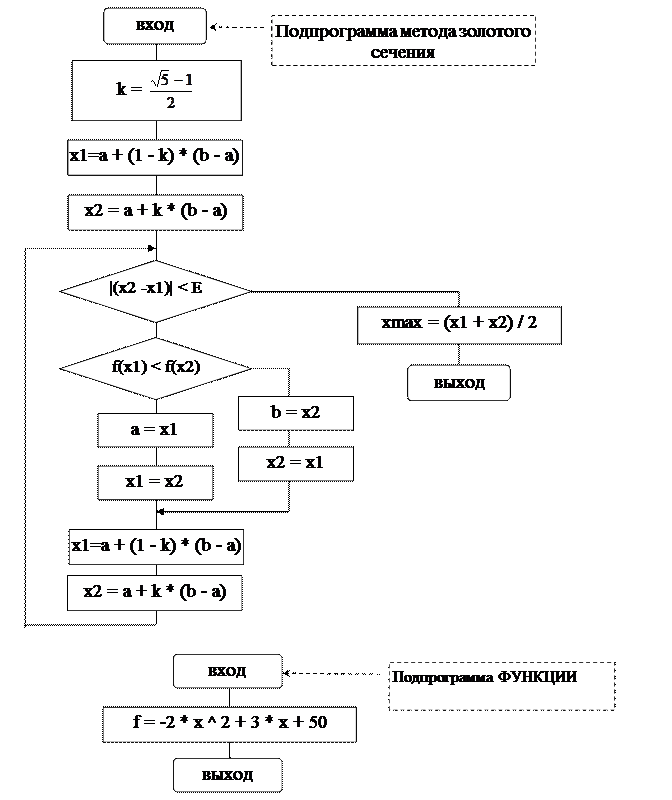
Рис. 9. Блок схема процедуры решения по методу золотого сечения, функция.
ПРОГРАММА НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ QBASIC
DECLARE SUB zolot (a!, b!, E!, xmax!)
DECLARE SUB dih (a!, b!, E!, xmax!)
DECLARE FUNCTION f! (x!)
CLS
INPUT "введите значения отрезка a="; a
INPUT "введите значения отрезка b="; b
INPUT "введите погрешность вычисления Eps="; E
REM метод дихотомии или половинного деления
CALL dih(a, b, E, xmax)
PRINT "Значения max по методу дихотомии"
PRINT "при X="; xmax
PRINT "значение функции Y(xmax)="; f(xmax)
a = 0
b = 1
PRINT "Значение max по методу золотого сечения"
CALL zolot(a, b, E, xmax)
PRINT "при X="; xmax
PRINT "значение функции Y(xmax)="; f(xmax)
END
SUB dih (a, b, E, xmax)
DO UNTIL ABS(b - a) < 2 * E
x1 = (a + b - E) / 2
x2 = (a + b + E) / 2
IF f(x1) > f(x2) THEN
b = x2
ELSE
a = x1
END IF
LOOP
xmax = (a + b) / 2
END SUB
FUNCTION f (x)
f = -2 * x ^ 2 + 3 * x + 50
END FUNCTION
SUB zolot (a, b, E, xmax)
k = (SQR(5) - 1) / 2
x1 = a + (1 - k) * (b - a)
x2 = a + k * (b - a)
DO UNTIL ABS(x2 - x1) < E
IF f(x1) < f(x2) THEN
a = x1
x1 = x2
ELSE
b = x2
x2 = x1
END IF
x1 = a + (1 - k) * (b - a)
x2 = a + k * (b - a)
LOOP
xmax = (x1 + x2) / 2
END SUB
РЕЗУЛЬТАТ в Qbasic
Значение max по методу дихотомии
при X= .7563525
значение функции Y(xmax)= 51.12492
Значение max по методу золотого сечения
при X= .748997
значение функции Y(xmax)= 51.125
