Основные теоретические сведения.

Пусть на отрезке [а,b] задана функция f(x). Определенный интеграл определяется как площадь, ограниченная подынтегральной функцией f(x), осью x и ординатами в точках «a» и «b»

Определенным интегралом от функции f(x) на отрезке [а, b] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения.

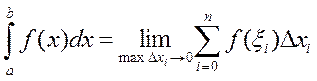
Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно по формуле Ньютона-Лейбница. Она состоит в том, что определенный интеграл равен приращению первообразной F(х) на отрезке интегрирования. На практике этой формулой часто нельзя воспользоваться по двум основным причинам:

Вид функции не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях

Значения функций f(х) заданы таблично (множество х_i конечно)

В этих случаях используются методы численного интегрирования.

Частным случаем в методах численного интегрирования является тот, когда величина элементарного отрезка ∆х,- величина постоянная и может быть вынесена за знак интегральной суммы. Эта величина называется шагом интегрирования и обозначается обычно ∆х.

Рассмотрим методы численного интегрирования.

Метод прямоугольников

В Методе прямоугольников непосредственно используется замена определенного интеграла интегральной суммой. В качестве точек x_i; могут выбираться левые (x_i-1) или правые (x_i) границы элементарных отрезков. Расчетные формулы можно записать так:

При выборе левых границ (см. рис.1)

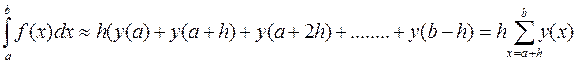
При выборе правых границ (см. рис.2)

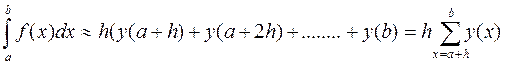
При выборе границ от a+ h/2 до b-h/2

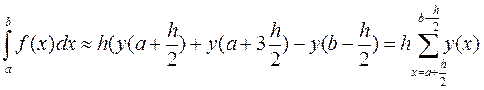
Рис.4

Метод трапеций

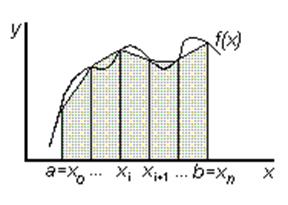В методе трапеций график функции f(х)аппроксимируется ломаной, соединяющей точки с координатами
(x_i, у)

Рис.5

Искомое значение определенного интеграла представляется в виде суммы площадей трапеций, построенных на каждом из элементарных отрезков:

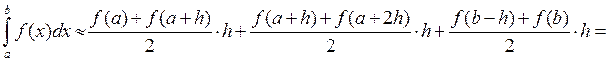
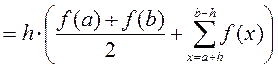
Метод парабол

В методе парабол (формула Симпсона) на каждом из элементарных отрезков по трем известным значениям функции f(Xj) строится парабола, заданная уравнением aх²+bх+с.

Формула для нахождения определенного интеграла может быть выведена из условия равенства значений: у_i = aх_i²+ bx_i +с:

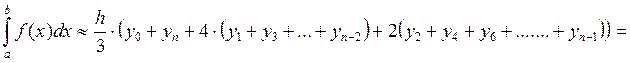
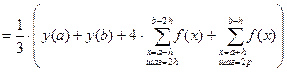
3. Порядок выполнения работы

3.1. Получить у преподавателя вариант задания, включающий в себя подынтегральную функцию (F(Х)), отрезок интегрирования (a,b), точность вычисления значения интеграла (eps).

3.2. Исследовать подынтегральную функцию на непрерывность и существование на заданном отрезке.

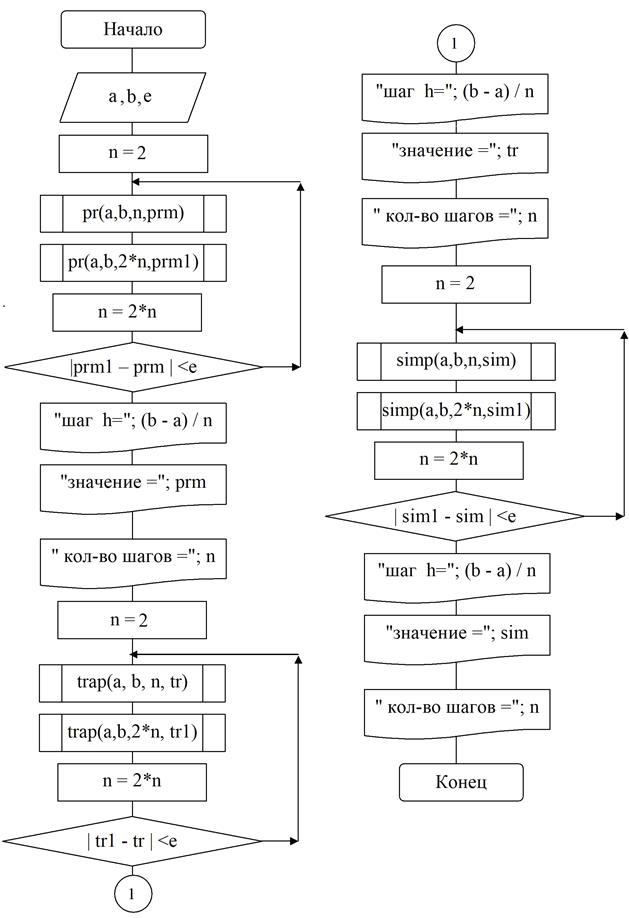
3.3. Составить блок-схему для каждого метода и блок-схему головного модуля.

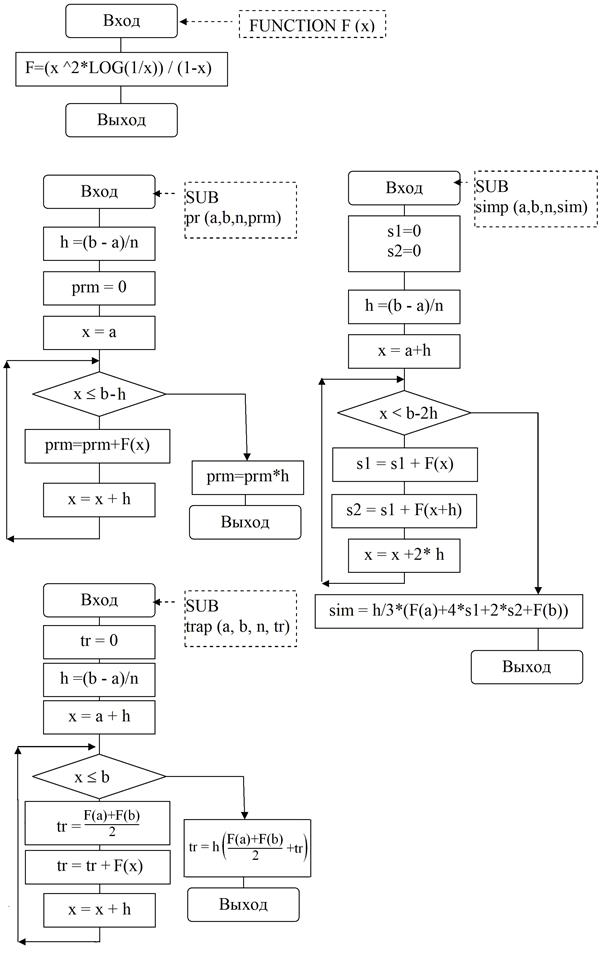
3.4. Написать подпрограмму для каждого метода (прямоугольников, трапеции, парабол).

3.5. Написать головной модуль.

3.6. Отладить программу и получить результаты .

3.7. Проанализировать полученные результаты и сделать выводы.

4. Содержание отчета.

4.1. Математическая постановка задачи.

4.2. Исходные данные.

4.3. Краткое описание методов. Блок-схема для каждого метода. Листинг подпрограмм.

4.4. Блок-схема головного (или управляющего) модуля. Листинг.

4.5. Распечатка полученных результатов.

4.6. Сравнительный анализ полученных результатов разными методами.

Пример выполнения работы

Вычислить интеграл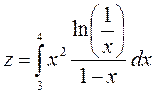

БЛОК-СХЕМА