Переходные процессы в цепи, содержащей R-, L-, и С-элементы
Рассмотрим последовательную цепь, то есть простейшую цепь, содержащую резистивный индуктивный и емкостный элементы (рис. 11.10).

Рассмотрим общий случай входного напряжения u = u(t).
Составим уравнение состояния для этой цепи. Согласно второму закону Кирхгофа имеем:
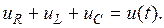
В данной схеме две независимые переменные – ток индуктивности, который является общим для всей цепи, и напряжение на емкости, поэтому для определения переходных напряжений и тока дифференциальное уравнение можно составлять для любой из этих переменных.
Поскольку через все элементы протекает один и тот же ток, удобнее все напряжения выразить через ток
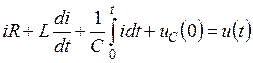 . (11.2)
. (11.2)
В это уравнение ток входит в алгебраической, дифференциальной и интегральной формах. Чтобы свести ток к одной форме, продифференцируем уравнение то времени:
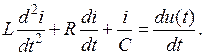 (11.3)
(11.3)
Получили дифференциальное уравнение второго порядка для тока в цепи.
Следует отметить, что порядок уравнения определяется количеством накопителей энергии в цепи. В данном случае имеется два накопителя энергии – индуктивность и емкость, следовательно, получаем дифференциальное уравнение второго порядка.
Решение этого уравнения ищем в виде суммы свободной и принужденной составляющих.
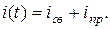
Принужденная составляющая определяется в установившемся режиме при t = ∞ и либо равна нулю 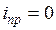 при постоянном напряжении, либо определяется по закону Ома
при постоянном напряжении, либо определяется по закону Ома 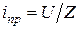 при переменном напряжении.
при переменном напряжении.
Для определения свободной составляющей составляем характеристическое уравнение. Рассмотрим два способа.
1. В уравнении (11.3) приравниваем нулю источники и заменяем символ дифференцирования 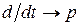 , получим
, получим
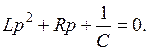
Запишем это уравнение в приведенном виде:
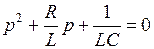 .
.
2. Запишем уравнение для комплексного сопротивления цепи и приравняем его нулю
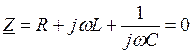 .
.
Сделаем замену 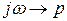 , получим
, получим
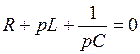 .
.
Приведем это выражение к общему знаменателю
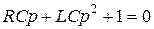 .
.
Запишем приведенное уравнение
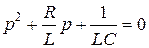 .
.
Получили такое же уравнение, как и в первом случае.
Найдем корни характеристического уравнения
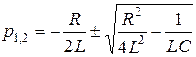 .
.
Проанализируем это выражение. При расчете корней характеристического уравнения возможны три случая.
1. Корни действительные, различные
Если дискриминант больше нуля, а это возможно в том случае, если
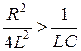 или
или 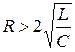 ,
,
то корни будут действительными и различными по величине р1 ≠ р2. В этом случае решение дифференциального уравнения для свободной составляющей ищем в виде
 .
.
Переходной процесс при этом будет апериодическим. График переходного процесса показан кривой 1 на рис. 11.11.
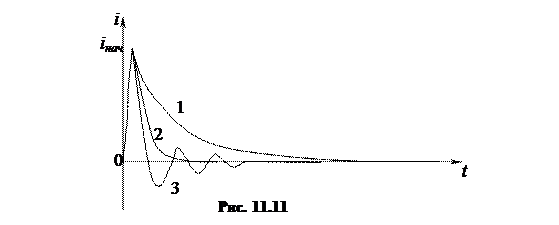 |
2. Корни действительные, равные
Действительные и равные по величине корни р1 = р2 = р будут в том случае, если дискриминант равен нулю, то есть, если
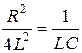 или
или 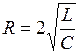 .
.
В этом случае решение для свободной составляющей тока ищем в виде
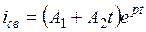 .
.
Переходной процесс также будет апериодическим, но это предельный или критический режим (кривая 2 на рис. 11.11).
3. Корни комплексно-сопряженные
Такой режим будет в том случае, если дискриминант отрицательный, то есть
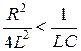 или
или 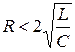 .
.
Корни характеристического уравнения
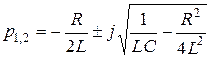 .
.
В этом случае переходной процесс будет затухающим колебательным, то есть ток будет изменяться относительно принужденной составляющей по синусоидальному закону с затухающей амплитудой (кривая 3 на рис. 3.11). Решение для свободной составляющей ищем в виде
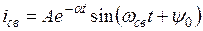 .
.
В этом выражении ввели следующие обозначения:
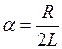 – коэффициент затухания;
– коэффициент затухания;
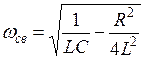 – частота свободных колебаний.
– частота свободных колебаний.
Скорость затухания тока характеризуется декрементом колебаний, равным отношению двух последующих амплитуд
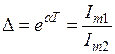 ,
,
где Т = 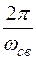 – период затухающих колебаний.
– период затухающих колебаний.
Чаще пользуются логарифмическим декрементом колебаний
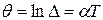 .
.
При любом характере корней свободная составляющая содержит две постоянных интегрирования, то есть две неизвестных величины, для определения которых необходимо составить два уравнения.
Для определения постоянных интегрирования необходимо знать значение тока и всех его производных в начальный момент времени.
Выражения для полного тока и его производной имеют вид:
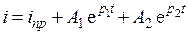 ;
;
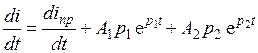 .
.
Запишем исходное уравнение (11.2) при t = 0
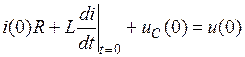 .
.
Напряжение источника и(0), как правило, известно; i(0) и иС(0) – независимые начальные условия, определяемые по состоянию цепи до коммутации и законам коммутации.
Из этого выражения можно найти
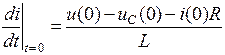 .
.
При t = 0 имеем: 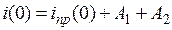
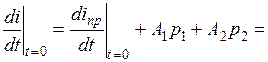
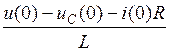 .
.
Решая эти уравнения относительно А1 и А2, находим постоянные интегрирования.
Рассмотрим частные случаи переходных процессов в R-, L-, C-цепи.
