Условия равновесия системы сходящихся сил в геометрической и аналитической формах. Теорема о трех непараллельных силах.
Геометрическое условие равновесия:
Силовой многоугольник должен быть замкнут, т.е. конец последнего вектора должен совпадать с началом первого.
Аналитическое условие равновесия:
Равенство 0 проекций равнодействующей на оси координат (Rx=0, Ry=0, Rz=0).
Для равновесия тел, находящихся под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая была равна 0 (R=0).
Для равновесия тела, находящегося в системе сходящихся сил, необходимо и достаточно, чтобы были равны 0 алгебраические суммы проекций всех сил на оси произвольно выбранных систем координат.
Теорема о трех непараллельных силах:
Используется когда известны величина и направление одной силы, линия действия другой и точка приложения третьей.
Линии действия трех непараллельных уравновешенных сил, лежащих в одной плоскости, пересекаются в одной точке.
R12=F1+F2
Равновесие равнодействующей R12 сил F1 и F2 возможно только в том случае, если третья сила F3 будет направлена по линии действия R12 противоположно ей, т.е. проходить через точку пересечения линии действия сил F1 и F2.
Сложение параллельных сил.
Равнодействующая двух параллельных сил, направленных в одну сторону равна алгебраической сумме модулей составляющих сил. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Две параллельные, противоположно направленные силы, не равные по модулю, эквиваленты равнодействующей, модуль которой равен разности модулей слагаемых сил и направлены в сторону большей силы. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Если модули противоположно направленных сил равны, то такая система не имеет равнодействующей, она сообщает свободному телу вращательное движение и называется парой сил.
Векторный момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения. Аналитическое выражение момента силы относительно точки.
Алгебраическим моментом силы F относительно некоторого центра называется взятое со знаком + или - произведение модуля силы F на плечо (кротчайшее расстояние от точки до линии действия силы). Момент положителен, если сила стремиться вращать плоскость действия против часовой стрелки и наоборот. (M=F*h) Но при этом h можно выразить через радиус-вектор r (h=r*sin α), тогда M = F*r*sin α = (F x r). Получаем, что векторный момент силы относительно точки – векторная величина.
Момент силы относительно оси. Аналитическое выражение момента силы относительно оси.
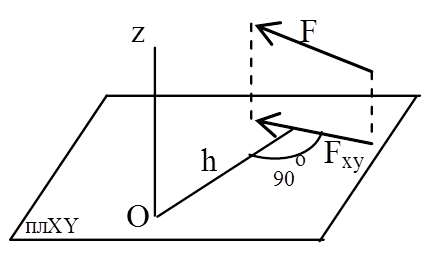 Момент силы относительно оси – скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Момент силы относительно оси – скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
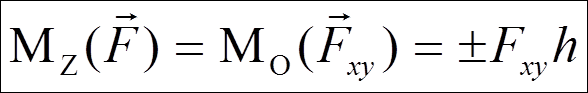
Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси.
Момент силы относительно оси равен 0 в двух случаях:
ü Если сила параллельна оси
ü Если сила пересекает ось
Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0.
