Перевод из 10-ой системы в 8-ую

Перевод целой части

Алгоритм перевода из десятичной системы в систему счисления с ос­но­ва­нием q путем деления и записи остатков в обратном порядке более удо­бен, поэтому для перевода числа в 8-ю и 16-ую системы мы будем использовать его.

Рассмотрим перевод числа 567 в систему счисления с основанием 8.

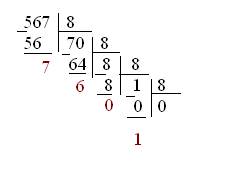
567 = 1067₈

Перевод дробной части

Переведем 0.65625 в 8-ю систему счисления.

Умножаем дробную часть на 8:

целая часть дробная часть

произведения произведения

5 25 Умножаем только дробную часть!

2 0

0.65625 = 0.52₈

Перевод из 10-ой системы в 16-ую

Перевод целой части

Делим число на 16 и записываем остатки в обратном порядке:

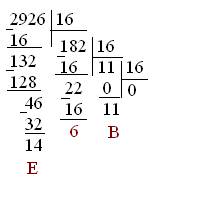
В шестнадцате­рич­ной системе счисления необходимо заменить 10 на A, 11 на B и так да­лее.

Перевод дробной части

Переведем 0.65625 в 16-ю систему счисления.

Умножаем дробную часть на 16:

целая часть дробная часть

произведения произведения

10(A) 5 Умножаем только дробную часть!

8 0

0.65625 = 0.A8₁₆

Перевод из 2-ой системы в 8-ю или 16-ю и обратно

Пожалуй, проще всего осуществляется перевод чисел из двоичной сис­темы в системы с основанием, равным степеням двойки (8 или 16), и наобо­рот. Для того чтобы целое двоичное число записать в системе счисления с ос­нованием 2ⁿ, нужно

· данное двоичное число разбить на группы по n-цифр в каждой справа налево в целой части и слева-направо в дробной;

· если в последней группе окажется меньше n разрядов, то до­пол­нить ее нулями до нужного числа разрядов;

· рассмотреть каждую группу, как n-разрядное двоичное число, и заме­нить ее соответствующей цифрой в системе счисления с основанием 2ⁿ.

Таблица перевода из двоичной системы в 16-ю и обратно

Десятичное значение	Двоичный код	Шестнадцате-ричная цифра
		A
		B
		C
		D
		E
		F

Часть таблицы, выделенная бирюзовым, может использоваться для перевода из 2-й системы в 8-ю и обратно.

Примеры:

1) Переведем число 11101.00111₂ из двоичной системы в восьмеричную.

Разбиваем двоичное число на тройки цифр:

11101.00111₂ = 011 101.001 110₂ = 35.16₈

Заменяем каждую тройку двоичных цифр соответствующей 8-й цифрой (см. таблицу).

Для перевода числа из 8-й системы счисления в 2-ю нужно каждую 8-ю цифру заменить тройкой двоичных цифр (рассмотрите тот же пример справа-налево).

2) Переведем число 10000.110111₂ в 16-ю систему.

Разбиваем двоичное число на четверки цифр:

10000.110111₂ = 0001 0000.1101 1100₂ = 10.DC₁₆

Заменяем каждую четверку двоичных цифр соответствующей 16-й циф­рой (см. таблицу).

Для перевода числа из 16-й системы счисления в 2-ю нужно каждую 16-ю цифру заменить четверкой двоичных цифр (рассмотрите тот же пример спра­­ва-налево).

Примеры двоичного кодирования информации

Среди всего разнообразия информации, обрабатываемой на компьютере, значительную часть составляют числовая, текстовая, графическая и аудио­ин­формация. Познакомимся с некоторыми способами кодирования этих типов информации в ЭВМ.

Кодирование чисел

Существуют два основных формата представления чисел в памяти ком­пьютера. Один из них используется для кодирования целых чисел, второй (так называемое представление числа в формате с плавающей точкой) используется для задания некоторого подмножества действительных чисел.

Кодирование целых чисел

Множество целых чисел, представимых в памяти ЭВМ, ограничено. Ди­а­пазон значений зависит от размера области памяти, используемой для раз­ме­ще­ния чисел. В k-разрядной ячейке может храниться 2^k различных значе­ний целых чисел.

Целые числа могут занимать 1, 2, 4 или 8 байт (для 64-разрядных ма­шин).

Чтобы получить внутреннее представление целого положительного чис­ла N, хранящегося в k-разрядном машинном слове, необходимо:

1. перевести число N в двоичную систему счисления;

2. полученный результат дополнить слева незначащими нулями до k разрядов.

Код целого числа может рассматриваться как двоичное число со знаком или без знака.

При беззнаковом представлении все разряды используются для за­писи значения числа.

Пример:

Число 107 = 1101011₂ будет записано:

в 1 байт как 01101011

в 2 байта как 00000000 01101011

1-й байт 0-й байт

в 4 байта как 00000000 00000000 00000000 01101011

3-й байт 2-й байт 1-й байт 0-й байт

Минимальное беззнаковое число равно 0. Максимальное беззнаковое число равно 2ⁿ – 1, где n – кол-во двоичных разрядов, используемых для за­писи числа.

Например для 2-хбайтового представления max =11111111 11111111₂ =
1 00000000 00000000 – 1 = 2¹⁶ – 1 = 65 535

Для записи чисел со знаком старший (левый) разряд отводится под знак числа. Если число неотрицательное, то в знаковый разряд записывается 0, в противном случае – 1, т.е. единица в знаковом разряде означает знак “ми­нус”.

Целые числа со знаком могут быть записаны в прямом, обратном и до­пол­­нительном коде.

В прямом коде число хранится в виде: знак+абсолютное значение (мо­дуль) числа.

В обратном коде в значении числа нули заменяют на единицы, а едини­цы на нули.

Дополнительный код получают путем прибавления 1 к обратному.

Обратный и дополнительный код неотрицательных чисел совпадает с прямым.

Обратный и дополнительный коды чисел позволяют заменить операцию вычитания сложением с отрицательным числом, что существенно упрощает устройство процессора. Варианты арифметических операций будут рас­смот­рены ниже.

Пример. Рассмотрим внутреннее представление целого отрицательного числа: -6 = 110₂.

Однобайтовое:

Прямой код: 1000 0110

Обратный код: 1111 1001

Дополнительный: 1111 1001

⁺ 1

1111 1010

Четырехбайтовое:

Прямой код: 10000000 00000000 00000000 00000110

Обратный код: 1111111 1111111 11111111 11111001

Дополнительный: 1111111 1111111 11111111 11111001

⁺ 1

1111111 1111111 11111111 11111010

Для того, чтобы получить значение отрицательного числа, записанного в дополнительном коде, можно использовать один из двух алгоритмов:

1) вычесть 1 из дополнительного кода (получаем обратный код) и заме­нить все нули на единицы, а единицы на нули;

2) сначала заменить все нули на единицы, единицы на нули, затем при­ба­вить единицу к результату.

Пример: возьмем однобайтовый доп. код : 1111 1010 и используем второй алгоритм: 1111 1010 -- > - (0000 0101 + 1) = - 110₂ = -6.