Перевод из 10-ой системы в 2-ую

Перевод из 10-ой системы целой и дробной частей выполняется по раз­личным алгоритмам, поэтому будем рассматривать их отдельно.

Перевод целой части

Пусть требуется перевести число 567 из десятичной в двоичную сис­те­му. Сначала определим максимальную степень двойки, такую, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, т. к. 2⁹=512, а 2¹⁰=1024, что больше начального числа. Таким образом, мы получим число разрядов результата. Оно равно 9+1=10. Поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные циф­­ры. Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 567-2⁹=55. Остаток сравним с числом 2⁸=256. Так как 55 меньше 256, то девятый разряд будет нулем, т. е. результат примет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 2⁷=128>55, то и он бу­дет нулевым.

Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 2⁵=32<55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55-32=23 справедливо неравенство 2⁴ = 16 < 23, что означает равенство единице пятого разряда. Действуя аналогич­но, получаем в результате число 1000110111. Мы разложили данное число по степеням двойки:

567=1*2⁹ + 0*2⁸ + 0*2⁷ + 0*2⁶ + 1*2⁵ + 1*2⁴ + 0*2³ + 1*2² + 1*2¹ + 1*2⁰

При другом способe перевода чисел используется операция деления в столбик. Рассмотрим то же самое число 567. Разделив его на 2, получим част­ное 283 и остаток 1. Проведем ту же самую операцию с числом 283. Получим частное 141, остаток 1. Опять делим полученное частное на 2, и так до тех пор, пока частное не станет меньше делителя. Теперь для того, чтобы полу­чить число в двоичной системе счисления, достаточно записать последнее частное, то есть 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.

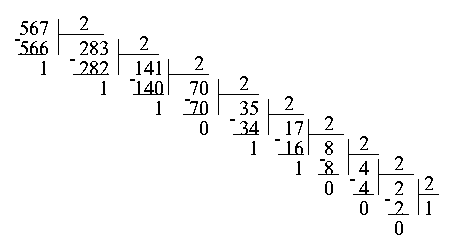
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1000110111.

Поскольку делить на 2 несложно, этот процесс можно записать более компактно:

Частное | Остаток

567 | 1 567 = 1000110111₂

283 | 1

141 | 1

70 | 0

35 | 1

17 | 1

8 | 0

4 | 0

2 | 0

1 | 1

Перевод дробной части

Алгоритм перевода дробной части:

1) последовательно умножать дробную часть на основание новой системы счис­ления, пока не получим нулевую дроб­ную часть или не будет дос­тигнута требуемая точность вычислений.

2) Записать полученные целые части произведений в прямой после­до­ва­тельности

Примеры:

1) перевести 0.65625 в 2-ю систему счисления.

Умножаем дробную часть на 2:

целая часть дробная часть

произведения произведения

1 3125

0 625 Умножаем только дробную часть!

1 25

0 5

1 0

0.65625 = 0.10101₂

2) перевести 0.1 в 2-ю систему счисления.

Умножаем дробную часть на 2:

целая часть дробная часть

произведения произведения

0 2 Умножаем только дробную часть!

0 4 С этого места процесс повторяется

0 8

1 6

1 2

0 4

0 8

1 6

1 2

. . .

0.1 = 0. 0 0011 0011 0011 …

В результате перевода большинства десятичных чисел, имеющих дроб­ную часть, получается число с бес­конечной дробью, поэтому действительные (вещест­венные) числа в ком­пью­тере хранятся не точно!