Построить алгоритм расчета для одного работника.

Желаю хорошей работы!

Лабораторная работа №2

Тема:Виды и формы статистического наблюдения

Цель: получить навыки работы по сбору и оформлению информации.

Задание:

1. Построить алгоритм расчета для полного списка работников.

2. Провести наблюдение. Заполнить таблицу.

3. Выполнить сортировку информации (по алфавиту сотрудников).

4. Построить сравнительную диаграмму окладов и итоговой суммы работников.

5. Составить пояснительную записку о выполненном расчете, приложить ведомость начисления.

Теоретический материал:

Для выполнения работы рекомендуется использовать электронные таблицы Microsoft EXCEL, Microsoft Word для OFFICE 97,98,2000 и созданную в предыдущей работе таблицу.

Расчет заработной платы является частью бухгалтерского учета предприятия, следовательно, – сплошным периодическим наблюдением. Начисление заработной платы происходит в определенный период месяца по штатному расписанию, приказу на начисление, данным отдела кадров, то есть имеет организованную форму. Устанавливаются критические сроки подачи сведений для расчета. Условия начисления заработной платы оговариваются в Уставе предприятия, бизнес-план которого вы разработали.

Размножение (копирование) формул.

1. Выбрать курсором ячейку, формула которой должна быть скопирована.

2. Несколько копируемых ячеек необходимо отметить блоком.

3. Простейшее копирование выполняется «мышью»-указкой: взять за нижний правый угол курсора («мышь» выглядит как «+») и, удерживая левую кнопку мыши, протянуть ячейку в нужном направлении.

Перенос (перемещение) формул.

1. Выбрать курсором ячейку, формула которой должна быть перенесена.

2. Если ячеек несколько, отметить их блоком.

3. Простейшей перенос выполняется «мышью»-указкой: взять за границу курсора («мышь» выглядит как стрелка) и, удерживая левую кнопку мыши, перенести ячейку в нужном направлении.

Замечание 1. При сортировке и переносе формул происходит автоматическое динамическое смещение адресов по строкам и столбцам. Если какая-либо переменная является внешней для вашей таблицы, не забывайте заранее устанавливать в расчете ее абсолютный адрес.

Сортировка.

Сортировка – это перестановка строк таблицы по возрастанию или убыванию признака (показателя), который в данный момент вы анализируете. Этот признак называется «Ключ сортировки».

Для перемещения информации в таблице в нужном ключе необходимо указать блоком строки целиком, подлежащие перемещению.

Если шапка таблицы простейшего построения (нет подколонок), то включите и ее в выбираемый блок таблицы, тогда при сортировке вам будут предложены ключи из названий шапки, - это очень удобно.

Если в шапке есть структурные колонки, то перед сортировкой добавьте в таблице после шапки пустую строку. Включите и ее в выбираемый блок таблицы, тогда при сортировке вам будут предложены ключи из литерных обозначений колонок, вам придется самим сопоставлять обозначения и названия показателей.

Выполнение сортировки возможно двумя способами: 1) с помощью кнопок на панели инструментов, но их ключ - только первая колонка выбранного блока; 2) через команду «Данные» - «СОРТИРОВКА» – самый грамотный вариант работы.

Замечание 2. Сортировка информации является очень рискованным мероприятием, поэтому перед началом такой работы сохраните таблицу, желательно и на дискету тоже, и дискету уберите в несгораемый сейф.

Диаграммы.

Для построения диаграмм необходимо решить для себя два ключевых вопроса:

- какие данные хотим иллюстрировать?

- Какая диаграмма для этого более всего подходит?

Колонки с исходными данными(оклад, отработано дней, дней по больничному листу) и промежуточными расчетами лучше всего изображать столбиковыми гистограммами, так как данная информация является первичной и дискретной.

Данные для диаграммы отмечаются блоком и вызывается «Мастер диаграмм».

Для правильного оформления необходимо пройти все этапы построения диаграммы. Если пунктов анализа много – более 30, то имеет смысл поместить диаграмму на отдельном листе расчетной книги, но не забывать об этом при печати.

Замечание 3. При построении столбиковых гистограммах важно помнить, что таблица и диаграмма обладают прямой и обратной связью: с одной стороны изменение исходных данных таблицы, влечет ее перерасчет и изменение внешнего вида иллюстрации; с другой – изменение величины столбиков рисунка вносит коррективу в исходные данные таблицы, меняет результат расчетов. Поэтому будьте осторожны при оформлении внешнего вида вашей диаграммы.

Для построения сравнительной диаграммы двух и более показателей (например сравнение оклада и суммы к получению) разрозненные колонки таблицы отмечаются сочетанием: клавиша CTRL и указатель мышки.

Пояснительная записка к расчету составляется в текстовом редакторе. Она содержит сообщение кем, когда и где выполнен расчет, на основании каких документов и распоряжений.

К пояснительной записке должна быть приложена ведомость начисления, содержащая графы:

- Табельный номер;

- ФИО;

- Сумма к получению;

- Подпись лица, получившего деньги в кассе.

Желаю успеха!

Лабораторная работа №3

Тема:Средние величины в статистике

Цель работы: получить навыки построения рядов распределения и расчета средних величин.

План:

1. Рассмотреть виды распределений.

2. Структурные средние величины.

3. Средние арифметические.

4. Средние гармонические.

5. Средние геометрические

6. Средние геометрические.

Задание:

1. Построить дискретный ряд распределения сотрудников предприятия по группам начисления, распределив сотрудников в группах по величине оклада. Провести полное исследование ряда. Рассчитать средний оклад по предприятию и по каждой группе. Снабдить расчеты иллюстрациями и комментариями.

2. Построить дискретный ряд распределения по возрастанию совокупного начисления сотрудникам предприятия, образовав пять равных интервалов. Провести полное исследование ряда. Рассчитать средний оклад по предприятию и по каждой группе. Снабдить расчеты иллюстрациями и комментариями.

Теоретический материал:

Для выполнения работы рекомендуется использовать электронные таблицы Microsoft EXCEL, Microsoft Word для OFFICE 97,98,2000 и созданную в предыдущей работе таблицу.

Группировка – разбиение элементов генеральной совокупности на основании главного изучаемого признака с дальнейшим объединением элементов в группы по тому же признаку.

Ряд распределения – это сгруппированная упорядоченная информация по главному изучаемому признаку.

Если подлежащее группировки – альтернативный признак, то ряд распределения – дискретный, иначе – если показатель непрерывный или множественный, то ряд распределения для него – интервальный.

Ряды распределения оформляются в таблице и иллюстрируются графиками.

Подлежащим ряда является группировочный признак, обозначается в расчетах переменной x_i,где i – счетчик групп, количество которых обозначим переменной целой n. Следующий показатель ряда – это количество элементов генеральной совокупности, попавших в ту или иную группу (частота), обозначим переменной f_i. Перечисленные выше показатели являются абсолютными статистическими величинами, так как выражаются в принятых единицах измерения.

Следующий показатель – это показатель структуры – доля (или частость) численности элементов каждой группы в общем объеме распределения. Если численность элементов каждой текущей группы - f_i, количество групп - n, общая численность элементов 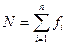, то доля текущей группы - 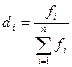- безразмерная величина, может быть выражена в долях. Тогда общее множество составляет 1, либо в процентах, тогда общее число элементов – 100%. Результаты долевых расчетов необходимо округлять очень аккуратно так, чтобы сумма всех долей равнялась точно единице. В большую сторону округлять имеет смысл наименьшие результаты, а в меньшую – наибольшие.

Структуру экономического процесса наилучшим образом иллюстрирует круговая диаграмма, где можно особо указать долю альтернативного признака.

Альтернативный признак – это совокупность значений изучаемого показателя, удовлетворяющих определенному условию либо вызывающих особый интерес у исследователя. Например, среди всех студентов, сдавших сессию с различными результатами, наибольший интерес у деканата вызывают студенты, сдавшие сессию на «хорошо» и «отлично».

Интенсивность нарастания элементов генеральной совокупности по нарастанию изучаемого признака показывает кумулята процесса – абсолютная статистическая величина, которая для каждой текущей группы рассчитывается как сумма всех предыдущих частот, включая частоту текущей группы. Кумулята – непрерывный показатель, потому ее изображают непрерывной ломаной линией.

Структурные средние величины распределения позволяют проанализировать его нормальность: чем ближе друг к другу мода, медиана и средняя арифметическая, тем ближе исследуемый ряд распределения к нормальному.

Мода – значение изучаемого признака в распределении с наивысшей частотой. Если наибольшую частоту имеют две и более группы, то распределение называется бимодальным.

Медиана – значение изучаемого признака, которое имеет средний по распределению элемент.

Средняя арифметическая величина - одна из разновидностей средних степенных, когда показатель степени равен единице. По генеральной совокупности в целом используется простая средняя арифметическая: 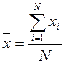. В дискретных рядах используется средняя арифметическая взвешенная: 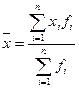. Перечисленные формулы используются, если информация представлена в явном виде.

Если известны обратные величины анализируемому показателю, то используется формула средней гармонической и средней гармонической взвешенной. Этот показатель рассчитывается из общей формулы средней степенной при показателе степени к=-1. Для генеральной совокупности в целом: ,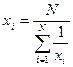

для дискретного ряда распределения - .

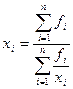В интервальных рядах распределения очень важно правильно выбрать количество интервалов. Для небольшой численности генеральной совокупности (N<200), число интервалов n должно находиться в диапазоне от 4 до 7. При N>200 полезно пользоваться формулой Стерджесса сглаженного роста числа интервалов относительно роста численности элементов исследования: n = 1 + 3,322LgN.

Длина интервалов может быть величиной постоянной, в этом случае ряд распределения равномерный. Пустые интервалы в распределении не допускаются, в случае такой ситуации выбирается новое число интервалов либо границы интервалов раздвигаются, и распределение становится неравномерным. В таблицу распределения кроме частоты добавляются колонки с длинами интервалов и их центрами.

Крайние интервалы могут быть неопределенными без четкой нижней или верхней границы. Параметры таких интервалов рассчитываются через определенные рядом стоящие.

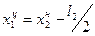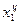Например, центр первого неопределенного интервала: , где - центр первого (младшего или нижнего интервала); 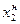- нижняя граница второго интервала, l₂ – длина второго интервала.

Для интервальных рядов распределения кроме частости рассчитывается плотность распределения как отношение частоты к длине интервала; плотность показывает концентрацию элементов совокупности по интервалам.

Замечание 1. По правилам умолчания интервалы распределения являются полуоткрытыми: нижняя граница включается в интервал, а верхняя – исключается. В процессе распределения единиц по интервалам, значение, попавшее на границу, относится к старшему (следующему) интервалу.

Замечание 2. Важно следить за тем, что бы критическое значение изучаемого признака выходило на границу интервала. Например, 100% выполнения плана должно быть нижней границей верхнего интервала.

Структурные средние величины рассчитываются по формулам:

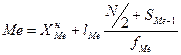, где S_Mе-1 – значение кумуляты на предыдущем перед медианным интервале.

.

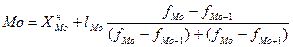Структурные средние величины могут быть найдены из графиков, но для этого очень важно подобрать масштаб и вычертить функции четко.

Средняя арифметическая в интервальных рядах рассчитывается через центры интервалов: 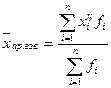; гармоническая взвешенная: .

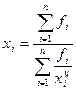Средняя геометрическая используется для усреднения относительных величин, таких как темпы роста, темпы прироста, индексы. Пример их вычислений рассмотрим в лабораторной работе №6.

Средняя квадратическая используется для оценки качества средней арифметической величины, и ее использование будет рассмотрено в следующей работе

Удачи в расчетах!

Лабораторная работа №4