Кафедра «Прикладная математика и эконометрика»
Санкт-петербургскИЙ государственнЫЙ УНИВЕРСИТЕТ сервиса и экономики
Кафедра «Прикладная математика и эконометрика»
О.Ю.Тарасова
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ В СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО КОНТРОЛЬНОЙ РАБОТЕ
для студентов направления 080506.65 специальности «логистика и управление цепями поставок»,
Всех форм обучения
Санкт-Петербург
Одобрено на заседании кафедры ПМиЭ, протокол №
Экономико-математические методы и модели в социально-экономических исследованиях. Методические указания по контрольной работе для студентов направления 080506.65 специальности «Логистика и управление цепями поставок», всех форм обучения. - СПб.: Изд-во СПбГУСЭ, 2011. – 17 с.
Сборник содержит задачи для контрольных работ и методические указания для их выполнения по всем разделам данной дисциплины, предусмотренной учебным планом специальности «» в соответствии с Государственным образовательным стандартов II поколения.
Каждая контрольная работа состоит из задач одного или нескольких разделов данного сборника, выбранных в соответствии с рабочей программой.
Составители: канд. тех. наук, доц. О.Ю.Тарасова.
© Санкт-Петербургский государственный университет сервиса и экономики
2011 г.
Содержание
Требования к оформлению контрольных работ......................................4
Формирование исходных данных к задачам...........................................5
Раздел 1. Элементы математической статистики..................................6
Раздел 2. Элементы регрессионного анализа.........................................7
Раздел 3. Линейное программирование…..............................................7
Раздел 4. Элементы теории игр…….....................................................10
Раздел 5. Сетевое планирование…………….......................................11
Раздел 6. Системы массового обслуживания (СМО)……..................12
Раздел 7. Модель межотраслевого баланса (модель Леонтьева).......13
Краткое содержание (программа) курса................................................14
Список учебной литературы ..................................................................16
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название Университета; название кафедры; название и номер контрольной работы; название (номер) специальности; фамилию,имя, отчество и личный шифр студента.
2. На каждой странице надо оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу.
3. Условия задач переписывать полностью необязательно, достаточно указать номер задачи по данному сборнику. В условия задач надо сначала подставить конкретные числовые значения параметров т и п, и только после этого приступать к их решению.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Формирование исходных данных к задачам
Каждая контрольная работа состоит из задач одного или нескольких разделов сборника.
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовых данных параметров т и п определяются по двум последним цифрам своего шифра (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | ||||||||||
| т |
Таблица 2 (выбор параметра п )
| В | ||||||||||
| п |
Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т = 4, п = 1. Полученные т = 4 и п = 1 подставляются в условия всех задач контрольной работы этого студента.
1. Элементы математической статистики
Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб.:
| № предприятия | Выпуск продукции | Прибыль | № предприятия | Выпуск продукции | Прибыль |
| 60+n | 15,7 | 52,0 | 14,6 | ||
| 78,0 | 18,0 | 62,0 | 14,8 | ||
| 41,0 | 12,1 | 69,0 | 16,1 | ||
| 54,0 | 13,8 | 85,0 | 16,7 | ||
| 60+n | 15,5 | 70+n | 15,8 | ||
| n•m+20 | n+m+10 | 71,0 | 16,4 | ||
| 45,0 | 12,8 | n•m+30 | n+m+20 | ||
| 57,0 | 14,2 | 72,0 | 16,5 | ||
| 67,0 | 15,9 | 88,0 | 18,5 | ||
| 80+n | 17,6 | 70+n | 16,4 | ||
| 92,0 | 18,2 | 74,0 | 16,0 | ||
| 48,0 | n+m+5 | 96,0 | 19,1 | ||
| 59,0 | 16,5 | 75,0 | 16,3 | ||
| 68,0 | 16,2 | 101,0 | 19,6 | ||
| 80+n | 16,7 | 70+n | 17,2 |
По исходным данным:
Задание 1.1.
1.1.1.Построение статистического ряда распределения и расчета числовых характеристик ряда предприятий по сумме прибыли.
1.1.2.Рассчитайте числовые характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую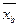 
, среднее квадратическое отклонение 
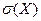, дисперсию, коэффициент вариации V. Сделайте выводы.
Задание 1.2.
1.2.1.Определите границы, в которых с вероятностью 0,997 заключена сумма прибыли одного предприятия в генеральной совокупности.
1.2.2. Используя c2-критерий Пирсона, при уровне значимости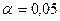 
проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
Задание 2.1.
2.1.1. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.
2.1.2. Полное исследование выборочного уравнения регрессии 
.
2.1.3. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.
При расчетах целесообразно использовать стандартные математические пакеты для персональных компьютеров.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.
ЭЛЕМЕНТЫ ТЕОРИИ ИГР.
4.1. Игра 
задана матрицей
Найти вероятности применения стратегий 1-м и 2-м игроком для получения цены игры. (Задачу решить аналитическим методом.)
4.2. Игра задана матрицами
для 
- четного
и
для - нечетного.
Применяя графический метод, найти смешанные оптимальные стратегии обоих игроков и определить цену игры.
СЕТЕВОЕ ПЛАНИРОВАНИЕ.
5.1. Прогресс производства сложной продукции разбивается на отдельные этапы, зашифрованные номерами 1, 2,..., 10. 1 – начальный этап производства продукции, 10 – завершающий. Переход от 
-го этапа к 
-му этапу назовем операцией. Возможны выполнения операций 
и их продолжительности 
задаются таблицей.
| N п/п | шифр операции | продолжительность операции | |
 | | ||
| 1→2 |  | ||
| 1→3 | |||
| 1→4 | | ||
| 2→3 | |||
| 2→6 | |||
| 4→3 | |||
| 4→6 | |||
| 3→5 | |||
| 3→7 |  | ||
| 5→9 |  | ||
| 6→7 | |||
| 6→8 | |||
| 7→8 | |||
| 7→9 | | ||
| 7→10 | |||
| 8→10 | |||
| 9→10 | |
5.1.1. Составьте и упорядочите по слоям сетевой график производства работ. Номера этапов необходимо обвести кружками, а операции обозначить стрелками, проставляя над ними продолжительность операции.
5.1.2. Считая, что начало работы происходит во время 
, определите время 
окончания каждого -го этапа и проставьте его над соответствующим кружком
5.1.3. Найдите критическое время завершения процесса работ Ткр и выделите стрелки, лежащие на критическом пути.
5.1.4. Для каждой некритической операции определите резервы свободного времени 
и проставьте их над стрелками рядом с в скобках.
5.1.5. Решите задачу табличным методом. Номера этапов, лежащие на критическом пути подчеркните. (В табличном методе кроме резервов свободного времени необходимо также найти полные резервы времени 
для каждого этапа.)
6. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ (СМО).
6.1. В парикмахерский салон приходит в среднем 
клиента в час (т.е. интенсивность 
поступления заявок в систему равна 
/час), а среднее время обслуживания одного клиента равно 1/ часов. Содержание одного рабочего места обходится в тысяч рублей за 1 час, а доход от обслуживания одного клиента составляет 
тысяч рублей в час.
6.1.1. Найти относительную пропускную способность СМО 
(т.е. вероятность того, что поступившая заявка будет обслужена) и абсолютную пропускную способность СМО 
(число заявок, обслуживаемых за 1 час), если салон обслуживает два мастера.
6.1.2. Найти доход 
, полученный за 1 час работы двух мастеров.
6.1.3. Найти аналогичные характеристики СМО 
, 
и 
, когда салон обслуживают три мастера, и определить, выгодно ли принять на работу третьего мастера с точки зрения общего дохода, полученного за 1 час работы салона.
МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА (МОДЕЛЬ ЛЕОНТЬЕВА).
7.1. Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязь определяет матрица А коэффициентов прямых затрат
,
в которой число 
, стоящее на пересечении -ой строки и -го столбца равно 
, где 
– поток средств производства из -ой отрасли в -ую, а 
– валовой объем продукции -ой отрасли (все объемы продукции выражаются в единицах стоимости).
Задан также вектор 
объемов конечной продукции.
7.1.1. Составить уравнение межотраслевого баланса.
7.1.2. Решить систему уравнений межотраслевого баланса, то есть найти объемы валовой продукции каждой отрасли 
обеспечивающие потребности всех отраслей и изготовление конечной продукции Y. (Расчеты рекомендуется производить с точностью до двух знаков после запятой)
7.1.3. Составить таблицу Х потоков средств производства .
7.1.4. Определить общие доходы каждой отрасли 
.
7.1.5. Результаты расчетов оформить в виде таблицы межотраслевого баланса:
 потребляющие отрасли отрасли производящие | I | II | III | конечный продукт | валовой продукт |
| I |  |  |  |  |  |
| II |  |  |  |  |  |
| III |  |  |  |  |  |
| общий доход |  |  |  | ||
| валовой продукт | | | |
7.1.6. Найти матрицу коэффициентов полных затрат по формуле 
, где Е – единичная матрица размера 
.
Краткое содержание (программа) курса
Линейное программирование.
Общая и основная задачи линейного программирования (ЛП). Основные теоремы ЛП. Геометрический метод решения задач ЛП. Симплек-метод: определение первоначального допустимого базисного решения; проверка решения на оптимальность; переход к другому допустимому решению. Двойственные задачи: их свойства; теоремы двойственности; объективно обусловленные оценки и их смысл. Транспортная задача: экономико-математическая модель транспортной задачи; нахождение первоначального базисного распределения поставок (метод «северо-западного» угла, метод наименьших затрат); критерий оптимальности базисного распределения поставок; перераспределение поставок; вырождение транспортной задачи; открытая модель транспортной задачи. Взаимно двойственные задачи линейного программирования.
Элементы теории игр.
Основные понятия теории игр; антагонистические игры, платежная матрица; решение игр в смешанных стратегиях; геометрические решения игр размера 2xn, mx2; приведение матричной игры к задаче ЛП.
5. Сетевое планирование.
Управление запасами: основные понятия; модель производственных поставок; модель поставок со скидкой. Модели динамического программирования: общая постановка задачи; принцип оптимальности и уравнения Беллмана; задача о распределении средств между предприятиями.
Список учебной литературы
1. И.П.Алдохин. Теория массового обслуживания в промышленности.— М.: Экономика,1980.
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие – М: Высшая школа. 2003.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учебное пособие: М.Высшее образование, 2006.
4. . Бугров,Я.С, Никольский С.М,; Высшая математика: Учеб. для вузов: В 3 т. / . Под ред. В. А. Садовничего. — 6-е изд., стереотип. — М.: Дрофа, 2004
5. Данко П.Е. , Попов А.Г.,.Кожевникова Т.Я . Высшая математика в упражнениях и задачах. Том 1,2.—М.:Высшая школа, 2000.
6. Ильин В.А., Позняк Э.Г.. Линейная алгебра.—Физматлит, 2002, 320 с.
7. Исследование операций в экономике: учебное пособие /под. ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2004 г.
8. Колемаев В.А. Теория вероятностей и математическая статистика. ИНФРА-М,1997.
9. Кузнецов Б.Т. Математические методы и модели исследования операций.-М.:ЮНИТИ-ДАНА, 2008.-309 с.
10.Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики.-СПб.:Питер, 2010.-496 с.
11.Красс М.С., Чупрынов Б.П. Математика для экономистов.- СПб.:Питер, 2005.-464 с.
12.Краснов М.Л., Киселев А.И., Макаренко Г., Функции комплексного переменного. Задачи и примеры с подробными решениями, Москва, УРСС, 2006
13.М.Л.Краснов, А.И.Киселев, Г.Н. Макаренко. Функции комплексного переменного. Операционное исчисление. Теория устойчивости.— М.: Наука, 2003. 180 с
14.Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов. – М.: ЮНИТИ-ДАНА, 2004. - 456 с.
15.Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике.1 курс.-М.:Айрис-пресс.2009.-592 с.
16.Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике.2 курс.-М.:Айрис-пресс.2009.-592 с.
17.Практикум по высшей математике для экономистов: учебное пособие, /под.ред.Н.Ш.Кремера.-М.:ЮНИТИ-ДАНА,2004.-423 с.
18.Привалов И.И. Ряды Фурье.- М.:Либроком, 2011, 168 с.
19.Пискунов Н.С.. Дифференциальное и интегральное исчисления Том 1,2.— М.: Наука, 1988.
20.Романовский. П.Н. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа.—М.: Наука, 1986.
21.Соколов А.В, Токарев В.В. Методы оптимальных решений (в двух томах). М.:-Физматлит.-2011, 564 с.
Санкт-петербургскИЙ государственнЫЙ УНИВЕРСИТЕТ сервиса и экономики
Кафедра «Прикладная математика и эконометрика»
О.Ю.Тарасова