Уравнения, допускающие понижение порядка
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВЫСШИХ ПОРЯДКОВ
Основные понятия
Определение.Обыкновенным дифференциальным уравнением 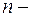 го порядка называется уравнение
го порядка называется уравнение
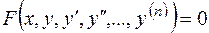 (2.1)
(2.1)
или, в разрешенном относительно старшей производной 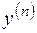 виде
виде
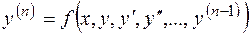 . (2.2)
. (2.2)
Определение. Всякая функция 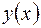 , имеющая непрерывные производные до порядка
, имеющая непрерывные производные до порядка 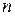 и удовлетворяющая уравнению (2.1) или (2.2), называется решением (частным решением) этого уравнения.
и удовлетворяющая уравнению (2.1) или (2.2), называется решением (частным решением) этого уравнения.
Определение.Задача нахождения решений дифференциального уравнения называется задачей интегрирования дифференциального уравнения.
Определение.Задачей Коши для дифференциального уравнения (2.2) называется задача отыскания решения 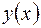 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям
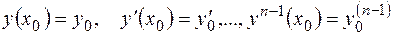 , (2.3)
, (2.3)
где 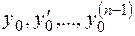 - заданные числа.
- заданные числа.
Определение.Общим решением уравнения (2.1) или (2.2) называется такая функция, 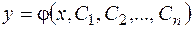 , которая при любых допустимых значениях параметров
, которая при любых допустимых значениях параметров 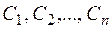 является решением этого дифференциального уравнения, и для любой задачи Коши с условиями (2.3) найдутся постоянные
является решением этого дифференциального уравнения, и для любой задачи Коши с условиями (2.3) найдутся постоянные 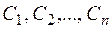 , определяемые из системы уравнений
, определяемые из системы уравнений
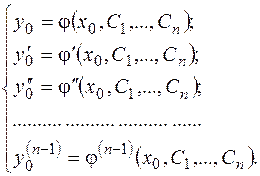 (2.4)
(2.4)
Определение.Уравнение
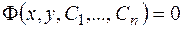 , (2.5)
, (2.5)
определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Пример.Показать, что функция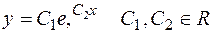 ,является решением дифференциального уравнения
,является решением дифференциального уравнения 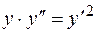 .
.
Решение.
1) Найдем 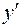 и
и 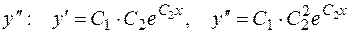 .
.
2) Подставив выражения для 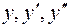 в данное уравнение, получим тождество
в данное уравнение, получим тождество
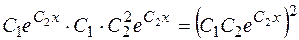 .
.
Следовательно, функция 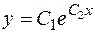 есть решение данного уравнения.
есть решение данного уравнения.
Определение.Решение уравнения (2.1) или (2.2), в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением.
Особое решение не может быть получено из общего ни при каких значениях 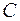 (включая и
(включая и 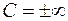 ).
).
2.1.1. Примеры для самостоятельного решения
Показать, что данные функции являются решениями соответствующих дифференциальных уравнений.
1. 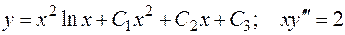 .
.
2. 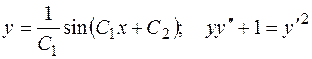 .
.
3. 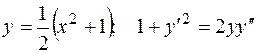 .
.
Уравнения, допускающие понижение порядка
Рассмотрим три наиболее распространенных вида дифференциальных уравнений  - го порядка, допускающих понижение порядка.
- го порядка, допускающих понижение порядка.
2.2.1.Уравнение вида
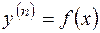 . (2.6)
. (2.6)
Общее решение получается с помощью 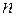 - кратного интегрирования
- кратного интегрирования
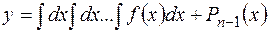 ,
,
где 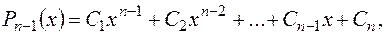 т.е. общий интеграл уравнения (2.6) есть сумма какого-либо частного решения этого уравнения и многочлена
т.е. общий интеграл уравнения (2.6) есть сумма какого-либо частного решения этого уравнения и многочлена 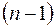 -й степени с произвольными постоянными коэффициентами.
-й степени с произвольными постоянными коэффициентами.
Пример. Найти общее решение уравнения 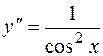 и его частное решение, удовлетворяющее условиям
и его частное решение, удовлетворяющее условиям 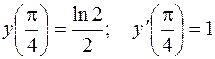 .
.
Решение.
1) Интегрируя первый раз, получим 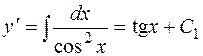 . После повторного интегрирования будем иметь
. После повторного интегрирования будем иметь
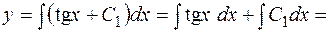
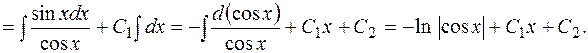
Следовательно, 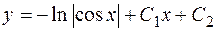 - общее решение.
- общее решение.
2) Чтобы найти частное решение, подставим в полученное общее решение и в выражение для первой производной значения 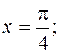
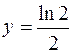 и
и 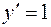 , получим систему двух уравнений с неизвестными
, получим систему двух уравнений с неизвестными 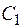 и
и 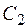 :
:
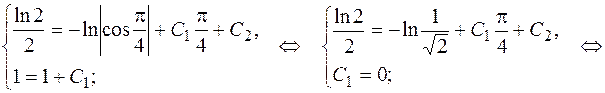
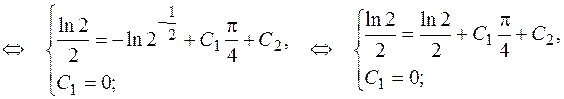
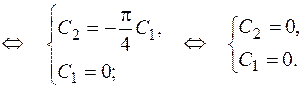
Подставив найденные 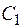 и
и 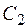 в общее решение получим искомое частное решение
в общее решение получим искомое частное решение 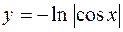 .
.
2.2.2.Уравнение вида
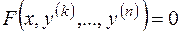 . (2.7)
. (2.7)
Уравнение (2.7) не содержит функции 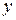 и ее нескольких последовательных производных
и ее нескольких последовательных производных 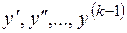 . С помощью замены
. С помощью замены 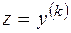 понизим порядок уравнения на
понизим порядок уравнения на 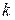 единиц:
единиц:
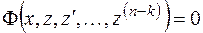 .
.
Предположим, что для полученного уравнения общее решение имеет вид
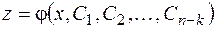 .
.
Тогда искомая функция 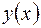 получается с помощью
получается с помощью 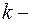 кратного интегрирования функции
кратного интегрирования функции 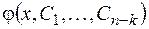 (см. п. 2.2.1.).
(см. п. 2.2.1.).
Пример.Найти общее решение уравнения 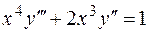 .
.
Решение.Данное уравнение не содержит 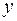 и
и 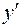 . Положим
. Положим 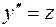 , тогда
, тогда 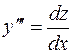 и уравнение будет иметь вид:
и уравнение будет иметь вид: 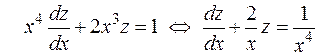 . Это линейное уравнение первого порядка (см. п.1.4.). Его общее решение имеет вид
. Это линейное уравнение первого порядка (см. п.1.4.). Его общее решение имеет вид 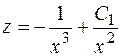 . Так как
. Так как 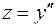 , то для отыскания искомого общего решения надо проинтегрировать уравнение
, то для отыскания искомого общего решения надо проинтегрировать уравнение 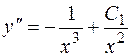 . Таким образом,
. Таким образом,
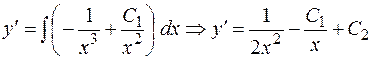 ,
,
тогда
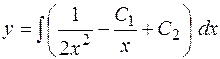 .
.
Следовательно, 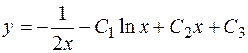 , где
, где 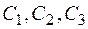 - произвольные постоянные, является общим решением заданного уравнения.
- произвольные постоянные, является общим решением заданного уравнения.
2.2.3.Уравнения вида
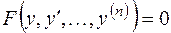 . (2.8)
. (2.8)
Уравнение (2.8) не содержит явно независимую переменную 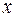 . В этом случае примем
. В этом случае примем 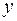 за независимую переменную и введем новую функцию
за независимую переменную и введем новую функцию 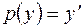 . Считая, что
. Считая, что 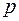 есть функция от
есть функция от 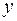 и через посредство
и через посредство 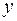 зависит от
зависит от 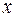 и, применяя правило дифференцирования сложных функций, получим для производных от
и, применяя правило дифференцирования сложных функций, получим для производных от 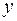 по
по 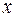 выражения
выражения
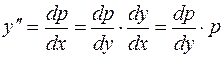 ,
,
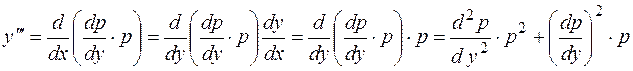 ,
,
аналогично вычисляются 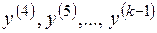 .
.
Подставляя в уравнение (2.8) вместо 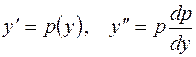 и т.д., увидим, что в новых переменных порядок уравнения будет
и т.д., увидим, что в новых переменных порядок уравнения будет 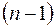 , т.е. на единицу ниже.
, т.е. на единицу ниже.
Если это преобразованное уравнение проинтегрировано и 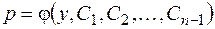 - его решение, то нахождение общего интеграла данного уравнения сводится к интегрированию
- его решение, то нахождение общего интеграла данного уравнения сводится к интегрированию
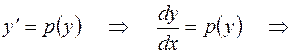
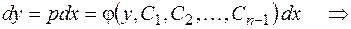
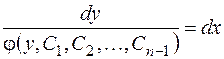 .
.
Откуда получаем общее решение ОДУ (2.8)
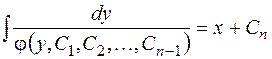 .
.
Одна из произвольных постоянных 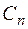 входит в качестве слагаемого к
входит в качестве слагаемого к 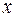 , а это означает, что всякую интегральную кривую можно перемещать параллельно оси
, а это означает, что всякую интегральную кривую можно перемещать параллельно оси 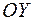 .
.
Пример.Найти общий интеграл уравнения 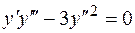 .
.
Решение.Положим
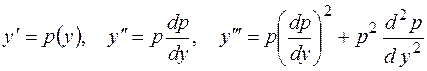 и подставим в исходное уравнение, тогда получим
и подставим в исходное уравнение, тогда получим
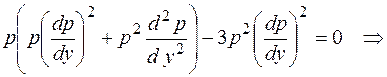
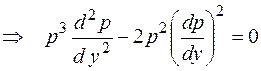 .
.
Сократим на 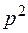 , при этом учтем теряемое решение
, при этом учтем теряемое решение 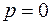 или
или 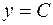 и получим
и получим
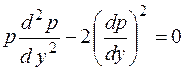 .
.
Это уравнение рассматриваемого вида, делая ту же замену 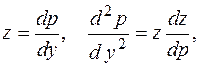 придем к уравнению
придем к уравнению
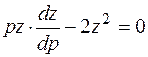 .
.
Сократив на 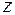 (при этом учитываем еще одно решение
(при этом учитываем еще одно решение 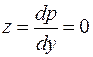 , т.е.
, т.е. 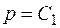 и
и 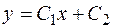 ), получим
), получим
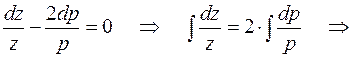
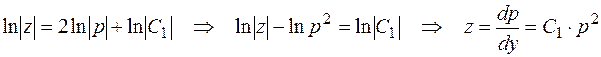 .
.
Проинтегрировав уравнение 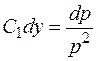 , находим
, находим 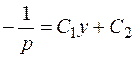 , или
, или 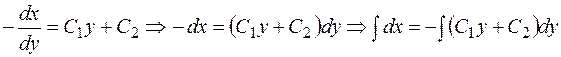 .
.
Окончательно получим
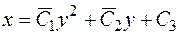 , где
, где 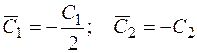 .
.
Это семейство парабол. Заметим, что в общее решение входят и потерянные ранее частные решения (кроме 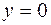 ).
).
2.2.4. Примеры для самостоятельного решения
Решить дифференциальные уравнения, используя методы понижения порядка.
1. 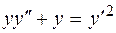 , 5.
, 5. 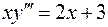 ,
,
2. 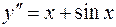 , 6.
, 6. 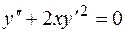 ,
,
3. 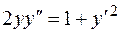 , 7.
, 7. 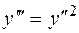 ,
,
4. 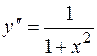 , 8.
, 8. 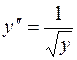 .
.
Порядков
Коэффициентами
Общий вид линейного дифференциального уравнения порядка 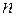 с постоянными коэффициентами есть
с постоянными коэффициентами есть
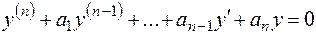 , (2.17)
, (2.17)
где 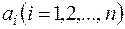 - действительные постоянные.
- действительные постоянные.
Определение.Уравнение
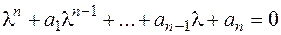 , (2.18)
, (2.18)
полученное заменой производных 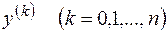 искомой функции степенями
искомой функции степенями 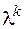 , называется характеристическим уравнением для уравнения (2.17).
, называется характеристическим уравнением для уравнения (2.17).
Каждому действительному корню 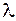 уравнения (2.18) кратности
уравнения (2.18) кратности 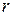 соответствуют
соответствуют 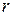 линейно независимых решений уравнения (2.17)
линейно независимых решений уравнения (2.17)
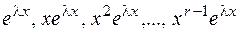 , (2.19)
, (2.19)
а каждой паре комплексных корней 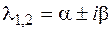 кратности
кратности 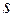 соответствуют
соответствуют 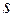 пар линейно независимых решений:
пар линейно независимых решений:
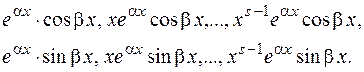 (2.20)
(2.20)
Запишем общее решение для случая 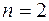 . Рассмотрим уравнение
. Рассмотрим уравнение
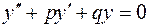 , (2.21)
, (2.21)
где 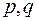 - действительные числа.
- действительные числа.
Характеристическое уравнение для (2.21) имеет вид
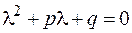 . (2.22)
. (2.22)
Если квадратное уравнение (2.22) имеет два различных действительных корня 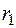 и
и 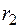 , то согласно (2.19) имеем два линейно независимых решения уравнения (2.21)
, то согласно (2.19) имеем два линейно независимых решения уравнения (2.21)
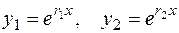 .
.
Общее решение имеет вид
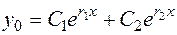 , (2.23)
, (2.23)
где 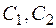 - произвольные постоянные.
- произвольные постоянные.
Если квадратное уравнение (2.22) имеет комплексные корни 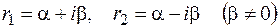 , тогда согласно (2.20) имеем два линейно независимых решения уравнения (2.21)
, тогда согласно (2.20) имеем два линейно независимых решения уравнения (2.21)
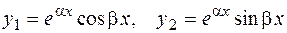 .
.
Общее решение имеет вид
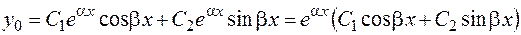 . (2.24)
. (2.24)
Если квадратное уравнение (2.22) имеет два равных действительных корня 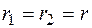 , то согласно (2.19) имеем два линейно независимых решения уравнения (2.21)
, то согласно (2.19) имеем два линейно независимых решения уравнения (2.21)
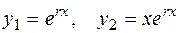 .
.
Общее решение уравнения имеет вид
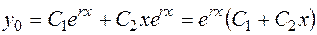 . (2.25)
. (2.25)
Примеры. Найти общее решение уравнений:
1. 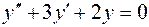 ;
;
2. 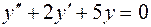 ;
;
3. 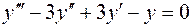 .
.
Решения.
1. Рассмотрим 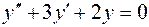 , его характеристическое урав-нение
, его характеристическое урав-нение 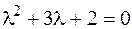 имеет корни
имеет корни 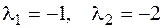 . Запишем фундаментальную систему решений
. Запишем фундаментальную систему решений 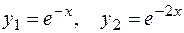 . Следовательно, общее решение имеет вид
. Следовательно, общее решение имеет вид 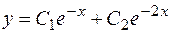 .
.
2. Для уравнения 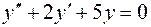 характеристическое уравне-ние имеет вид
характеристическое уравне-ние имеет вид 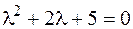 , его корни
, его корни 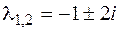 . Следовательно, функции
. Следовательно, функции 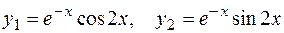 составляют фундаментальную систему решений, а общее решение имеет вид
составляют фундаментальную систему решений, а общее решение имеет вид 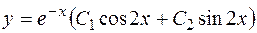 .
.
3. Уравнение 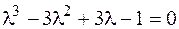 является характеристичес-ким для
является характеристичес-ким для 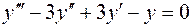 , его решением является
, его решением является 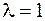 кратности
кратности 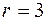 . Поэтому фундаментальная система решений имеет вид
. Поэтому фундаментальная система решений имеет вид 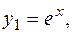

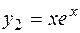 ,
, 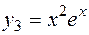 . Следовательно, общее решение исходного уравнения имеет вид:
. Следовательно, общее решение исходного уравнения имеет вид:
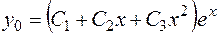 .
.
2.3.6. Примеры для самостоятельного решения
Найти общие решения дифференциальных уравнений.
1. 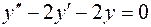 , , | 4. 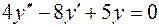 , , |
2. 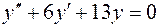 , , | 5. 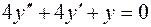 , , |
3. 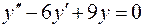 , , | 6. 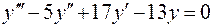 . . |
Коэффициентами
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами
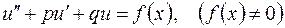 , (2.14)
, (2.14)
где 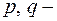 действительные числа.
действительные числа.
Общее решение этого уравнения записывается в виде 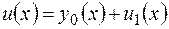 , где
, где 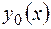 - общее решение соответствующего однородного уравнения (2.10),
- общее решение соответствующего однородного уравнения (2.10), 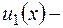 любое частное решение уравнения (2.14). Общее решение ОДУ (2.10)
любое частное решение уравнения (2.14). Общее решение ОДУ (2.10) 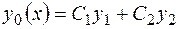 , для отыскания
, для отыскания 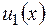 в общем случае используется метод Лагранжа вариации произвольных постоянных, рассмотренный в пункте 2.3.3.
в общем случае используется метод Лагранжа вариации произвольных постоянных, рассмотренный в пункте 2.3.3.
Пример.Найти общее решение уравнения
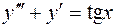 .
.
1. Решим однородное уравнение 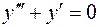 . Для чего запишем характеристическое уравнение
. Для чего запишем характеристическое уравнение 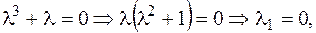
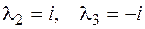 . Согласно (2.19), (2.20) фундаментальная система решений будет иметь вид
. Согласно (2.19), (2.20) фундаментальная система решений будет иметь вид 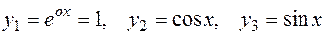 , следовательно, общее решение однородного уравнения
, следовательно, общее решение однородного уравнения
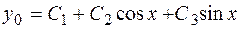 .
.
Для нахождения частного решения неоднородного уравнения воспользуемся методом вариации произвольных постоянных. Ищем частное решение в виде 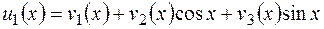 . Для определения
. Для определения 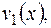
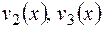 составим систему
составим систему
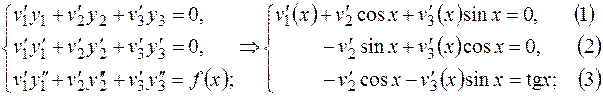
Умножив обе части второго уравнения на  , третьего - на
, третьего - на  и сложив, получим
и сложив, получим
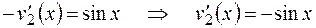 .
.
Подставив 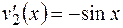 в уравнение (2), получим
в уравнение (2), получим
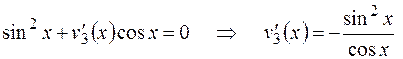 .
.
Сложив уравнения (1) и (3) будем иметь 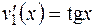 .
.
Интегрирование дает выражения для 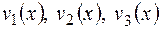 :
:
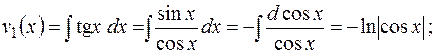
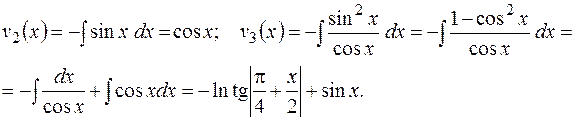
Итак, 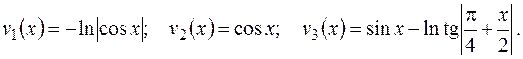
Учитывая, что 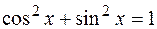 , получим искомое решение неоднородного уравнения
, получим искомое решение неоднородного уравнения
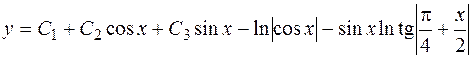 , где
, где 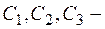 произвольные постоянные.
произвольные постоянные.
2.3.8. Примеры для самостоятельного решения
Методом Лагранжа вариации произвольных постоянных решить уравнения
1. 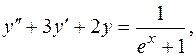 3.
3. 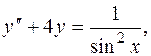
2. 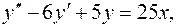 4.
4. 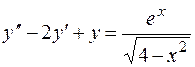 .
.
Основные понятия. Связь с дифференциальными
Уравнениями высших порядков
Выясним связь между системой дифференциальных уравнений первого порядка и одним уравнением высшего порядка. Если имеем, например, одно дифференциальное уравнение третьего порядка
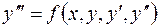 , (3.1)
, (3.1)
то, полагая 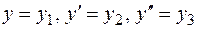 , можем заменить это уравнение третьего порядка системой трех уравнений первого порядка
, можем заменить это уравнение третьего порядка системой трех уравнений первого порядка
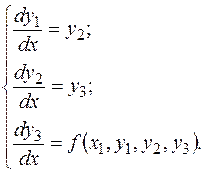 (3.2)
(3.2)
Уравнение третьего порядка (3.1) и система (3.2) равносильны в следующем смысле: если 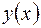 - решение уравнения третьего порядка, то
- решение уравнения третьего порядка, то 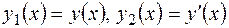 и
и 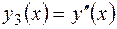 есть решение системы (3.2); а если
есть решение системы (3.2); а если 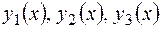 - решение системы, то
- решение системы, то 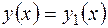 - решение уравнения третьего порядка (3.1).
- решение уравнения третьего порядка (3.1).
Аналогично, имея систему двух уравнений второго порядка
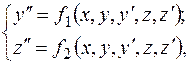 (3.3)
(3.3)
где 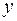 и
и 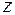 - искомые функции от
- искомые функции от 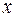 , мы можем заменить ее системой четырех уравнений первого порядка, вводя четыре неизвестные функции
, мы можем заменить ее системой четырех уравнений первого порядка, вводя четыре неизвестные функции 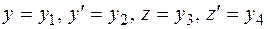 . Прежняя система (3.3) перепишется в виде
. Прежняя система (3.3) перепишется в виде
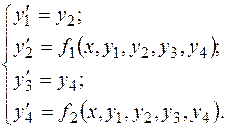
Можно показать, что, наоборот, интегрирование системы можно заменить интегрированием одного уравнения высшего порядка. Например, систему трех уравнений первого порядка
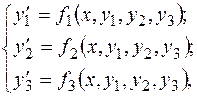
можно свести к уравнению третьего порядка относительно 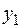 следующего вида
следующего вида
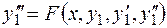 .
.
На этом основан метод решения систем дифференциальных уравнений –метод исключения неизвестных.
Пример.Рассмотрим систему первого порядка с двумя неизвестными 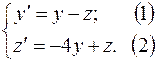
Решение. Используем метод исключения неизвестных, для чего из уравнения (1) выразим 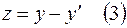 и продифференцируем полученное выражение:
и продифференцируем полученное выражение: 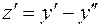 . Подставим найденные
. Подставим найденные 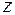 и
и 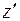 в уравнение (2):
в уравнение (2):
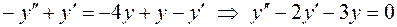 .
.
Последнее уравнение – это однородное линейное уравнение второго порядка с постоянными коэффициентами. Характеристическое уравнение 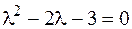 имеет корни
имеет корни 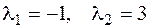 . Общее решение выписывается по формуле (2.23):
. Общее решение выписывается по формуле (2.23):
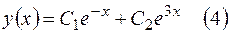 .
.
Из (3) находится 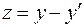 . Для чего, продифференцировав (4), получим
. Для чего, продифференцировав (4), получим 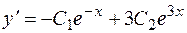 , следовательно,
, следовательно,
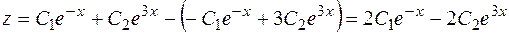 .
.
Таким образом, общее решение системы имеет вид
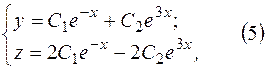
где 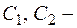 произвольные постоянные.
произвольные постоянные.
Здесь система из двух уравнений сведена к одному уравнению второго порядка.
Сформулируем основные понятия.
Определение.Система дифференциальных уравнений второго порядка вида
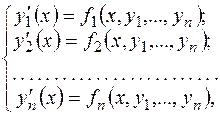 (3.4)
(3.4)
называется нормальной системой.
Определение. Решением системы (3.4) на интервале 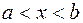 называется совокупность функций
называется совокупность функций 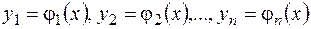 , непрерывно дифференцируемых на
, непрерывно дифференцируемых на 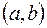 и обращающих уравнения системы (3.4) в тождества относительно
и обращающих уравнения системы (3.4) в тождества относительно 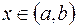 .
.
Определение.Интегралом нормальной системы (3.4) называется функция 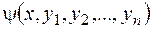 , определенная и непрерывная вместе с частными производными
, определенная и непрерывная вместе с частными производными 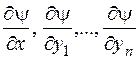 в некоторой области
в некоторой области 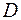 изменения переменных и принимающая при любых
изменения переменных и принимающая при любых 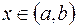 постоянное значение при подстановке в нее произвольного решения системы.
постоянное значение при подстановке в нее произвольного решения системы.
Определение.Равенство
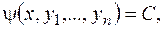
где 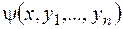 - интеграл нормальной системы, а
- интеграл нормальной системы, а 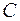 – произвольная постоянная, называется первым интегралом системы (3.4).
– произвольная постоянная, называется первым интегралом системы (3.4).
Дифференциальное уравнение 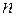 - го порядка
- го порядка
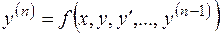
можно свести к нормальной системе (3.4). Обратно, система (3.4) в большинстве случаев сводится к дифференциальному уравнению 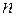 -го порядка, проинтегрировав которое можно найти и решение исходной системы.
-го порядка, проинтегрировав которое можно найти и решение исходной системы.
Задача Коши для системы (3.4) ставится следующим образом: найти решение 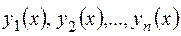 системы (3.4), удовлетворяющее начальным условиям
системы (3.4), удовлетворяющее начальным условиям
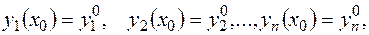 (3.5)
(3.5)
где 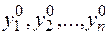 - заданные числа.
- заданные числа.
Определение.Общим решением системы (3.4) называется совокупность функций
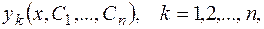 (3.6)
(3.6)
зависящих от 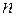 произвольных постоянных, которые при любых допустимых значениях постоянных
произвольных постоянных, которые при любых допустимых значениях постоянных 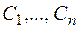 обращают уравнения системы (3.4) в тождества, и в области, в которой выполнены условия теоремы Коши, из совокупности функций (3.6) можно получить решение любой задачи Коши.
обращают уравнения системы (3.4) в тождества, и в области, в которой выполнены условия теоремы Коши, из совокупности функций (3.6) можно получить решение любой задачи Коши.
Пример. Показать, что определенная равенствами
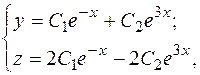 (1)
(1)
система функций является общим решением системы уравнений
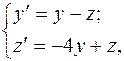 (2)
(2)
из предыдущего примера.
Решение. В качестве области 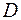 для (2) можно взять область
для (2) можно взять область 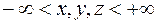 ; при этом для любых
; при этом для любых 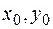 и
и 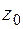 из этой области выполнены условия теоремы Коши. Подставив значения
из этой области выполнены условия теоремы Коши. Подставив значения 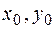 и
и 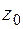 в систему (1), получим систему уравнений для определения
в систему (1), получим систему уравнений для определения 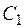 и
и 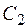 :
:
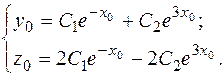
Определитель этой системы
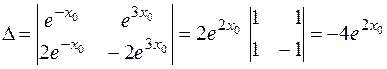 отличен от нуля при любом
отличен от нуля при любом 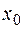 . Следовательно, при любых
. Следовательно, при любых 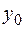 и
и 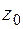 числа
числа 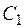 и
и 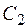 определяются однозначно, т.е. из системы функций (1) можно получить любое решение задачи Коши для системы дифференциальных уравнений (2).
определяются однозначно, т.е. из системы функций (1) можно получить любое решение задачи Коши для системы дифференциальных уравнений (2).
Пример. Найти общее решение системы дифференциальных уравнений
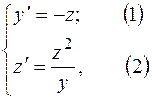
и частное решение, удовлетворяющее начальным условиям 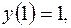
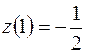 .
.
Решение.Продифференцируем обе части первого уравнения по 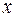 , получим
, получим
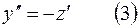 .
.
В уравнение (2) 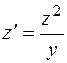 , подставим
, подставим 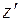 из (3):
из (3): 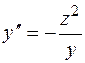 . Из уравнения (1) получим
. Из уравнения (1) получим 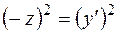 и, подставив
и, подставив 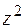 в
в 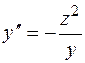 , будем иметь
, будем иметь 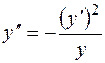 . Следовательно, система двух уравнений первого порядка свелась к одному уравнению второго порядка
. Следовательно, система двух уравнений первого порядка свелась к одному уравнению второго порядка
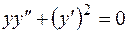 .
.
Заметим, что 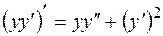 , поэтому последнее уравнение будет иметь вид:
, поэтому последнее уравнение будет иметь вид: 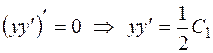 , откуда
, откуда 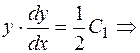
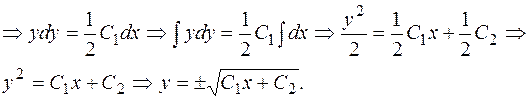
Из уравнения (1) имеем 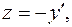 т.е.
т.е.
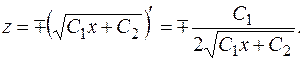
Итак, общее решение исходной системы имеет вид
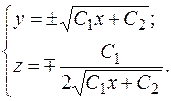
Для нахождения частного решения используем начальные условия 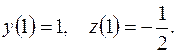 Подставив их в общее решение, получим систему для определения
Подставив их в общее решение, получим систему для определения 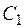 и
и 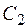 :
:
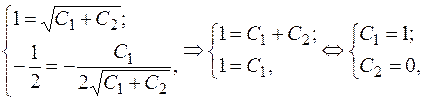
Подставив 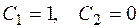 в общее решение системы, найдем искомое частное решение
в общее решение системы, найдем искомое частное решение
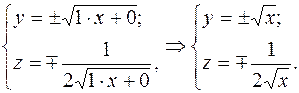
3.2. Примеры для самостоятельного решения
1. Найти общие решения систем дифференциальных уравнений.
 а)
а) 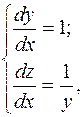 б)
б) 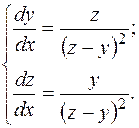
2. Найти общие решения систем дифференциальных уравнений, а также частные решения, удовлетворяющие заданным начальным условиям.
в) 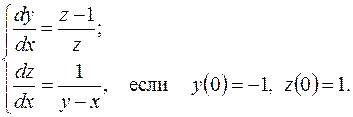
г) 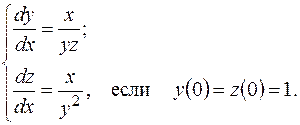
4. РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА ПО ТЕМЕ:
«Обыкновенные дифференциальные уравнения и
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВЫСШИХ ПОРЯДКОВ
Основные понятия
Определение.Обыкновенным дифференциальным уравнением 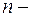 го порядка называется уравнение
го порядка называется уравнение
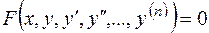 (2.1)
(2.1)
или, в разрешенном относительно старшей производной 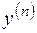 виде
виде
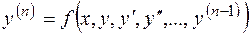 . (2.2)
. (2.2)
Определение. Всякая функция  , имеющая непрерывные производные до порядка
, имеющая непрерывные производные до порядка  и удовлетворяющая уравнению (2.1) или (2.2), называется решением (частным решением) этого уравнения.
и удовлетворяющая уравнению (2.1) или (2.2), называется решением (частным решением) этого уравнения.
Определение.Задача нахождения решений дифференциального уравнения называется задачей интегрирования дифференциального уравнения.
Определение.Задачей Коши для дифференциального уравнения (2.2) называется задача отыскания решения 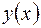 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям
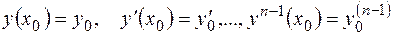 , (2.3)
, (2.3)
где 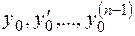 - заданные числа.
- заданные числа.
Определение.Общим решением уравнения (2.1) или (2.2) называется такая функция, 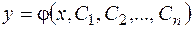 , которая при любых допустимых значениях параметров
, которая при любых допустимых значениях параметров 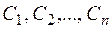 является решением этого дифференциального уравнения, и для любой задачи Коши с условиями (2.3) найдутся постоянные
является решением этого дифференциального уравнения, и для любой задачи Коши с условиями (2.3) найдутся постоянные 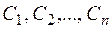 , определяемые из системы уравнений
, определяемые из системы уравнений
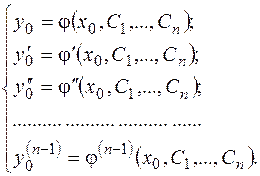 (2.4)
(2.4)
Определение.Уравнение
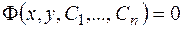 , (2.5)
, (2.5)
определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Пример.Показать, что функция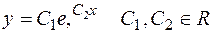 ,является решением дифференциального уравнения
,является решением дифференциального уравнения 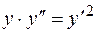 .
.
Решение.
1) Найдем 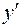 и
и 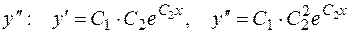 .
.
2) Подставив выражения для 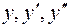 в данное уравнение, получим тождество
в данное уравнение, получим тождество
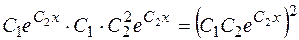 .
.
Следовательно, функция 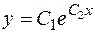 есть решение данного уравнения.
есть решение данного уравнения.
Определение.Решение уравнения (2.1) или (2.2), в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением.
Особое решение не может быть получено из общего ни при каких значениях 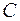 (включая и
(включая и 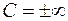 ).
).
2.1.1. Примеры для самостоятельного решения
Показать, что данные функции являются решениями соответствующих дифференциальных уравнений.
1. 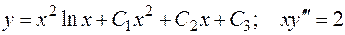 .
.
2. 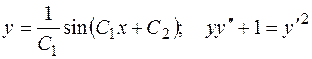 .
.
3. 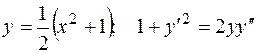 .
.
Уравнения, допускающие понижение порядка
Рассмотрим три наиболее распространенных вида дифференциальных уравнений 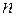 - го порядка, допускающих понижение порядка.
- го порядка, допускающих понижение порядка.
2.2.1.Уравнение вида
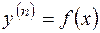 . (2.6)
. (2.6)
Общее решение получается с помощью 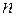 - кратного интегрирования
- кратного интегрирования
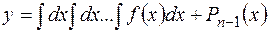 ,
,
где 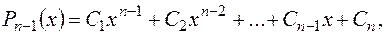 т.е. общий интеграл уравнения (2.6) есть сумма какого-либо частного решения этого уравнения и многочлена
т.е. общий интеграл уравнения (2.6) есть сумма какого-либо частного решения этого уравнения и многочлена 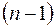 -й степени с произвольными постоянными коэффициентами.
-й степени с произвольными постоянными коэффициентами.
Пример. Найти общее решение уравнения 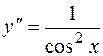 и его частное решение, удовлетворяющее условиям
и его частное решение, удовлетворяющее условиям 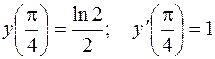 .
.
Решение.
1) Интегрируя первый раз, получим 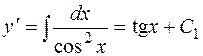 . После повторного интегрирования будем иметь
. После повторного интегрирования будем иметь
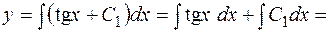
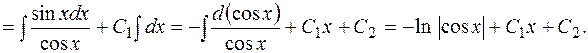
Следовательно, 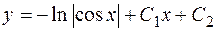 - общее решение.
- общее решение.
2) Чтобы найти частное решение, подставим в полученное общее решение и в выражение для первой производной значения 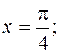
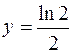 и
и 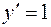 , получим систему двух уравнений с неизвестными
, получим систему двух уравнений с неизвестными 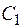 и
и 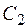 :
:
