Определение значимости эффектов.
1.½Ej½ < D, т. е. эффекты незначимы. Необходимо выполнить третий цикл и повторить п. п. 5.
2½Ej½ > D, т.е. эффекты значимы (или один из эффектов), и можно переходить к новой фазе.
Построение новой матрицы.
В качестве нулевой точки выбираем операционные условия предыдущей фазы с оптимальным выходом (например, точка 4 на рис.7.1). При переходе к новой фазе можно изменять величину интервалов варьирования и даже сами факторы. Новый план не обязательно должен быть квадратом. Он бывает и прямоугольником. Для второй фазы берем доверительный интервал эффектов из первой фазы, считая его априорно известным для фазы 2.
Таким образом, статистический анализ результатов при ЭВОП проводят последовательно после каждого цикла.
Следует иметь в виду, что фундаментальнейшим отличием промышленных экспериментов от лабораторных является экономический фактор. Поэтому цена за полученную информацию при ЭВОП не должна быть слишком большой (рост брака или разладка установок при экспериментах).
. Последовательное симплекс-планирование
Одним из экспериментальных методов, применяемых в промышленных условиях, является симплекс-планирование.
Этот метод был предложен в 1962 году Спендлеем, Некстом и Химсвортом.
Симплекс-планирование – это последовательное шаговое движение к оптимуму поверхности отклика. Для метода характерно совмещение изучения поверхности отклика и перемещения по ней. Это достигается тем, что эксперименты ставятся только в точках факторного пространства, соответствующих вершинам симплекса.
i-мерный симплекс представляет собой выпуклую фигуру, образованную i+1 точками(вершинами). Очевидно, что число вершин симплекса на единицу превосходит размерность факторного пространства. Так, на плоскости симплексом является треугольник, в трехмерном пространстве – тетраэдр, на одномерной оси – отрезок прямой.
Симплекс называется регулярным, если все расстояния между его вершинами равны. На плоскости – это равносторонний (правильный) треугольник. Неправильный симплекс можно всегда преобразовать в регулярный путем кодирования факторов по обычным формулам.
В основе применения симплекса для целей оптимизации лежит следующее его важное свойство: из любого симплекса можно, отбросив одну из вершин и используя оставшуюся грань, получить новый симплекс, добавив всего лишь одну точку (рис. 7.2). Из симплекса 1, 2, 3, отбросив точку 1 и используя грань 2-3, получаем новый симплекс 2, 3, 4, достроив точку 4.
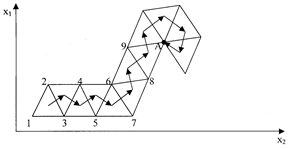 Рис. 4.2. Двумерный симплекс на плоскости |
Путем последовательного отбрасывания вершин можно осуществлять перемещение симплекса в факторном пространстве при каждом последующем эксперименте.
Если проводить эксперимент в вершинах симплекса, то можно найти направление максимального наклона поверхности отклика по результатам опытов. Оно проходит из центра симплекса через грань, противоположную вершине (выходу эксперимента) с “плохим” качеством. Это направление показано стрелками на рис. 4.2. Таким образом, отбрасывая точку с неудовлетворительным значением выхода, строим ее отражение и получаем новый симплекс.
Достигнув области экстремума, симплекс начинает вращаться вокруг своей точки с экстремальным значением выхода (точка А на рис.4.2), что определяет конец процесса оптимизации.
Среди различных методов построения исходных симплексов следует отметить два наиболее употребительных.
1-й вариант.
Одну из вершин симплекса помещают в начало кодированных координат. Остальные вершины располагают так, чтобы ребра, выходящие из первой вершины, образовывали одинаковые углы с координатными осями (рис. 4.3, а). Исходный план, составляющий i-мерный симплекс, ориентированный указанным образом, можно представить матрицей
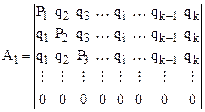, (4.8)
где
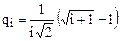, (4.9)
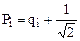, i = 1, 2, 3…k факторов. (4.10)
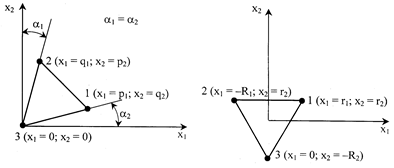 а) б) Рис.4.3. Построение начального симплекса: а – по варианту 1 (матрица А1); б – по варианту 2 (матрица А2) |
При использовании матрицы необходимо выделить часть, содержащую i-столбцов (факторов) и (i+1)-строк (вершин симплекса). Каждая строка матрицы соответствует одному эксперименту. Точка в начале координат имеет координаты ноль по всем осям.
2-й вариант.
В начало координат помещают центр симплекса, а одну из вершин располагают на одной из осей (рис.7.3,б). Тогда координаты вершин симплекса определяются матрицей
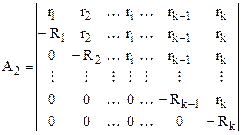, (4.11)
где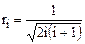 
, (4.12)
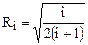, i = 1, 2, 3…k. (4.13)
Изменив в матрице знаки на противоположные, получим симплекс, симметричный данному относительно начала координат. Число опытов в симплексной матрице равно числу вершин симплекса.
Для практического пользования матрицей удобнее представить ее в численных значениях (например, для пяти факторов):
.
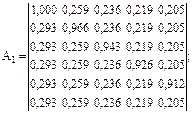
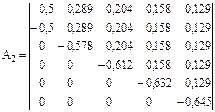Основными преимуществами симплексного планирования являются:
- значительное сокращение числа экспериментов;
- отсутствие нарушения общего движения к оптимуму при неправильной ориентации одного из симплексов, вызванной ошибкой опыта;
- возможность добавлять в процессе реализации плана дополнительный фактор.
В последнем случае требуется дополнительный опыт.
К недостаткам симплекс–планов следует отнести невозможность предварительной разработки экспериментальных планов и корректировки интервалов варьирования в ходе экспериментов; подготовку последующей серии экспериментов только после реализации предыдущей; ограниченную информацию о характере поверхности отклика.
Рассмотрим на численном примере последовательность этапов симплекс–планирования экстремальных экспериментов.
1. Постановка задачи исследования.
Пример:
Оптимизация геометрии концевых фрез.
2. Выбор выхода (отклика).
Пример:
Стойкость фрез Т в мин.
3. Выбор переменных факторов.
Пример:
задний угол a в градусах,
передний угол g в градусах,
ширина ленточки f в мм.
4. Определение возможной точности измерения и задания факторов.
Пример:
Da = ±5¢;
Dg = ±5¢;
Df = 0,005 мм.
5. Установление исходных данных: базового уровня (центра начального симплекса) и интервалов варьирования факторов.
Величина основного уровня i-го фактора в натуральных переменных xi0 соответствует среднему арифметическому исследуемых уровней фактора.
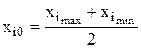. ( 4.14)
Величины предельных значений исследуемых факторов (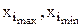 
) устанавливают на основе априорных данных или опыта и интуиции исследователя.
Интервалы варьирования Dxi должны примерно на порядок превосходить возможные ошибки измерений факторов (п.4). С базой (нулевым уровнем) xi0 интервалы варьирования связаны выражением
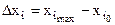. ( 4.15)
Пример: табл. 4.1.
Таблица 4.1
Исходные данные симплекс–плана
| Обозначение факторов | Размерность | База | Интервал варьирования | |
| натуральное | кодовое | |||
| a | x1 | град | ||
| g | x2 | град | ||
| f | x3 | мм | 0,5 | 0,3 |
6. Определение координат начального симплекса в кодовых переменных.
Для этого строится матрица исходного симплекса, которая является планом первой серии экспериментов.
Пример: 3-факторное симплекс–планирование.
.
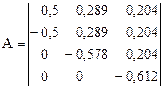7. Переход от кодовых к натуральным переменным начального симплекса.
Переход выполняется по формуле
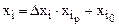, ( 4.16)
где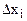 
– интервал варьирования в натуральных переменных; 
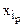– значение факторов в кодовых переменных; 
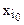– значение базы в натуральных переменных.
Пример. Координаты по оси x1 фактора a для вершины 1
x1 = 4×0,5 + 14 = 16,
для вершины 2
x1 = 4×(–0,5) + 14 = 12,
для вершин 3 и 4
x1 = 4×0 + 14 = 14.
Координаты остальных вершин исходного симплекса рассчитаны аналогично и сведены в табл. 4.2. Таблица 4.2
Координаты вершин исходного симплекса
| Симплекс | Вершина | Координата по оси | ||
| x1 | x2 | x3 | ||
| 16,7 | 0,56 | |||
| 16,7 | 0,56 | |||
| 11,5 | 0,56 | |||
| 0,32 |
8. Реализация плана первой серии экспериментов
Пример (табл.4.3).
Таблица 4.3
Результаты 1-й серии экспериментов
| Симплекс | Вершина | Выход (стойкость T, мин) |
| 37,3 | ||
| 31,5 | ||
| 32,5 | ||
| 40,0 |
9. Выбор наихудшего выхода
Пример: опыт 2 в табл. 7.3.
10. Проводится “отражение” наихудшей точки относительно центра противоположной грани. Координаты новой точки находятся по формуле
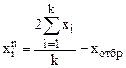, (4.17)
где n – порядковый номер вершины “нового” симплекса;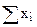 
– сумма факторов в натуральных переменных во всех вершинах симплекса кроме отброшенной; 
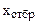– значение фактора в натуральных переменных в отброшенной вершине симплекса; i – порядковый номер фактора (i = 1, 2, 3 … k); k – число факторов (мерность факторного пространства).
Пример: координаты пятого эксперимента:
; 
;
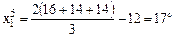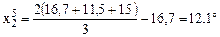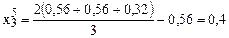мм.
11. Реализуем эксперимент во вновь построенной вершине симплекса.
Пример: (табл.4.4). Таблица 4.4
Результаты эксперимента в точке 5
| Но-мер опыта | Симп-лекс | Вер-шина | x1 | x2 | x3 | T |
| 17° | 12,1° | 0,4 мм | 40,7 мин |
Последовательное отбрасывание вершин симплекса и нахождение координат новых вершин (движение симплекса в факторном пространстве) продолжается, пока наблюдается рост критерия качества (выхода).
Примечания:
1) эксперименты прекращаются тогда, когда симплекс начинает вращаться вокруг точки оптимума или хотя бы одна из натуральных координат новой вершины симплекса не имеет физического смысла из-за своей величины.
Пример: табл.4.5. Таблица 4.5
Результаты экспериментов
| Но-мер опыта | Симп-лекс | Вер-шина | x1 | x2 | x3 | y |
| 17,3 | 17,7 | 0,29 | 47,2 | |||
| 16,5 | 13,2 | 0,12 | 47,8 | |||
| 19,9 | 13,7 | 0,22 | 50,6 | |||
| 18,8 | 17,6 | 0,02 | 67,0 | |||
| 19,5 | 12,0 | 0,01 | – |
В точке 10 (эксперимент №10) величина ленточки (f = 0,01 мм) слишком мала и не может быть рекомендована для производства;
2) при движении симплекса в факторном пространстве может встретиться частный оптимум, меньший истинного. Критериями для оценки оптимума являются априорные данные и опыт исследователя;
3) если после ”отражения” наихудшей точки симплекса получена новая точка, которая в новом симплексе также окажется наихудшей, то необходимо, вернувшись к прежнему симплексу, двигаться из него, отбросив точку, которая будет наихудшей, если не считать первой;
4) в некоторых случаях может оказаться, что процесс, который рассматривается как зависящий от i факторов, на самом деле зависит еще от какого-нибудь (i+1)-го фактора, величина которого в процессе проведения экспериментов не изменялась.
При этом можно “достроить” симплекс до (i+1)-мерного, вводя только одну новую точку. Для этого к точкам “старого” пространства с (i+1)-й координатой, равной d, надо присоединить еще одну точку, координаты которой
; 
… 
; 
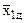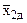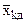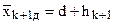. (4.18)
Здесь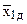 
– средние арифметические значения из соответствующих значений координат “предыдущего” симплекса в натуральных переменных, равные:
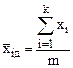, (4.19)
где k – мерность “старого” факторного пространства (число факторов); m – количество вершин “старого” симплекса; i – индекс номера фактора (i = 1, 2, 3 … k); д – индекс координат, добавочной точки “нового” симплекс.
Значение дополнительного (k + 1) фактора находится по формуле
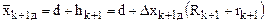, (4.20)
где d – величина (k + 1)-го фактора, которая в процессе проведения экспериментов по “старому” симплексу не учитывалась, но оставалась постоянной (в натуральных переменных);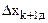 
– интервал варьирования (k + 1)-го фактора в натуральных переменных; 
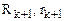– радиусы описанной и вписанной сфер симплекса размерностью k + 1.
Пример: при исследовании стойкости фрез не учитывалось влияние их твердости, равное 60 HRC (d = 60).
Принимаем: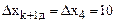 
(интервал варьирования),
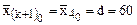(база).
Рассчитываем значения четырех факторов для 10-й точки “нового” симплекса 7, 9, 6, 8, 10.
; 
; 
;
.
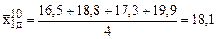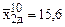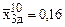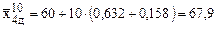После реализации этого эксперимента необходимо выявить наихудший выход и возобновить процесс “отражения” отброшенных вершин.
12. Повторить эксперимент в точке оптимума для устранения возможных ошибок и повышения достоверности данных.
Следует отметить, что симплекс-планы относятся к насыщенным (число опытов равно числу коэффициентов в уравнении регрессии). Это касается матрицы первого (исходного) симплекса и линейной регрессионной модели.
В матрице симплексного плана соблюдается условие ортогональности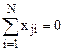 
и не соблюдается условие парной ортогональности 
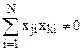и нормировки 
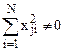. Эти планы ротатабельны. В подобных планах коэффициенты линейной модели определяются по формулам
; 
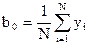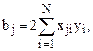( 4.21)
а их дисперсия
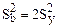. ( 4.22)
Следовательно, коэффициенты, найденные по симплекс-плану, определяются с меньшей точностью, чем по полнофакторному плану.
Адекватность полученной линейной модели может оцениваться только качественно по величине разности
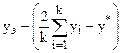, (7.23)
где уэ – экспериментальное значение выхода; yi – значение выхода в "хороших" вершинах симплекса; у* - наихудшее значение выхода (у отброшенной вершины); k – число факторов.
Чем больше эта величина (разность между экспериментальным и расчетным значениями выхода), тем менее верна гипотеза об адекватности линейной модели.
Таким образом методика симплексного планирования экспериментов может бать дополнена.
13. Расчет дисперсии воспроизводимости (табл.7.6)
Таблица 7.6
| № п/п | План | Выход | Примечание | |||||
| x1 | x2 | x3 |  |  |  |  | ||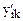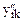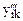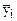
| 0,5 | 0,289 | 0,204 | 37,1 | 36,7 | 38,1 | 37,3 | Выполнено только три параллельных опыта в вершине симплекса №1 | |
| –0,5 | 0,289 | 0,204 | – | – | – | 31,5 | ||
| –0,578 | 0,204 | – | – | – | 32,1 | |||
| –0,612 | – | – | – | 40,0 |
.
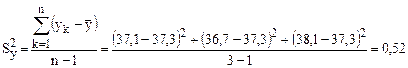14. Расчет коэффициентов уравнения регрессии (табл.7.7).
Таблица 7.7
| № п/п | План | Выход | Расчет | ||||
| x1 | x2 | x3 | yi | x1yi | x2yi | x3yi | |
| 0,5 | 0,289 | 0,204 | 37,3 | 18,65 | 10,7797 | 7,6092 | |
| –0,5 | 0,289 | 0,204 | 31,5 | –15,75 | 9,1035 | 6,426 | |
| –0,578 | 0,204 | 32,1 | –18,5538 | 6,5484 | |||
| –0,612 | 40,0 | –24,48 | |||||
| S | 140,9 | 2,9 | 1,3294 | –3,8964 |
.
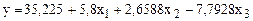15. Расчет значимости коэффициентов регрессии (табл.4.8).
Таблица 4.8
| № п/п | Коэффициенты | Критерий Стьюдента | Вывод | |
| расчетный | табличный | |||
| 35,225 | 34,5 > | 4,303 | ||
| 5,8 | 5,69 > | |||
| 2,6588 | 2,607 < | Незначим | ||
| 7,7928 | 7,64 > |
; 
.
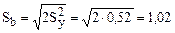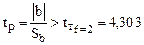16. Оценка адекватности линейной модели
.
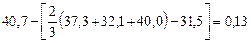Принимаем гипотезу о линейной модели. Таким образом, итогом проведения симплекс–планирования является знание оптимального значения параметра выхода и величин переменных факторов, обеспечивающих этот оптимум.