Дележи при затруднительных обстоятельствах

Есть известная восточная притча о том, что отец оставил сыновьям 17 верблюдов и велел разделить между собой: старшему половину, среднему - треть, младшему- девятую часть. Но 17 не делится ни на 2, ни на 3, ни на 9. Сыновья обратились к мудрецу. Мудрец был знаком с дробями и смог помочь в этой затруднительной ситуации.

Он пустился на уловку. Мудрец прибавил к стаду на время своего верблюда, тогда их стало 18. Разделив это число, как сказано в завещании, мудрец забрал своего верблюда обратно. Секрет в том, что части, на которые по завещанию должны были делить стадо сыновья, в сумме не составляют 1. Действительно, 1\2 + 1\3 + 1\9 = 17\18.

Таких задач достаточно много. Например, задача из русского учебника о 4 друзьях, нашедших кошелек с 8 кредитными билетами: по одному в один, три, пять рублей, а остальные десятирублевые. По обоюдному согласию один хотел третью часть, второй-четверть, третий- пятую, четвертый-шестую. Однако самостоятельно они этого сделать не смогли: помог прохожий, предварительно добавив свой рубль. Чтобы разрешить эту трудность прохожий сложил единичные дроби 1\3 + 1\4 + 1\5 + 1\6 = 57\60, удовлетворив запросы друзей и заработав 2 рубля для себя. [3]

III. Занимательные дроби

Дроби-домино

Домино – настольная игра, распространенная во всем мире. Игра домино чаще всего состоит из 28 прямоугольных плиток-костей. Костяшка домино представляет собой прямоугольную плитку, лицевая сторона которой разделена линией на две квадратные части. Каждая часть содержит от нуля до шести точек. Если убрать кости, не содержащие очков хотя бы на одной половине (бланши), то оставшиеся кости можно рассматривать как дроби. Кости, обе половины которых содержат по одинаковому количеству очков (дубли), представляют из себя неправильные дроби, равные единице. Если убрать еще эти кости, то останется 15 костей. Их можно располагать по-разному и получать интересные результаты. [4]

1. Расположение в 3 ряда, сумма дробей в каждом из которых, равна 2 .

; ;

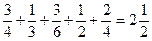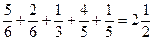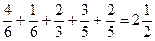
2. Расположение всех 15 костей в три ряда по 5 костей в каждом, употребляя некоторые из костей домино как неправильные дроби, например 4/3, 6/1, 3/2 и т. д., так, чтобы сумма дробей в каждом ряду равнялась числу 10.

1\3+6\1+3\4+5\3+5\4=10

2\1+5\1+2\6+6\3+4\6=10

4\1+2\3+4\2+5\2+5\6=10

3. Расположение в ряды дробей, сумма которых будет числом целым (но разным в разных рядах).

Из глубины веков.

«Он скрупулёзно изучил этот вопрос». Это означает, что вопрос изучен до конца, что не одной самой малой неясности не осталось. А происходит странное слово «скрупулёзно» от римского названия 1/288 асса – «скрупулус».

«Попасть в дроби». Это выражение означает попасть в трудное положение.

«Асс» - единица измерения массы в фармакологии (аптекарский фунт).

«Унция» - единица массы в английской системе мер, единица измерения массы в фармакологии и химии.

IV. Заключение.

Учение о дробях считалось самым трудным разделом математики во все времена и у всех народов. Кто знал дроби, был в почете. Автор старинной славянской рукописи XVв. пишет: «Несть се дивно, что …в целых, но есть похвально, что в долях…».

Я сделала вывод, что история обыкновенных дробей - это извилистая дорога со многими препятствиями и трудностями. При работе над рефератом я узнала много нового и интересного. Прочитала много книг и разделов из энциклопедий. Познакомилась с первыми дробями, которыми оперировали люди, с понятием аликвотная дробь, узнала новые для меня имена ученых, внесших свой вклад в развитие учения о дробях. Сама попробовала решать олимпиадные и занимательные задачи, самостоятельно подбирала примеры разложения обыкновенных дробей на аликвотные дроби, разбирала решение приведенных в текстах примеров и задач. Ответ на вопрос, который я задала себе перед началом работы над рефератом: обыкновенные дроби необходимы, они важны. Интересно было готовить презентацию, пришлось обращаться за помощью к учителю и одноклассникам. Так же при наборе текста я впервые столкнулась с необходимостью печатать дроби и дробные выражения. На школьной конференции я представила свой реферат. Так же выступала перед своими одноклассниками. Слушали очень внимательно и, по-моему, им было интересно.

Задачи, которые я ставила перед началом работы над рефератом, считаю, мною выполнены.

Литература.

1.Бородин А.И. Из истории арифметики. Головное издательство «Вища школа»-К.,1986

2. Глейзер Г. И. История математики в школе: IV-VI кл. Пособие для учителей. – М.: Просвещение, 1981.

3.Игнатьев Е.И. В царстве смекалки. Главная редакция физико-математической литературы издательства «Наука»,М.,1978.

4. Кордемской Г.А.Математическая смекалка.-10-е изд., перераб. И доп.-М.:Юнисам,МДС,1994.

5.Стройк Д.Я. Краткий очерк истории математики. М.: Наука, 1990.

6.Энциклопедия для детей. Том 11. Математика. Москва, «Аванта+»,1998.

7. http://ru.wikipedia.org/wiki.Материал из Википедии — свободной энциклопедии.

Приложение 1.

Природный звукоряд

Все знают, что Пифагор был учёным и, в частности, автором знаменитой теоремы. А то, что он был еще и блестящим музыкантом, известно не так широко. Сочетание этих дарований позволило ему первым догадаться о существовании природного звукоряда. Надо было ещё доказать это. Пифагор построил для своих экспериментов полуинструмент-полуприбор — «монохорд». Это был продолговатый ящик с натянутой поверх него струной. Под струной, на верхней крышке ящика, Пифагор расчертил шкалу, чтобы удобнее было зрительно делить струну на части. Множество опытов проделал Пифагор с монохордом и, в конце концов, описал математически поведение звучащей струны. Работы Пифагора легли в основу науки, которую мы называем сейчас музыкальной акустикой. Оказывается, для музыки семь звуков внутри октавы такая же естественная вещь, как десять пальцев на руках в арифметике. Уже тетива самого первого лука, колеблясь после выстрела, давала готовым тот набор музыкальных звуков, которыми мы почти без изменения пользуемся до сих пор.

С точки зрения физики тетива и струна — одно и то же. Да и сделал человек струну, обратив внимание на свойства тетивы. Звучащая струна колеблется не только целиком, но одновременно и половинками, третями, четвертями и т.д. Подойдём теперь к этому явлению с арифметической стороны. Половинки колеблются вдвое чаще, чем целая струна, трети — втрое, четверти — вчетверо. Словом, во сколько раз меньше колеблющаяся часть струны, во столько же раз больше частота её колебаний. Допустим, вся струна колеблется с частотой 24 герца. Высчитывая колебания долей вплоть до шестнадцатых, мы получим ряд чисел, показанных в таблице. Эта последовательность частот так и называется — натуральный, т.е. природный, звукоряд.

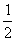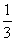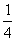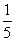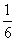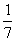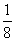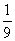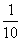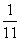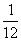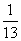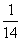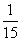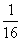Приложение 2.