Расчет параметров уравнения множественной регрессии

Параметры множественной регрессии, как и параметры парной регрессии можно определить, используя МНК. Так для расчета параметров уравнения множественной линейной регрессии:

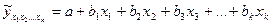
МНК даст систему уравнений:

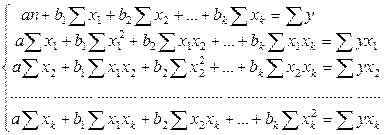(9.123)

Параметры уравнения находим как отношение частных определителей к определителю системы

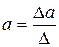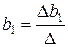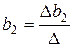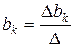, , ,…, (9.124)

где

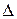- определитель системы, находится, как:

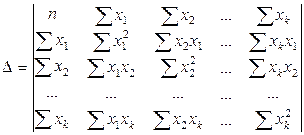(9.125)

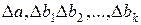- частные определители системы рассчитывают, заменяя соответствующий столбец матрицы определителя системы данными левой части системы.

Параметр 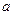во множественной регрессии называется свободным членом уравнения регрессии и также как в парной регрессии не имеет экономической интерпретации. Параметр 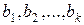- коэффициентом регрессии, он показывает, на сколько единиц, в среднем, изменится результативный признак 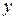, если соответствующий данному коэффициенту фактор 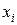увеличится на одну единицу при постоянной величине остальных факторов.

Коэффициенты регрессии можно рассчитать и используя уравнения регрессии в стандартизованном виде представив все переменные уравнения как центрированные и нормированные. Для этого выразим их как отношение их отклонений от средних величин на их стандартное отклонение:

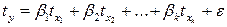(9.126)

где

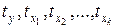- стандартизованные переменные:

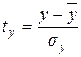(9.127)

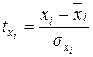(9.128)

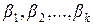- стандартизованные коэффициенты регрессии 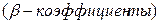, показывают на сколько, в среднем, среднеквадратических отклонений изменится вариация результативного признака 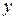, если вариация соответствующего фактора 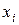увеличится на одно среднеквадратическое отклонение, при постоянной величине остальных факторов. Расчет параметров уравнения в стандартизированной форме более прост, так как, по сравнению с уравнением в натуральной форме отсутствует параметр .

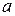МНК для уравнения множественной регрессии в стандартизированном масштабе даст следующую систему уравнений:

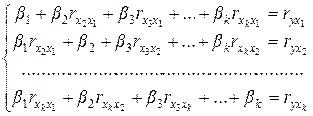(9.129)

где

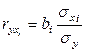- коэффициент парной корреляции (9.130)

или 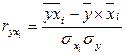(9.131)

Как, и в уравнении в натуральном масштабе параметры стандартизированного уравнения можно найти методом определителей:

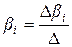(9.132)

где:

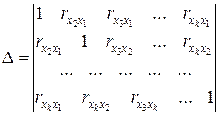(9.133)

Определитель 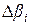получается из определителя 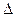, заменой в нем соответствующего столбца столбцом свободных членов исходной системы.

Кроме того, 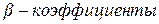можно рассчитать используя их взаимосвязь с коэффициентами парной линейной корреляции. Так, например, 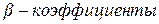для двухфакторной линейной модели, выраженной в стандартизованном масштабе, 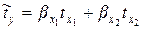рассчитываются, как:

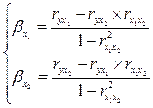(9.134)

Определив значение b-коэффициентов и зная, что между b-коэффициентами и коэффициентами регрессии в натуральном масштабе 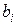существует следующая взаимосвязь:

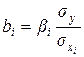или 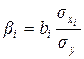(9.135)

От уравнения множественной регрессии в стандартизованном виде

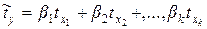(9.136)

перейдем к уравнению в натуральном масштабе

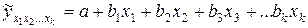(9.137)

параметр 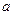, который не рассчитали в стандартизованном уравнении, рассчитаем, как

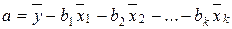(9.138)

Расчет параметров нелинейных уравнений множественной регрессии ведется так же, как и в линейной модели используя МНК. Разница заключается в том, что нелинейные модели вначале линеаризуются, и расчет параметров проводится по преобразованным данным (см. парную регрессию).

Частные уравнения регрессии

Частные уравнения регрессии, рассчитываются на основе множественного уравнения регрессии:

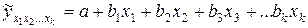(9.139)

Они показывают изолированное влияние одного конкретного 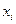фактора на результативный признак 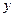, при зафиксированном, на среднем уровне, положении остальных, включенных в модель факторов. Влияния зафиксированных факторов в уравнениях частной регрессии присоединены к свободному члену уравнения регрессии .

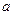Частные множественные регрессии записываются, как:

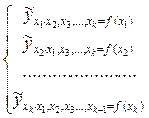(9.140)

Обозначение 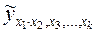показывает, что изучается влияние на результат 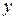, фактора 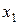, при зафиксированном на среднем уровне положении факторов 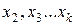. Обозначение 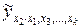показывает, что изучается влияние на результат 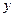, фактора 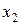, при зафиксированном на среднем уровне положении факторов 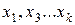, и т, д. Знак 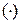в нижнем индексе обозначения отделяет фактор влияния, которого исследуется, от факторов, влияние которых изолируется.

Частные уравнения множественной регрессии для линейной модели имеют вид:

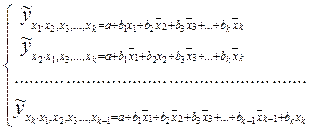(9.141)

На основе частных уравнений регрессии рассчитывают частные коэффициенты эластичности:

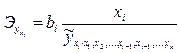(9.142)

Частные коэффициенты эластичности отличаются от средних коэффициентов.

Частный коэффициент эластичности показывает, на сколько, в среднем, процентов изменится результат при подстановке в уравнение регрессии конкретного значения .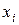

Средний коэффициент эластичности 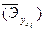показывает, на сколько в среднем процентов изменится результат, если соответствующий данному коэффициенту фактор увеличится на 1%, при зафиксированных, на средних уровнях величин остальных, включенных в модель, факторов.

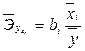(9.143)

1.9.4.6.3 Множественная корреляция

Силу связи во множественных моделях изучают с помощью показателя множественной корреляции и его квадрата – показателя множественной детерминации.

Показатель множественной корреляции 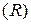– показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Может принимать значения от 0 до 1, то есть в отличие от парной модели не показывает направление связи.

Показатель множественной детерминации 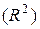- показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов.

В статистике и эконометрике показатель множественной корреляции (детерминации) принято называть индексом или коэффициентом множественной (совокупной) корреляции.

Для линейной множественной функции и для функций нелинейных по переменным (полиномы разных степеней, равносторонняя гипербола и т.п. функции) индекс множественной корреляции совпадает скоэффициентом множественной корреляции.

Коэффициент (индекс) множественной корреляции рассчитывают, используя следующие формулы:

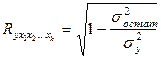(9.144)

где:

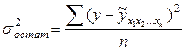- остаточная дисперсия (9.145)

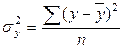- общая дисперсия для признака 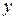(9.146)

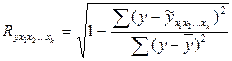(9.147)

Коэффициент множественной корреляции можно рассчитать и, как:

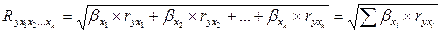(9.148)

где:

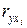- парные коэффициенты корреляции между результативным признаком 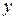и одним из факторов .

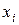Для функций нелинейных по оцениваемым параметрам (степенная, показательная, экспоненциальная и т. п. функции) индекс множественной корреляции не совпадает скоэффициентом множественной корреляции. Его называют « 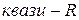» и определяют как

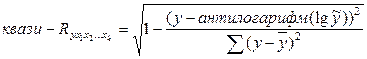(9.149)

Коэффициенты (индексы) множественной детерминации получают, возводя коэффициенты (индексы) корреляции в квадрат, или по формулам.

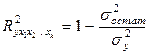(9.150)

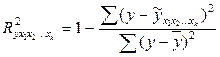(9.151)

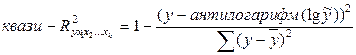(9.152)