Линеаризация степенной функции

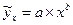(9.62)

проводят путем логарифмирования обеих частей уравнения, получая уравнение вида:

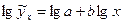(9.63)

Обозначив через 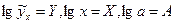, получим линейное уравнение регрессии:

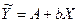(9.64)

МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:

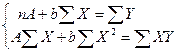(9.65)

Также можно использовать уравнения:

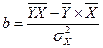(9.66)

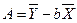(9.67)

Рассчитав параметры 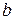, 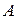и составив линейное уравнение регрессии необходимо провести его потенцирование, чтобы вернуться к степенной функции.

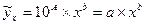(9.68)

Линеаризация показательной функции

Показательная функция

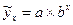(9.69)

также проводят путем логарифмирования обеих частей уравнения:

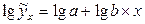(9.70)

Обозначив через 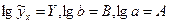, получим линейное уравнение регрессии:

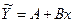(9.71)

МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:

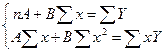(9.72)

Также можно использовать уравнения:

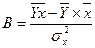(9.73)

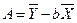(9.74)

Рассчитав параметры 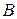, 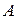и составив линейное уравнение регрессии необходимо провести его потенцирование, что бы вернуться к показательной функции.

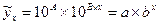(9.75)

1.9.4.2.1 Коэффициенты эластичности в парных моделях

Коэффициенты регрессии 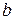выражены в натуральных единицах, то есть являются именованными величинами, поэтому коэффициенты регрессии, выраженные в разных единицах несопоставимы между собой. Для сопоставления разноименных коэффициентов корреляции линейных и нелинейных моделей удобно использовать коэффициент эластичности.

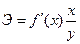(9.76)

где:

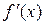- первая производная функции регрессии для соответствующей формы связи.

Так как коэффициент эластичности не всегда величина постоянная, а часто зависит от значения 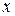, обычно рассчитывают средний коэффициент эластичности.

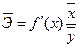(9.77)

Коэффициент средней эластичности для некоторых функций рассчитывается как:

· уравнение прямой :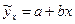

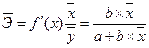(9.78)

· парабола второго порядка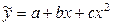

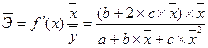
· уравнение равносторонней гиперболы :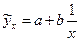

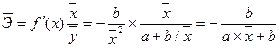(9.79)

· степенного уравнения :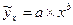

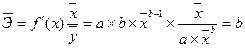(9.80)

· показательного уравнения :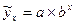

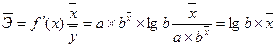(9.81)

Коэффициент средней эластичности показывает, на сколько процентов в среднем изменится результативный признак, если факторный признак увеличится на один процент.

Коэффициент средней эластичности позволяет ранжировать факторы по силе влияния на результат, чем больше коэффициент для 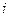-го фактора, тем сильнее данный фактор влияет на результат.

1.9.4.3 Парная нелинейная корреляция

В нелинейных моделях для определения силы связи рассчитывают индекс корреляции:

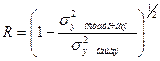(9.82)

где;

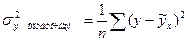- остаточная дисперсия результативного признака.

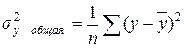- общая дисперсия результативного признака.

Отсюда: 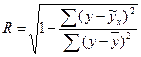(9.83)

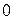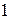Величина индекса корреляции может принимать значения от до , то есть, он показывает только тесноту связи, но не показывает ее направление.

Квадрат индекса корреляции – индекс детерминации характеризует долю вариации результативного 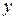признака обусловленную влиянием включенного в модель фактора .

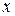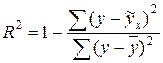(9.84)

Величина индекса детерминации определяет качество подбора функции регрессии, чем индекс детерминации выше, тем «лучше» выбор формы уравнения регрессии.

1.9.4.4 Оценка статистической надежности в парных нелинейных моделях

Как и в парной линейной регрессии, в регрессии нелинейной оценку надежности уравнения в целом проводят с помощью критерия Фишера (F-критерия), а оценку параметров уравнения и коэффициента детерминации проводят с помощью критерия Стьюдента.

Общая формула фактического F-критерия имеет вид;

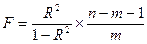(9.85)

где:

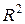- индекс детерминации.

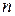- число наблюдений.

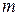- число параметров при переменных .

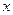В случае нелинейной регрессии 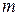отлично для разных видов регрессии, и формула F-критерия различна для различных функций.

Например. Для степенной 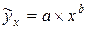и показательно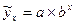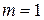й и:

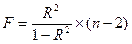(9.86)

Для параболы второго порядка 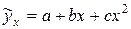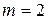и:

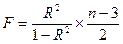(9.87)

Для параболы третьего порядка 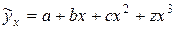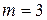и:

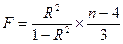(9.88)

Как и в случае линейной регрессии, критерий Фишера фактический сравнивают с критерием Фишера табличным, при определенном уровне значимост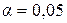и или 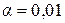, и числе степеней свободы - 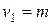, 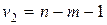(таблицы Снедекора-Фишера – приложение 2).

Значимость параметров уравнения парной нелинейной регрессии и индекса корреляции проверяется, аналогично парной линейной регрессии, используя критерий Стьюдента.

Критерий Стьюдента для коэффициента регрессии 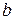рассчитывается как;

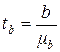(9.89)

где; 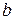- коэффициент регрессии.

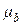- стандартная ошибка коэффициента регрессии, рассчитывается как:

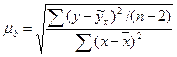(9.90)

Учитывая, что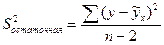

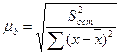(9.91)

Критерий Стьюдента для параметра 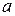рассчитывается как;

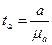(9.92)

где: 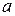- свободный член уравнения регрессии.

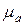- стандартная ошибка параметра 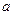, рассчитывается как:

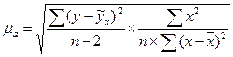(9.93)

или 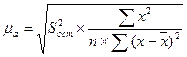(9.94)

Критерий Стьюдента для индекса корреляции 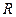рассчитывается как;

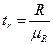(9.95)

или 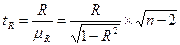(9.96)

где: 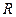- индекс корреляции.

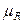- стандартная ошибка индекса корреляции, рассчитывается как:

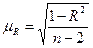(9.97)

Качество подбора модели 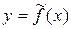определяют, рассчитывая среднюю ошибку аппроксимации. Для расчета средней ошибки аппроксимации используют формулы:

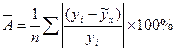(9.98)

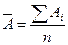(9.99)

где 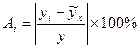(9.100)

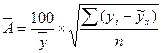(9.101)

Чем меньше средняя ошибка аппроксимации, тем выше качество модели. Допустимый предел 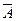не более 10%.

1.9.4.5 Прогнозирование на основе парной модели регрессии. Расчет доверительных интервалов

Парные модели регрессии 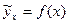позволяют прогнозировать значение результативного признака 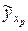как точечный прогноз 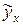путем подстановки в уравнение регрессии соответствующего конкретного прогнозного значения .

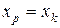Естественно, что полученное точечное значение 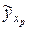рассчитанное для 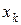не может быть на 100% точным, поэтому необходим дополнительный расчет стандартной ошибки для функции регрессии и для индивидуальных значений зависимой переменной, и построение соответствующих интервалов 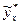которые с заданной вероятностью 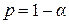( 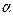- уровень значимости) накрывают неизвестное значение 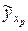. Также доверительные интервалы рассчитываются для параметров уравнения регрессии 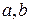и коэффициента (индекса) корреляции .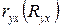