Для нахождения неизвестных параметров применяем Метод максимального правдоподобия

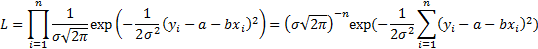
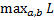достигается при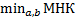

Оценки по методу ММП для параметров a и b являются также оценками по методу МНК.

( , )

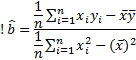
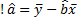
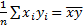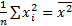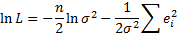
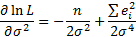
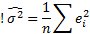
Практика в R:

alcohol = data.frame(x = c(46.2, 43.4, 37.8, 39.2, 42.0, 44.8), y = c(33, 31, 27, 28, 30, 32));

(alcohol.lm = lm(y ~ x - 1, alcohol))

Call:

lm(formula = y ~ x - 1, data = alcohol)

Coefficients:

x

0.7143

plot(alcohol$x, alcohol$y)

abline(alcohol.lm, col="blue")

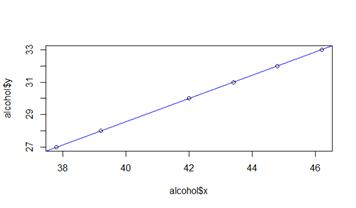
summary(alcohol.lm)

Call:

lm(formula = y ~ x - 1, data = alcohol)

Residuals:

1 2 3 4 5 6

E-14 -6.228e-16 2.552e-15 -4.459e-15 -4.270e-15 -4.081e-15

Coefficients:

Estimate Std. Error t value Pr(>|t|)

x 7.143e-01 5.524e-17 1.293e+16 <2e-16 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.729e-15 on 5 degrees of freedom

Multiple R-squared: 1, Adjusted R-squared: 1

F-statistic: 1.672e+32 on 1 and 5 DF, p-value: < 2.2e-16

Модель Гаусса – Маркова простой линейной регрессии. Проверка значимости регрессии, изменение модели и прогноз новых значений в пакете R.

Теория:

Проверка значимости

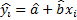
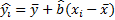
Мера разброса y относительно -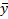

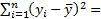
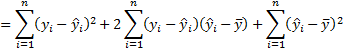
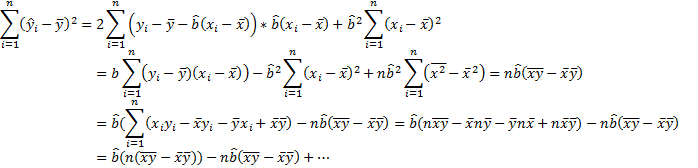
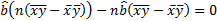
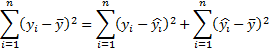
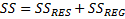
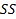-полная сумма квадратов

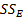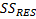или – отклонение наблюдения от прогноза

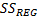– объяснённая регрессией сумм квадратов

Дисперсионное разложение – качество подгонки модели

Если модель корректна, то .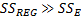

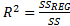– коэффициент детерминации (обусловленности)

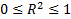
Показывает, насколько хорошо объясняется зависимая переменная. Чем 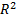ближе к 1, тем лучше.

Предположение о нормальности параметров

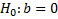(функциональная независимость) модель незначима

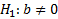модель значима

Пр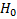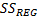и :

и 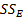- независимы

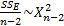, , n- число наблюдений

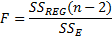
Область отвержения 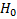– область значений F, превышающих критичное табличное значение.

Практика в R:

cost = data.frame(x = c(1, 2, 3, 5, 10, 20, 30, 50, 100, 200), y = c(10.15, 5.52, 4.08, 2.85, 2.11, 1.62, 1.41, 1.30, 1.21, 1.15)); # кадр данных

#Подобрать логарифмическую модель y=a+b/x

(cost.lm = lm(y ~ I(1 / x), cost))

plot(1 / cost$x, cost$y)

abline(cost.lm, col="blue")

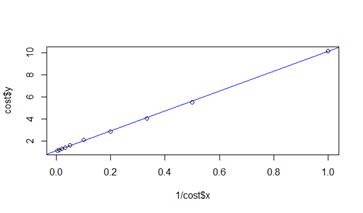
plot(cost$x, cost$y)

ab = cost.lm$coefficients;

with(cost, lines(x, ab[1] + ab[2] / x, col="blue"))

lines (cost$x, cost.lm$fitted.values) # or

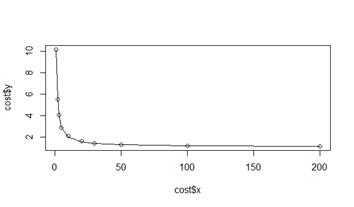
summary(cost.lm) # отчёт

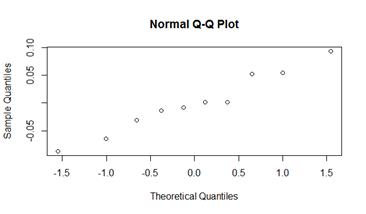
qqnorm(cost.lm$residuals) # Normal test for residuals

shapiro.test(cost.lm$residuals) # -=-

Модель линейной множественной регрессии. Ее применение для выявления нелинейных зависимостей для одной и нескольких переменных. Работа с этими моделями в пакете R.

Теория:

Практика в R:

Пример N1:

# Galileo Galilei

gal = data.frame(d = c(100, 200, 300, 450, 600, 800, 1000), h = c(253, 337, 395, 451, 495, 531, 574))

(gal.lm = lm (d ~ h + I(h ^ 2), gal))

lm(formula = d ~ h + I(h^2), data = gal)

Coefficients:

(Intercept) h I(h^2)

587.320391 -3.942494 0.008115

plot (gal$h, gal$d)

lines (gal$h, gal.lm$fitted.values)

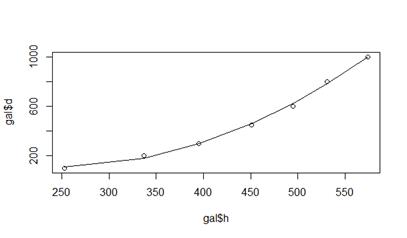
summary(gal.lm)

Call:

lm(formula = d ~ h + I(h^2), data = gal)

Residuals:

1 2 3 4 5 6 7

-9.311 19.672 3.800 -9.883 -24.198 17.992 1.928

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 5.873e+02 1.220e+02 4.813 0.008564 **

h -3.942e+00 6.134e-01 -6.428 0.003012 **

I(h^2) 8.115e-03 7.351e-04 11.040 0.000383 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 19.36 on 4 degrees of freedom

Multiple R-squared: 0.9977, Adjusted R-squared: 0.9965

F-statistic: 854.9 on 2 and 4 DF, p-value: 5.447e-06

shapiro.test(gal.lm$residuals)

Shapiro-Wilk normality test

data: gal.lm$residuals

W = 0.94492, p-value = 0.6834

(gal.lm3 = update(gal.lm, . ~ . + I(h ^ 3)))

Call:

lm(formula = d ~ h + I(h^2) + I(h^3), data = gal)

Coefficients:

(Intercept) h I(h^2) I(h^3)

-6.902e+01 1.260e+00 -4.983e-03 1.056e-05

plot (gal$h, gal$d)

lines (gal$h, gal.lm3$fitted.values)

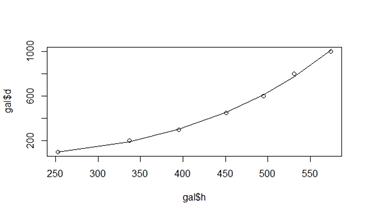
summary(gal.lm3)

Call:

lm(formula = d ~ h + I(h^2) + I(h^3), data = gal)

Residuals:

1 2 3 4 5 6 7

-1.808 6.237 -1.846 -4.108 -14.097 24.453 -8.832

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -6.902e+01 5.020e+02 -0.137 0.899

h 1.260e+00 3.921e+00 0.321 0.769

I(h^2) -4.983e-03 9.792e-03 -0.509 0.646

I(h^3) 1.055e-05 7.872e-06 1.341 0.272

Residual standard error: 17.67 on 3 degrees of freedom

Multiple R-squared: 0.9985, Adjusted R-squared: 0.9971