Гидравлические сопротивления в трубопроводах и каналах
Расчет гидравлического сопротивления при движении реальных жидкостей в трубопроводах и каналах является одной из основных прикладных задач гидродинамики (внутренняя задача). Это связано с необходимостью расчета затрат энергии, требуемых для компенсации потерь напора (давления) и перемещения жидкостей (газов) насосами или компрессорами.
Потери напора в каналах обусловлены сопротивлением трения и местными сопротивлениями в потоке жидкости.
Сопротивление трения имеет место по всей длине трубопровода. На его величину оказывает влияние режим течения жидкости.
Местные сопротивления появляются при любых изменениях скорости потока по величине и (или) направлению. К местным сопротивлениям относят вход в канал и выход потока из канала, внезапные сужения и расширения труб, отводы, колена, тройники, запорные и регулирующие устройства (рис. 2.16, 2.17).
      |
Таким образом, потерянный напор представляет сумму двух слагаемых
.
Потери напора на трение по длине трубопровода равны:
.
Коэффициент трения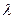 
зависит от режима течения и относительной шероховатости стенок канала 
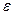. Для гладких стенок трубопроводов 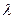определяется в зависимости от числа Рейнольдса по следующим формулам:
для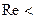 
2300 
;
для 400 
105 
.
При расчете коэффициента трения для всех областей турбулентного течения с учетом шероховатости стенок каналов применимо обобщенное уравнение
,
если шероховатостью стенок можно пренебречь, то уравнение для расчета коэффициента трения имеет вид
.
    |
Потери напора на преодоление местных сопротивлений оценивается в долях скоростного напора по формуле Вейсбаха
.
Значения коэффициентов местных сопротивлений 
находятся опытным путем и приведены в справочной литературе.
Движение тел в жидкостях
Проведение ряда процессов связано с движением твердых тел в капельных жидкостях или газах. Движение тел в жидкостях имеет место в процессах осаждения твердых частиц из суспензий, пылей под действием гравитационных и центробежных сил, механического перемешивания в жидких средах и др.
Если частица массой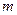 
падает под действием силы тяжести, то ее скорость движения со временем должна возрастать (рис. 2.18).
 |
При отсутствии сопротивления среды скорость частицы определялась бы по известному уравнению
.
Однако с увеличением скорости растет и сопротивление, определяемое по уравнению
,
где 
- коэффициент сопротивления.
С ростом сопротивления движению частицы будет уменьшаться ее ускорение. В результате этого через определенное время установится динамическое равновесие: сила тяжести, под действием которой частица движется, станет равной силе сопротивления среды. С этого момента времени частица начнет двигаться равномерно – с постоянной скоростью 
. Эта скорость называется скоростью осаждения.
Сила, движущая шарообразную частицу диаметром 
и плотностью 
в процессе осаждения, определяется разностью между силой тяжести и выталкивающей Архимедовой силой, равной весу жидкости в объеме частицы:
.
Скорость осаждения можно вычислить из условия равенства сил, обеспечивающих движение, и силы сопротивления:
,
откуда
. (2.6)
Значение коэффициента сопротивления в зависимости от режима осаждения можно определить по следующим зависимостям:
для ламинарного режима ( 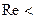2)
;
для переходного режима (2 500)
;
для турбулентного режима ( 
500)
0,44.
При подстановке в уравнение (2.6) зависимости для коэффициента сопротивления для ламинарного режима получим уравнение, называемое уравнением Стокса для процесса осаждения:
. (2.7)
Используя это уравнение, можно найти максимальный размер частиц, осаждение которых происходит по закону Стокса. Для этого в уравнение (2.7) вместо скорости осаждения необходимо подставить ее выражение через критерий Рейнольдса 
. Принять критерий 
2, соответствующий предельному значению для ламинарного режима течения, и получить
.
Существует и нижний предел применимости закона Стокса, соответствующий 
10-4. При 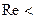10-4 на скорость осаждения очень мелких частиц начинает влиять тепловое (броуновское) движение молекул среды.
Уравнение (2.6) в связи с тем, что зависит от скорости осаждения, необходимо решать методами последовательных приближений.
Вследствие трудоемкости метода последовательных приближений удобнее всего для определения пользоваться методом, предложенным П.В. Лященко. Этот метод основан на преобразовании уравнения (2.6) путем подстановки в него скорости осаждения, выраженной через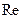 
, и возведения обеих частей уравнения во вторую степень:
,
откуда
.
Выражение в правой части этого уравнения представляет собой критерий Архимеда
.
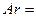
В критерий Архимеда искомая скорость осаждения не входит. Он содержит величины, которые обычно либо заданы, либо могут быть заранее определены.
Таким образом
.
Подставив в это обобщенное уравнение граничные значения критерия Рейнольдса, соответствующие переходам из одной области осаждения в другую, можно найти соответствующие им критические значения критерия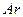 
.
Для 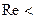2 за счет подстановки выражения для 
получим
,
откуда
.
Критическое значение критерия Архимеда для ламинарной области -
.
Следовательно, существование ламинарного режима осаждения соответствует условию 
.
Для переходной зоны 
после подстановки значения для получим
или
.
При подстановке в это уравнение критического значения 
можно найти верхнее предельное значение для переходной области
,
откуда
.
Таким образом, переходная область осаждения соответствует
36 
83000.
Для автомодельной области, где 
83000, зависимость между критериями можно найти, подставив 0,44:
.
Таким образом, рассчитав критерий 
, можно определить и установить область, в которой происходит осаждение. Затем по уравнению, характерному для данного режима осаждения, рассчитывают критерий Рейнольдса. И затем по критерию Рейнольдса вычисляют скорость осаждения:
.
Для всех режимов осаждения скорость процесса может быть рассчитана по критерию Рейнольдса на основании единой интерполяционной зависимости:
.
Скорость осаждения частиц не шарообразной формы меньше, чем скорость осаждения шарообразных частиц. Для вычисления скорости нешарообразных частиц используется коэффициент формы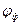 
:
.
Коэффициент формы 
1 определяется опытным путем. Для частиц округлой формы 
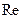0,77, угловатых - 0,66, продолговатых - 0,58, пластинчатых частиц - 0,43. При расчете критериев подобия и 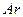для частиц не шарообразной формы в качестве определяющего размера используется эквивалентный диаметр
.
Расчет скорости осаждения капель жидкости в газе или в другой жидкости и пузырьков газа в жидкости даже для одиночных капель и пузырей усложняется вследствие изменения формы при их движении.