Это уравнение можно записать для расчета плотности газа

.

В ряде задач необходимо учитывать также состояние жидкостей. Для изоэнтропийных процессов в жидкости можно применять уравнение Тета

,

где - давление молекулярного взаимодействия; n - постоянный коэффициент, зависящий от свойств жидкостей. Для воды »3,2×10⁸ Па,
n » 7,15.

В зависимости от температуры и давления вещество может находиться в трех агрегатных состояниях: твердом, жидком и газообразном. В твердых телах молекулы взаимосвязаны между собой, расположены в определенном порядке и совершают только тепловое колебательное движение. Вероятность покинуть занимаемое молекулой (атомом) место мала. Поэтому твердые тела сохраняют заданную форму и объем.

В жидкостях тепловое движение молекул существенно выше, часть молекул получает достаточную энергию возбуждения и покидает свои места. Поэтому в жидкости молекулы перемещаются по всему объему, но их кинетическая энергия остается недостаточной для выхода за пределы жидкости. В этой связи жидкости сохраняют свой объем.

В газах тепловое движение еще больше, молекулы удалены настолько, что взаимодействие между ними становится недостаточным для удержания на определенном удалении, т.е. газ имеет возможность беспредельно расширяться.

Свободное перемешивание молекул в жидкостях и газах приводит к тому, что они изменяют свою форму при приложении сколь угодно малого силового действия. Это явление называют текучестью. Жидкости и газы принимают форму того сосуда, в котором они содержатся.

В результате хаотического движения молекулы в газе претерпевают столкновения. Процесс столкновения молекул характеризуется эффективным диаметром молекул, под которым понимается минимальное расстояние между центрами молекул при их сближении. Расстояние, которое молекула проходит между столкновениями, называется свободным пробегом молекулы.

В результате переноса количества движения при переходе молекул, движущихся с разными скоростями, из слоя в слой возникает касательная сила между слоями. Свойство жидкости и газа сопротивляться сдвигающим усилиям называют вязкостью.

Расположим в жидкой среде пластину 1 на некотором расстоянии от стенки (рис. 2.1).

Пусть пластина движется относительно стенки 2 со скоростью w. Так как жидкость будет увлекаться пластиной, то в зазоре установится послойное течение жидкости со скоростями, изменяющимися от 0 до w . Выделим в жидкости слой толщиной dy. Очевидно, что скорости нижней и верхней поверхности слоя будут отличаться по толщине на dw. В результате теплового движения молекулы непрерывно переходят из нижнего слоя в верхний и обратно. Так как их скорости различны, то их количества движения тоже различны. Но, переходя из слоя в слой, они должны принимать количество движения, характерное данному слою, т.е. будет иметь место непрерывное изменение количества движения, от чего появится касательная сила между слоями.

Обозначим через dT касательную силу, действующую на поверхность слоя площадью dF, тогда

.

Опыт показывает, что касательная сила Т, которую надо приложить для сдвига, тем больше, чем больше градиент скорости , характеризующий изменение скорости, приходящейся на единицу расстояния по нормали между слоями. Кроме того, сила Т пропорциональна площади соприкосновения F слоев, т.е.

.

В такой форме уравнение выражает закон внутреннего трения Ньютона, согласно которому напряжение внутреннего трения, возникающее между слоями жидкости при ее течении, прямо пропорционально градиенту скорости.

Знак минус в правой части уравнения указывает на то, что касательное напряжение тормозит слой, движущийся с относительно большой скоростью.

Коэффициент пропорциональности 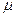в приведенных уравнениях называется динамическим коэффициентом вязкости.

Размерность динамического коэффициента вязкости в СИ может быть выражена как

.

Вязкость жидкостей также можно характеризовать кинематическим коэффициентом вязкости

.

Вязкость капельных жидкостей снижается с возрастанием температуры, у газов – растет. При умеренном давлении вязкость газов от давления не зависит, однако, начиная с некоторого давления, вязкость возрастает при его увеличении.

Причины разных зависимостей от температуры для газов и жидкостей в том, что вязкость газов имеет молекулярно-кинетическую природу, а капельных жидкостей зависит от сил сцепления между молекулами.

В ряде процессов химической технологии капельная жидкость при движении соприкасается с газом (или паром) или с другой капельной жидкостью, практически не смешивающейся с первой.

Силовое взаимодействие молекул, которые находятся на поверхности жидкости, и молекул, расположенных вдали от нее, неодинаково. Молекула, расположенная на поверхности, находится в симметричном силовом состоянии, верхняя часть силового поля ее вынуждена взаимодействовать с молекулами, находящимися под поверхностью. В результате этого потенциальная энергия связи в поверхностном слое увеличивается, а сам слой находится в более напряженном состоянии. Это явление называют поверхностным натяжением.

Потенциальная энергия связи в поверхностном слое равна

,

где s - коэффициент поверхностного натяжения; dF - представляет собой поверхность жидкости, имеющей порядок dl².

Энергию dE можно представить как некоторую силу, совершающую работу на пути dl, поэтому

dZdl=s dl²

или

dZ=s dl.

Таким образом, поверхность жидкости стягивается силой dZ пропорциональной длине, на которой она действует. Эту силу называют силой поверхностного натяжения.

Поверхностное натяжение проявляется в том, что выделенный объем жидкости стремится принять сферическую форму, особенно это заметно на малых объемах – каплях. Действие силы поверхностного натяжения приводит к увеличению давления внутри капли, направленного внутрь жидкости по нормали к ее поверхности.

Поверхностное натяжение уменьшается с увеличением температуры. С величиной связаны характеристики смачивания капельными жидкостями твердых материалов. Смачивание оказывает существенное влияние на гидродинамические условия протекания процессов в абсорбционных и ректификационных аппаратах, конденсаторах и т.п.

Поверхностное натяжение значительно влияет на диспергирование одной жидкости в другой, с ней не смешивающейся, и поэтому существенно сказывается на гидродинамических условиях проведения процессов жидкостной экстракции.

Гидравлика

Гидромеханические процессы, связанные с перемещением жидкостей, сжатием и перемещением газов иногда называют гидравлическими по названию раздела гидромеханики – гидравлике, рассматривающей жидкости и газы как рабочие тела различных технических систем.

Гидравлика представляет собой науку, изучающую законы равновесия и механического движения жидкостей и разрабатывающую методы применения этих законов для различных прикладных задач.

Гидравликой рассматриваются вопросы покоя и движения жидкостей в двух разделах – гидростатике и гидродинамике. Гидростатика рассматривает законы равновесия в состоянии покоя, гидродинамика – законы движения жидкостей и газов.

Гидростатика

В гидростатике равновесие жидкостей рассматривается в состоянии относительного покоя, при котором в движущейся жидкости ее частицы не перемещаются друг относительно друга. Силы внутреннего трения отсутствуют, поэтому жидкость можно считать идеальной.

В состоянии покоя форма объема жидкости не изменяется и подобно твердому телу перемещается как единое целое.

Независимо от вида покоя на жидкость действуют силы тяжести и давления. В случае относительного покоя необходимо учитывать силу инерции переносного движения жидкости. Соотношение между силами, действующими на жидкость, которая находится в состоянии покоя, определяющему условия равновесия жидкости, выражается дифференциальными уравнениями равновесия Эйлера.

Дифференциальные уравнения равновесия Эйлера. В объеме жидкости, находящейся в покое (рис. 2.2), выделим элементарный параллелепипед объемом dV c ребрами dx, dy, dz, расположенными параллельно осям координат x, y, и z .

	Рис. 2.2. К выводу дифференциальных уравнений равновесия Эйлера

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю.

Запишем уравнения равновесия для осей :

;

;

.

Раскрыв скобки, получим:

;

;

.

После преобразований получим дифференциальные уравнения Эйлера:

; ; .

Для нахождения закона распределения давления во всем объеме покоящейся жидкости p=f(x, y, z) необходимо проинтегрировать систему уравнений.

Основное уравнение гидростатики. Из уравнений следует, что p=f(z), т.к. и , иначе жидкость должна была бы двигаться по горизонтали.

В этом случае частная производная 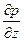изменяется на полную производную , тогда ,

, ,

или

.

После интегрирования

(2.1)

для двух произвольных горизонтальных плоскостей 1 и 2 основное уравнение гидростатики имеет вид

.

Это уравнение можно записать как

или

. (2.2)

Уравнение (2.2) является выражением закона Паскаля,согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается одинаково всем точкам ее объема.

При изменении p₀ в точке z₀ на какую-либо величину давление p во всякой другой точке изменяется на эту же величину (рис. 2.3).

Рис. 2.3. К основному уравнению гидростатики

2.2.2. Практическое приложение уравнения гидростатики

Принцип сообщающихся сосудов. Пусть два открытых сообщающихся сосуда заполнены жидкостью плотностью 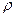(рис. 2.4).

Рассмотрим произвольную плоскость сравнения 0 - 0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то, согласно уравнению (2.2), давление в этой точке равно:

.

Если считать точку А принадлежащей правому сосуду, то давление в ней равно:

( 0, т.к. плоскость 0 - 0 проходит через точку А).

При равновесии для каждой точки давление одинаково в любом направлении, иначе бы происходило перемещение жидкости. Следовательно

или

.

Аналогичный вывод можно сделать, если рассмотреть сообщающиеся сосуды, в которых давление над свободной поверхностью жидкости одинаково.

Рис. 2.4. Условия равновесия в сообщающихся сосудах:

а – однородная жидкость; б – разнородные (несмешивающиеся) жидкости

Таким образом, в открытых или закрытых сообщающихся сосудах, находящихся под одинаковым давлением и заполненных однородной жидкостью, уровни последней располагаются на одной высоте независимо от формы и поперечного сечения сосудов.

Если сосуды заполнены одной жидкостью плотностью 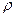, но давления над уровнем жидкости в них неодинаковы и равны и , то

откуда

. (2.3)

Уравнение (2.3) применяется при измерении давлений или разностей давлений с помощью дифференциальных -образных манометров.

Пневматическое измерение количества жидкости в подземных резервуарах. Для контроля за количеством жидкости в подземном резервуаре устанавливают трубу, нижний конец которой доходит почти до днища. Давление над жидкостью в резервуаре равно .

По трубе подают сжатый воздух или другой газ, постепенно повышая его давление, измеряемое манометром. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать через слой жидкости, давление, измеряемое манометром, перестанет возрастать и станет равным:

.

Отсюда уровень жидкости в резервуаре равен:

.

По величине и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.

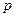Гидростатические машины. На использовании основного уравнения гидростатики основана работа гидравлических прессов, домкратов, гидроцилиндров и др. Если в гидропрессе (рис. 2.5) приложить небольшое усилие к поршню 1, перемещаемому в цилиндре меньшего диаметра , и создать давление на поршень, то, согласно закону Паскаля, такое же давление 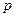будет приходиться на поршень 2 в цилиндре с большим диаметром , при этом сила давления на поршень 1 составит

,

а сила давления на поршень 2

.

В результате поршень в цилиндре большего диаметра передает силу давления во столько раз большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, насколько поперечное сечение цилиндра 2 больше, чем цилиндра 1.

Давление жидкости на дно и стенки сосуда. Если жидкость помещена в сосуд любой формы, то гидростатическое давление во всех точках горизонтального дна сосуда одинаково, а давление на боковые стенки возрастает с увеличением глубины погружения.

Гидростатическое давление на дно сосуда в соответствии с уравнением гидростатики

,

где 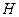– высота жидкости в сосуде.

Сила давления на горизонтальное дно не зависит от формы сосуда и объема жидкости в нем и определяется лишь только высотой столба жидкости и площадью дна сосуда:

.

Гидростатическое давление жидкости на вертикальную стенку изменяется по высоте. Сила давления на стенку рассчитывается по формуле

,

где – расстояние от верхнего уровня жидкости до центра тяжести смоченной площади F стенки.

Гидродинамика

Движущей силой при течении жидкости является разность давлений, которая создается с помощью насосов или компрессоров, либо вследствие разности уровней или плотностей жидкости.

Знание законов гидродинамики позволяет находить Δp, необходимое для перемещения заданного количества жидкости с требуемой скоростью, а значит и расход энергии на это перемещение. И наоборот, определить скорость и расход жидкости при заданном Δp.

Различают внутреннюю, внешнюю и смешанную задачи гидродинамики.

К внутренней задаче гидродинамики относятся вопросы изучения закономерностей движения жидкости и газов внутри труб и каналов. Внешняя задача связана с изучением закономерностей обтекания жидкостями и газами различных тел (процессы осаждения, механического перемешивания и т.д.). Смешанная задача заключается в изучении движения жидкости и газов через зернистые и пористые слои твердых материалов. Жидкость в этом случае движется одновременно внутри каналов сложной формы и обтекает твердые частицы (процессы фильтрования, течения жидкостей и газов через насадки массообменных аппаратов, реакторов с твердым катализатором и т.п.).