Методика структурного синтеза
Задача структурного синтеза автоматов заключается в построении структурной схемы в виде композиции более простых автоматов, называемых элементарными, автоматами (ЭА) и комбинационных логических схем (КЛС).
Обычно в качестве ЭА выбираются автоматы Мура с двумя состояниями, которые должны удовлетворять требованиям полноты по переходам и выходам. В свою очередь КЛС должны удовлетворять требованию функциональной полноты реализуемых функций алгебры логики (ФАЛ). Наиболее известным методом решения данной задачи является канонический метод структурного синтеза [2, З], предусматривающий выполнение следующих шагов.
Шаг 1. Выбор набора элементарных автоматов (ЭА) Мура и системы логических элементов; наименьшее число ЭА определяется величиной ]log2n[, где n – число внутренних состояний автомата.
Шаг 2. Кодирование входных, выходных сигналов и внутренних состояний автомата; для борьбы с «состязаниями» ЭА применяется методика противогоночного кодирования, предотвращая любую возможность перехода в «чужое» состояние под воздействием входных сигналов; в результате строится кодированная таблица (проще -кодированный граф) переходов и выходов.
Шаг 3. Формирование по имеющейся кодированной таблице (графу) переходов и выходов функций возбуждения для каждого ЭА и выходных функций в виде соответствующих ФАЛ; синтез входной и выходной КЛС; для этой цели применяются классические методы минимизации ФАЛ.
В дополнение к каноническому методу структурного синтеза приведем ряд практических рекомендаций, учитывающих особенности современного элементного базиса и направленных на повышение эффективности синтезируемых относительно простых (см. варианты заданий) автоматов:
1. Выбор типа триггера в качестве ЭА оказывает вполне определенное влияние как на сложность реализации входной логики, так и конструкцию автомата в целом. На рис. 2.1 приведены графы переходов наиболее распространенных триггеров с одним входом.

Рис. 2.1. Граф схемы переходов: а) Т–триггера, б) D–триггера
Если граф переходов автомата содержит большое число петель возврата, то выбор D — триггера может привести к некоторому усложнению функций возбуждения. Такая ситуация возникает, если единичное состояние D — триггера соответствует коду возвратного
состояния автомата. Как видно из рис. 2.1,б для сохранения этого состояния на вход D — триггера необходимо падать логическую единицу. Однако окончательное заключение о сложности входной КЛС можно сделать лишь по окончании ее синтеза с использованием как D–триггера, так и Т–триггера.
2. Еще труднее оценить сложность получаемой конструкции автомата по числу корпусов используемых микросхем (кристаллов).
При большом числе состояний автомата обычно выгоднее использовать D–триггеры. Так, микросхема ТМ8 серии К155 представляет из себя регистр из 4 D–триггеров (рис. 2.2), а микросхема ТМ9 той же серии – регистр из 6 D–триггеров, имеющих общие цепи синхронизации и установки в 0-е состояние.
Для получения Т–триггера лучше взять многоцелевой JK–триггер, объединив его J, К – входы на Т–вход. Оставшиеся R, S – входы могут использоваться для установки триггера в исходное состояние. Другие способы взаимного преобразования триггеров приводятся на стр. 73 в [5]. Следует заметить, что в одном корпусе микросхемы размещается меньшее число JК – триггеров (не более двух для микросхем серий К155, К555, К531). Поэтому, если граф переходов автомата имеет относительно небольшое число состояний и почти не содержит петель, предпочтение можно отдать использованию JK–триггера в качестве Т–триггера.
3. Необходимость борьбы с гонками в автомате не следует преувеличивать особенно тогда, когда время переключения триггеров (десятки, нс) много меньше периода поступления входных сигналов. Если же автомат (например, кодовый преобразователь) работает в реальном времени, предлагается кодировать состояние автомата, начиная с минимального числа триггеров (]log2n[) и в случае возникновения гонок последовательно увеличивать это число на 1.
4. С точки зрения упрощения входной КЛС определенный эффект может дать следующий прием. Наиболее «популярные» состояния (по числу заходящих дуг) абстрактного автомата предлагается кодировать наименьшим числом единиц.
Необходимо также предусмотреть возможность принудительной установки автомата в начальное состояние. Поэтому его необходимо закодировать с учетом условия установки всех триггеров в соответствующее состояние одним сигналом (Т или S). Можно также предусмотреть дополнительную возможность автоматической установки автомата в начальное состояние при выключении питания.
5. Для того чтобы не прибегать к построению громоздкой кодированной таблицы переходов, предлагается следующий прием формирования ДНФ функций возбуждения непосредственно по граф-схеме переходов автомата (см. рис. 3.4).
Пусть тип ЭА выбран и все состояния закодированы. Тогда, сравнивая коды смежных или возвратных (с петлями) состояний, для выбранного типа триггера (см. рис. 2.1) решается вопрос о необходимости подачи на вход i-гo триггера единичного сигнала Vi=l. Этот факт отражается на соответствующей дуге граф-схемы переходов меткой Vi,. Искомая функция возбуждения для i-гo триггера определяется совокупностью (сбором) всех меток Vi, каждой из которых

Рис. 2.2. Примеры микросхем традиционных серий типа ТТЛ и ТТЛШ
сопоставляется конъюнкция состояний триггеров для исходящего (левого по дуге) состояния и входных (на дуге) сигналов. Для абстрактной модели Мили формирование ДНФ функций выходов осуществляется аналогичным путем.
6. В отличие от канонического метода синтеза следует не прибегать к «уплотняющему» двоичному кодированию входных и выходных сигналов, если последние имеют явный физический смысл (например, состояния кнопок, вход двоичного числа, фиксирующие и установочные сигналы) лишь при использовании на входе автомата предварительного синтезированного шифратора. Искусственное уменьшение числа входных/выходных сигналов, достигаемое за счет двоичного кодирования, создает лишь видимость упрощения автомата и не решает вопроса о последующем декодировании периферийных сигналов.
7. Если автомат содержит большое число выходов, то иногда бывает выгодно исходить из абстрактной модели Мура. Тогда каждый выходной сигнал определяется конъюнкцией состояний триггеров, определяющих соответствующее состояние автомата. Следует также рассмотреть вариант использования на входе автомата стандартной микросхемы дешифратора.
8. Синтез входной и выходной КЛС следует проводить с учетом свойств реальной элементной базы (см. рис. 2.2). Если формируемые ФАЛ содержат не более 5 – 6 переменных, их минимизацию проще всего проводить с использованием наглядных диаграмм Вейча или карт Карно (Карнау).
Полученные минимальные ДНФ следует преобразовать с использованием скобочных форм и правил де Моргана к виду, позволяющему применить схемы типа И, ИЛИ, составные логические схемы и мультиплексоры ТТЛ [5].
Дополнительные соображения на этот счет и эффективные приемы синтеза КЛС приводятся в практическом пособии И.С. Потемкина [б].
9. Качество синтезируемого автомата можно еще более повысить, если перейти к использованию настраиваемых логических микросхем повышенного уровня интеграции. К их числу относятся программируемые логические матрицы (ПЛМ), составляющие основу построения большинства управляющих схем микропроцессорных комплектов [4].
Структура ПЛМ определяется двумя матрицами М1=K 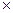 L, M2=L
L, M2=L 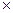 F где К—число входов (входных шин), L—число элементарных конъюнкций (минитермов), ДНФ, F—число выходов (выходных функций). Предполагается, что внутри микросхемы каждый вход имеет инверсную шину, отмечаемую жирной черточкой (инвертором). Результат программирования ПЛМ представляется точками (соединениями) на пересечении соответствующих строк и столбцов Ml, M2. В случае если логика матриц Ml, M2 реализуется в терминах элементарных функций
F где К—число входов (входных шин), L—число элементарных конъюнкций (минитермов), ДНФ, F—число выходов (выходных функций). Предполагается, что внутри микросхемы каждый вход имеет инверсную шину, отмечаемую жирной черточкой (инвертором). Результат программирования ПЛМ представляется точками (соединениями) на пересечении соответствующих строк и столбцов Ml, M2. В случае если логика матриц Ml, M2 реализуется в терминах элементарных функций 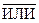 , следует помнить, что на входы Ml должны поступать инверсии входных сигналов, а выходы M2 заранее проинвертированы.
, следует помнить, что на входы Ml должны поступать инверсии входных сигналов, а выходы M2 заранее проинвертированы.
Будем считать, что синтезируемый автомат реализуется на ПЛМ с произвольной, но обозримой структурой соединений (заказной БИС). Можно также ориентироваться и на использование стандартных ПЛМ. В качестве примера назовем отечественную ПЛМ КР556РТ1, со структурой М1=16 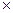 48, М2=48
48, М2=48 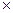 8. Вопросы повышения эффективности синтеза микропрограммных автоматов на ПЛМ достаточно подробно изложены в [3]. Здесь мы предлагаем использовать ПЛМ для синтеза автоматов более широкого класса.
8. Вопросы повышения эффективности синтеза микропрограммных автоматов на ПЛМ достаточно подробно изложены в [3]. Здесь мы предлагаем использовать ПЛМ для синтеза автоматов более широкого класса.
Большая часть из приведенных рекомендаций носит многоальтернативный характер. Поэтому в процессе проектирования желательно синтезировать несколько логических схем, воплощающих искомый автомат.
КОНТРОЛЬНЫЙ ПРИМЕР
Задание. Построить логическую схему последовательного компаратора для сравнения 2 двоичных чисел А, В произвольной длины, поступающих на вход, начиная с младших разрядов. По окончании подачи чисел А, В на вход компаратора на его выходе должны появиться сигналы: y0, если А=В, y1 если A<B, у2 если A>B, у3.
Решение.
1. Введем в рассмотрение входные буквы: x00, х11, x01, х10, где нижний первый индекс соответствует значению текущего разряда числа А, а второй — числа В. С точки зрения сравнения чисел А, В действие букв x00, х11 равносильно, что позволяет их рассматривать как одну букву, обозначаемую в дальнейшем x0.
2. Формализуем условия работы искомого автомата на языке регулярных выражений, эти условия приобретают вид:
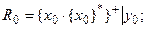 (3.1)
(3.1)
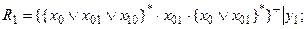 (3.2)
(3.2)
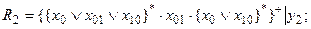 (3.3)
(3.3)
Здесь итерационные скобки { }+={ }*e, где е – пустая буква,
введена для сокращения длины записи регулярных выражений.
Полученный граф — рис. 3.1 содержит три финитные вершины 1, 3, 4, соответствующие выходным реакциям у0, y1, y2.
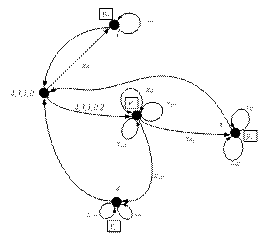
Рис. 3.1. Обобщенный граф регулярных выражений (3.1) – (3.3)
«Нейтральная» вершина 2 помечена пустой буквой е. Каждая финитная вершина с помощью пустой стрелки замыкается на начальную вершину, что соответствует воспроизведению итерационных скобок { }+. Номера вершин, «переносимых» по пустым стрелкам выписаны через запятую слева относительно вершин 0 и 2.
3. Переходим к построению обобщенного графа регулярных выражений (3.1) – (3.3).
4. Применяя методику детерминизации графа регулярных выражений (раздел 1.1), приходим к табл. 3 I.
Таблица 3.1
| Вых. | – | 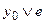 | 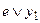 | 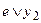 |
| Сост. | 1 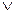 2 2 | 2 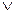 3 3 |
x0 1 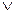 2 1
2 1 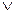 2 2
2 2 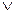 3 2
3 2 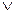 4
4
x01 2 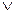 3 2
3 2 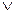 3 2
3 2 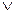 3 2
3 2 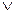 3
3
x10 2 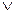 4 2
4 2 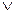 4 2
4 2 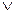 4 2
4 2 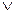 4
4
Отсутствие противоречий при определении дизъюнкций выходных сигналов в табл. 3.1 свидетельствует о том, что система регулярных выражений (3.1) – (3.3) является корректной.
В дальнейшем при определении реакций автомата y0, y1, y2 пустой символ, е можно не учитывать.
5. Переходим к эквивалентному автомату Мили, открывающему возможность получения абстрактной схемы наименьшей сложности (по числу состояний). Первоначальная модель содержит 4 состояния: 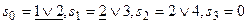 . Так как разбиение
. Так как разбиение 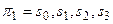 не поддается расщеплению (совпадает с разбиением
не поддается расщеплению (совпадает с разбиением 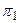 ), убеждаемся, что изображенный на рис. 1.2 – минимальный автомат.
), убеждаемся, что изображенный на рис. 1.2 – минимальный автомат.
6. Для проверки результатов абстрактного синтеза, а в случае неудачи (несоответствие поведения автомата техническому заданию, отсутствие видимых способов получения корректного описания), индуктивно воспроизводим дерево управления искомого автомата – рис. 1.1. Приняты следующие соглашения. Каждый «веер» ребер слева направо определяется входными буквами 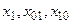 соответственно. Все ребра дерева помечены цифрами 0, 1, 2, соответствующими выходным реакциям
соответственно. Все ребра дерева помечены цифрами 0, 1, 2, соответствующими выходным реакциям 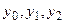 . Дерево построено в предположении, что r=1, d=1, и потому имеет высоту h==3.
. Дерево построено в предположении, что r=1, d=1, и потому имеет высоту h==3.
На дереве ясно просматриваются 3 различимые вершины 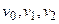 базиса. Остальные зачеркнутые на рис. 1.1 вершины не отличимы от вершин базиса. Свертки дерева управления приводят к точной копии искомого автомата (рис. 1.2).
базиса. Остальные зачеркнутые на рис. 1.1 вершины не отличимы от вершин базиса. Свертки дерева управления приводят к точной копии искомого автомата (рис. 1.2).
Заметим, что все дуги, входящие в каждое из его состояний, помечены одинаковыми реакциями. Следовательно, граф на рис. 1.2 можно также рассматривать и как автомат Мура (рис. 3.2), что может дать некоторые преимущества на этапе структурного синтеза.
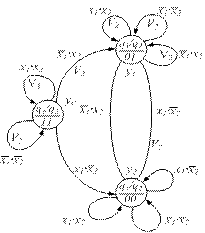
Рис. 3.2. Кодированный граф переходов
7. В качестве элементарного автомата выбираем D-триггер. Минимально возможное число D-триггеров – ]log23[=2. Рассмотрим вариант неудачного кодирования состояний абстрактного автомата: 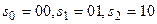 , который приводит, во-первых, к усложнению КЛС, во-вторых, к возникновению состязаний ЭА. Так, при переключении из состояния
, который приводит, во-первых, к усложнению КЛС, во-вторых, к возникновению состязаний ЭА. Так, при переключении из состояния 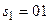 в состояние
в состояние 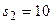 под воздействием
под воздействием 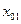 для промежуточного состояния
для промежуточного состояния 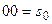 на выходе автомата будет получен сигнал
на выходе автомата будет получен сигнал 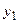 вместо требуемого сигнала
вместо требуемого сигнала 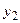 . Значительно более удачным является вариант кодирования, представленный на рис. 3.2.
. Значительно более удачным является вариант кодирования, представленный на рис. 3.2.
Каждому состоянию автомата приписано единичное значение одного из выходов 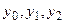 . На рис. 3.2 также показаны: комбинации двоичных входов
. На рис. 3.2 также показаны: комбинации двоичных входов 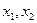 определяющие поразрядные значения чисел А и В; единичные значения функций возбуждения
определяющие поразрядные значения чисел А и В; единичные значения функций возбуждения 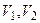 для 1-го и 2-го D-триггеров соответственно.
для 1-го и 2-го D-триггеров соответственно.
8. Как видно из кодированного графа переходов – рис. 3.2:
Нетрудно также получить функцию возбуждения
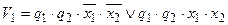
Функция V2 содержит 8 минитермов. Попытаемся ее минимизировать. Для этого воспользуемся диаграммой Вейча — рис. 3.3, где тонкими овалами выделены группы минитермов, образующих простые импликанты. В результате минимизации ФАЛ V2 получаем
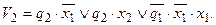
9. Взяв за основу микросхемы серии К155 (см. [6] или рис, 2.2), обеспечивающие реализацию полученных в п. 8 функций, получаем один из вариантов логической схемы искомого автомата – рис. 3.4. Здесь для обозримости схемы принят графический прием вложения всех соединений в некоторую гипотетическую магистраль (жирная линия на рис. 3.4) с установлением строгого соответствия между одинаково пронумерованными входами и выходами. Как видно из рис. 3.4, для реализации последовательного компаратора требуется 5 корпусов или кристаллов.
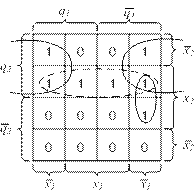
Рис. 3.3. Диаграмма Вейча для функции V2
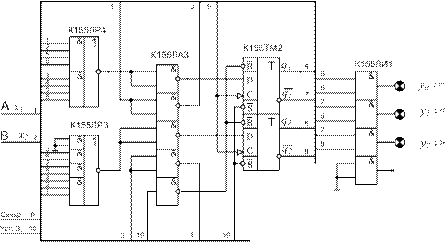
Рис. 3.4. Логическая схема компаратора (Вариант - 1)
10. Проверим возможность повышения качества синтеза за счет использования ПЛМ. Для реализации функций возбуждения 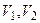 необходимо пять вертикальных шин матрицы Ml (по общему числу минитермов). Выходную логику также выгодно вложить в ПЛМ. Для этого перейдем к автоматной модели Мили (рис. 1.2), принимая представленный на рис. 3.4 вариант кодирования состояний входных сигналов автомата. В соответствии с п. 5 раздела 3 убеждаемся в том, что функция
необходимо пять вертикальных шин матрицы Ml (по общему числу минитермов). Выходную логику также выгодно вложить в ПЛМ. Для этого перейдем к автоматной модели Мили (рис. 1.2), принимая представленный на рис. 3.4 вариант кодирования состояний входных сигналов автомата. В соответствии с п. 5 раздела 3 убеждаемся в том, что функция 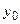 в точности совпадает с функцией
в точности совпадает с функцией 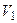 . В свою очередь каждая из функций
. В свою очередь каждая из функций 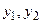 содержит по 5 минитермов и после минимизации приобретает вид:
содержит по 5 минитермов и после минимизации приобретает вид:
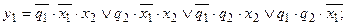
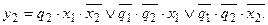
Для реализации всех полученных функций необходима ПЛМ со структурой 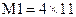 ,
, 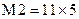 . В результате настройки ПЛМ на указанные функции получаем 2-й вариант логической схемы — рис. 3.5, который легко размещается на 2 кристаллах.
. В результате настройки ПЛМ на указанные функции получаем 2-й вариант логической схемы — рис. 3.5, который легко размещается на 2 кристаллах.
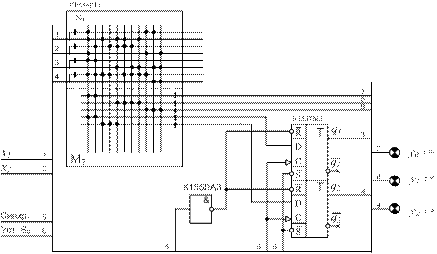
Рис. 3.5. Логическая схема компаратора (Вариант - 2)
Итак, мы раскрыли многие тонкости сквозного проектирования управляющего автомата с конечным числом состояний. Для того чтобы получить и обосновать Ваш проект управляющего автомата необходимо рассмотреть, по меньшей мере, 2 – 3 варианта его абстрактной и структурной реализации. Многоальтернативный синтез рекомендуется проводить с использованием пакета программ, именуемого SANAR [9] и разработанного студентами потока кафедры ВМСиС.
ВАРИАНТЫ ТИПОВОГО ЗАДАНИЯ
1. Построить логическую схему последовательного компаратора для сравнения 2 двоичных чисел А, В произвольной длины, поступающих на вход, начиная со старших разрядов. По сигналу окончания подачи чисел — сигналу 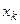 на выходе компаратора должны появиться сигналы 0, если А=В, 1, если А<В, 2, если А>В.
на выходе компаратора должны появиться сигналы 0, если А=В, 1, если А<В, 2, если А>В.
2. Построить накапливающий сумматор для формирования поразрядных сумм и переносов в темпе поступления на вход сумматора 2 двоичных чисел произвольной длины, начиная с младших разрядов.
Указание: При построении «тестового» дерева управления исходить из предположения, что 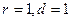 .
.
3. Построить логическую схему последовательной свертки по mod 3 двоичного числа, которое поступает на вход схемы, начиная со старших разрядов. Для считывания результата (чисел 0, 1, 2) и автоматической установки схемы в начальное состояние ввести сигнал 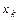 .
.
4. Построить логическую схему последовательной свертки по mod 7 двоичного числа, подаваемого на вход схемы со старших разрядов. Результат (числа от 0 до 6) должен появляться на выходе схемы в темпе поступления двоичного числа разряд за разрядом.
Указание: Воспользоваться методом свертки дерева управления, если известно, что 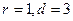
5. Построить автомат для управления освещением 2 комнат. Расположение комнат K1, K2 и дверей показано на рис. 4.1. Вход человека в K1 и K2 сопровождается выработкой входных сигналов 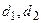 а его выход из K1, K2 – сигналов соответственно
а его выход из K1, K2 – сигналов соответственно 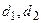 . Предполагается, что двери не могут срабатывать одновременно. В K1 и K2 могут находиться n1 и n2 человек. Лампочки Л1, Л2 должны гореть лишь в том случае, если в K1 или в К2 находится хотя бы один человек. Вариант построения автомата выбрать из табл. 4.1.
. Предполагается, что двери не могут срабатывать одновременно. В K1 и K2 могут находиться n1 и n2 человек. Лампочки Л1, Л2 должны гореть лишь в том случае, если в K1 или в К2 находится хотя бы один человек. Вариант построения автомата выбрать из табл. 4.1.
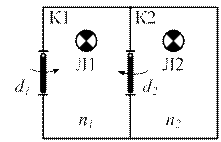
Рис. 4.1. План расположения комнат и дверей
Таблица 4.1
| Вариант | n1 | n2 | n1+n2 |
| 5.1 | |||
| 5.2 | |||
| 5.3 | |||
| 5.4 |
Указание: Выходные сигналы автомата целесообразно представить следующим образом:
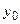 – Л1 и Л2 не горит,
– Л1 и Л2 не горит,
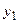 – Л1 горит, Л2 не горит,
– Л1 горит, Л2 не горит,
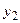 – Л1 не горит, Л2 горит,
– Л1 не горит, Л2 горит,
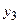 – Л1 и Л2 горят
– Л1 и Л2 горят
6. Построить логическую схему электронного кодового замка, который должен открываться (сигнал 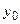 ) при нажатии заданного числа раз n1– первой, n2– второй, n3 – третьей кнопок. При неправильном нажатии кнопок должен вырабатываться сигнал тревоги (сигнал
) при нажатии заданного числа раз n1– первой, n2– второй, n3 – третьей кнопок. При неправильном нажатии кнопок должен вырабатываться сигнал тревоги (сигнал 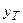 ). Учесть необходимость автоматической установки автомата в начальное состояние. Вариант нажатия кнопок выбрать из табл. 4.2.
). Учесть необходимость автоматической установки автомата в начальное состояние. Вариант нажатия кнопок выбрать из табл. 4.2.
Таблица 4.2
| Вариант | n1 | n2 | n3 |
| 6.1 | |||
| 6.2 | |||
| 6.3 | |||
| 6.4 |
7. Автомат для продажи билетов работает при получении жетонов достоинством 5 и 10 руб. В 1-м случае автомат выдает билет, если жетонный накопитель, вмещающий m рублевых жетонов, не заполнен; в противном случае автомат жетонов не принимает и билета не выдает. При получении 10 рублевого жетона автомат выдает билет и 5 рублевый жетон сдачи, если в приемнике есть хотя бы один 5 рублевый жетон.
Синтезировать описанный автомат для одного из вариантов табл. 4.3.
Таблица 4.3
| Вариант | m |
| 7.1 | |
| 7.2 | |
| 7.3 |
8. Построить логическую схему тренажера, предназначенного для обучения операторов работе на пульте. Пульт имеет 4 кнопки 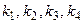 , которые должны включаться в строго определенной последовательности. При правильном нажатии кнопок вырабатывается сигнал W, при неправильном – сигнал N. По окончании сеанса схема должна автоматически устанавливаться в начальное состояние. Одну из последовательностей нажатия кнопок выбрать из табл. 4.4.
, которые должны включаться в строго определенной последовательности. При правильном нажатии кнопок вырабатывается сигнал W, при неправильном – сигнал N. По окончании сеанса схема должна автоматически устанавливаться в начальное состояние. Одну из последовательностей нажатия кнопок выбрать из табл. 4.4.
Таблица 4.4
| Вариант | Последовательность |
| 8.1 | 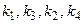 |
| 8.2 | 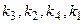 |
| 8.3 | 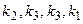 |
| 8.4 | 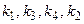 |
9. Построить логическую схему электронной игрушки, имитирующей выработку условного рефлекса ( 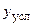 ) у животного в ответ на воздействие безусловного (буква b) и условного (буква u) раздражителей. Совместное воздействие указанных раздражителей определяется буквой с. Игрушка характеризуется следующими параметрами: k –минимально возможное число букв c, необходимых для выработки
) у животного в ответ на воздействие безусловного (буква b) и условного (буква u) раздражителей. Совместное воздействие указанных раздражителей определяется буквой с. Игрушка характеризуется следующими параметрами: k –минимально возможное число букв c, необходимых для выработки 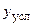 в процессе обучения, l, m —число несовпадений раздражителей (либо b, либо u), что приводит к потере полученного навыка соответственно в процессе обучения и по окончании такового. Вариант построения автомата выбрать из табл. 4.5.
в процессе обучения, l, m —число несовпадений раздражителей (либо b, либо u), что приводит к потере полученного навыка соответственно в процессе обучения и по окончании такового. Вариант построения автомата выбрать из табл. 4.5.
Таблица 4.5
| Вариант | k | l | m |
| 9.1 | |||
| 9.2 | |||
| 9.3 |
10. Построить охранный автомат, который каждый раз при поступлении серий из n, n+1 сигналов s1 формирует на выходе сигнал 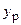 («предупреждение»). В случае поступления сигнала s2 после серии сигналов s1, большей или равной m, на выходе появляется сигнал
(«предупреждение»). В случае поступления сигнала s2 после серии сигналов s1, большей или равной m, на выходе появляется сигнал 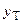 («тревога») и автомат устанавливается в начальное состояние. Вариант автомата выбрать из табл. 4.6.
(«тревога») и автомат устанавливается в начальное состояние. Вариант автомата выбрать из табл. 4.6.
Таблица 4.6
| Вариант | n | m |
| 10.1 | ||
| 10.2 | ||
| 10.3 |
11. Синтезировать распознающий автомат для сортировки изделий, передвигающихся на конвейере, по их длине. Датчики 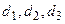 вырабатывают сигналы а, b, с (инверсные сигналы
вырабатывают сигналы а, b, с (инверсные сигналы 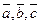 ) в случае появления (исчезновения) изделия, проходящего мимо соответствующей опоры. Фрагмент выдачи сигналов а и b показан на рис. 4.2. Разбраковка изделий по длине определяется следующими выходными сигналами:
) в случае появления (исчезновения) изделия, проходящего мимо соответствующей опоры. Фрагмент выдачи сигналов а и b показан на рис. 4.2. Разбраковка изделий по длине определяется следующими выходными сигналами:
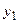 , если l < l0 ;
, если l < l0 ; 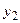 , если l0 ≤ l ≤ 2 l0 ;
, если l0 ≤ l ≤ 2 l0 ; 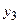 , если l >2 l0 .
, если l >2 l0 .
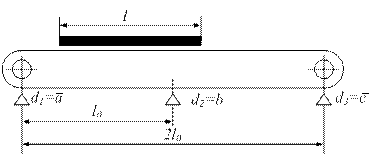
Рис. 4.2. Схема расположения датчиков на конвейере
12. Синтезировать комплектующий автомат, принимающий блоки А, В, С, ..., расположенные на конвейере l в случайном порядке, и пропускающий их на конвейер 2 с целью формирования сборочных комплектов K1, K2, ..., так как это показано на рис. 4.3.
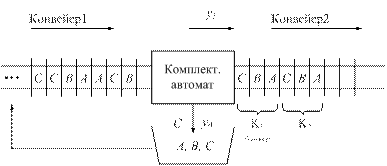
Рис. 4.3. Схема формирования комплектов деталей на конвейере
Сборочные комплекты состоят из заданного числа блоков каждого типа, расположенных в строго определенной последовательности. На выходе автомата вырабатываются сигналы 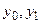 соответственно обеспечивающие сброс ненужного блока в бункер или пропуск недостающего блока на конвейер 2. Вариант реализуемого автомата выбрать из табл. 4.7.
соответственно обеспечивающие сброс ненужного блока в бункер или пропуск недостающего блока на конвейер 2. Вариант реализуемого автомата выбрать из табл. 4.7.
Таблица 4.7
| Вариант | Последовательность блоков в комплекте |
| 12.1 | A С В D А |
| 12.2 | А В В С С А |
| 12.3 | В В А С D В |
13. Построить дешифратор, на выходе которого вырабатывается десятичный эквивалент в темпе поступления соответствующего двоичного числа, начиная со старших разрядов. Окончание поступления разрядов двоичного числа фиксируется сигналом 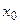 . Один из вариантов построения дешифратора выбрать из табл. 4.8.
. Один из вариантов построения дешифратора выбрать из табл. 4.8.
Таблица 4.8
| Вариант | n |
| 13.1 | |
| 13.2 |
14. Построить счетчик по mod k, на вход которого поступают одиночные единичные сигналы, соответствующие некоторому числу в унарном коде. Вариант счетчика выбрать из табл. 4.9.
Таблица 4.9
| Вариант | k |
| 14.1 | |
| 14.2 |
15. Построить счетчик, осуществляющий счет одиночных единичных сигналов либо по mod 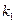 , либо по mod
, либо по mod 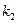 в зависимости от значения установочного сигнала u. Вариант счетчика выбрать из табл. 4.10.
в зависимости от значения установочного сигнала u. Вариант счетчика выбрать из табл. 4.10.
Таблица 4.10
| Вариант | mod 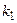 | mod 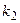 |
| 15.1 | ||
| 15.2 | ||
| 15.3 |
Указание: Для описания работы счетчика построить объединенное дерево управления, поставив в соответствие каждой левой ветви отсутствие сигнала, средней ветви наличие сигнала по 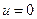 , правой ветви наличие сигнала по
, правой ветви наличие сигнала по 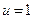 .
.
16. Построить реверсивный счетчик, осуществляющий либо сложение, либо вычитание одиночных единичных сигналов в зависимости от задания режима его работы, (Вариант построения счетчика выбрать по табл. 4.9).
17. Построить логическую схему торгующего автомата для выдачи товаров двух типов, имеющих стоимость либо c1, либо c2 в зависимости от значения установочного сигнала 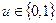 . На вход автомата могут поступать монеты достоинством 1, 2, 5. Вариант автомата выбрать из табл. 4.11.
. На вход автомата могут поступать монеты достоинством 1, 2, 5. Вариант автомата выбрать из табл. 4.11.
Таблица 4.11
| Вариант | c1 | c2 |
| 17.1 | ||
| 17.2 | ||
| 17.3 |
18. Синтезировать автомат, обеспечивающий выдачу товара как при точном совпадении суммы монет с заданной стоимостью с товара, так и при некотором превышении этой стоимости, если у покупателя не оказалось монет нужного достоинства d={1,2,5}. Если же покупатель ввел (второпях) неверную последовательность, превосходящую стоимость с (несмотря на наличие нужных монет), автомат должен сформировать сигнал ус—сброса принятых монет. Вариант автомата выбрать из табл. 4.12.
Таблица 4.12
| Вариант | c | Запрещенные комбинации |
| 18.1 | (1,5,2); (1,5,2);… | |
| 18.2 | (1,1,1,5,2); (5,1,1,2); (5,1,2,2);… |
19. Синтезировать автомат, обеспечивающий выдачу товара как при точном совпадении суммы монет с заданной стоимостью с товара, так и при некотором превышении этой стоимости, если у покупателя не оказалось монет нужного достоинства d={1,2,5}. Предусмотреть режим сброса неправильного набора монет при наличии «лишней» монеты, без которой стоимость товара и так обеспечивается. Вариант автомата выбрать из табл. 4.13.
Таблица 4.13
| Вариант | c |
| 19.1 | |
| 19.2 |
20. Синтезировать автомат для последовательного преобразования числа Х, подаваемого на вход автомата последовательно старшими разрядами, представленного в q–ичной системе СС, в n-разрядный двоичный код Грея (см. табл. 4.14). По окончании переработки двоичного числа автомат должен устанавливаться в начальное состояние.
Указание: Значения разрядов у, кода Грея 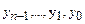 могут быть определены по правилу:
могут быть определены по правилу: 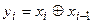 , где
, где 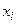 - значение разрядов двоичного числа
- значение разрядов двоичного числа 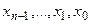 для
для 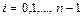
Таблица 4.14
| Вариант | q | n |
| 20.1 | ||
| 20.2 | любое | |
| 20.3 | ||
| 20.4 | ||
| 20.5 | любое |
21. Синтезировать автомат для последовательного преобразования n-разрядного двоичного числа либо, либо в код Грея, либо в его представление в q-ичной СС в зависимости от выбранного режима работы (табл. 4.15).
Таблица 4.15
| Вариант | n | q |
| 21.1 | ||
| 21.2 | ||
| 21.3 | ||
| 21.4 | любое |
22. Построить кодовый преобразователь, обеспечивающий последовательное преобразование n-разрядного кода числа в k-ичной позиционной системе счисления с натуральным основанием в m-разрядный код того же числа в l-чной позиционной системе счисления, начиная с младших разрядов (табл. 4.16).
Таблица 4.16
| Вариант | k | l | n | m |
| 22.1 | ||||
| 22.2 | ||||
| 22.3 | ||||
| 22.4 |
Указание. Для получения автоматного отображения произвести выравнивание длин входного и выходного кодов путем добавления 0 в младшие разряды кода, если n>m; в старшие разряды кода, если n<m.
23. Построить тетрадный анализатор, который при поступлении на вход любого 4-разрядного двоичного числа, начиная с младших разрядов, в случае, если это число <10, вырабатывает сигнал у1 («правильная тетрада»), а в противном случае, - у0 («неправильная тетрада»). По окончании подачи числа, анализатор должен автоматически устанавливаться в начальное состояние.
24. Синтезировать автомат, осуществляющий возведение в квадрат двоичных чисел в диапазоне [O]2 – [N]2, подаваемых на его вход последовательно, начиная с младших разрядов. Вариант автомата задается в табл. 4.17.
Таблица 4.17
| Вариант | N |
| 24.1 | |
| 24.2 | |
| 24.3 |
Указание. Применить прием приведения таблицы соответствия «Вход - Выход» к автоматному выражению за счет добавления необходимого числа 0 в старшие разряды.
25. Построить автомат, осуществляющий умножение двух двоичных чисел в диапазоне, подаваемых последовательно на абстрактный вход автомата в виде комбинации 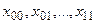 .Вариант автомата задается в табл. 4.17. При выполнении задания воспользоваться указанием к п.24.
.Вариант автомата задается в табл. 4.17. При выполнении задания воспользоваться указанием к п.24.
26. Построить автомат, осуществляющий управление грузовым лифтом посредством выполнения следующих действий: открытие дверей по сигналу x1, закрытие дверей по сигналу x2 от таймера, движение на 2,3,..., N этаж при нажатии соответствующих кнопок Кн.1, Кн.2, …, Кн.N, открытие двери по сигналу x3 от таймера, закрытие двери по сигналу x4 от таймера, спуск вниз на 1 – ый этаж, стоп. Варианты задания в табл. 4.17.
ЗАКЛЮЧЕНИЕ
С момента первого издания настоящих методических указаний прошло без малого 20 лет, но они не устарели и, более того, их актуальность возросла. В этом нет ничего удивительного, ведь теория автоматов – один из фундаментальных разделов Computer Science. Можно назвать ряд новых направлений теории вычислительных систем, становление и развитие которых «обязано» теории автоматов. Прежде всего, это универсальный язык моделирования UML (Unified Modeling Language), представляющий объектный подход к созданию системного и прикладного программного обеспечения [10]. Заслуживает внимание и такая многообещающая технология программной реализации алгоритмов как автоматное программирование[11]. Стало быть, теория автоматов важна, нужна, поэтому она требует углубленного изучения для будущих специалистов по IT технологиям. Этой цели и служит настоящее учебное пособие.
Считаю приятным долгом выразить слова признательности профессору А.Ф. Крюкову за поддержку в подготовке данного издания к печати.
