Процедура и методы анализа диагностических моделей

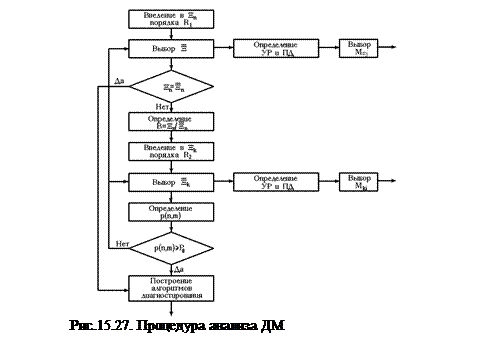
Несмотря на большое разнообразие ДМ и методов их анализа, процесс анализа ДМ может быть представлен обобщенной процедурой (рис.15.27).

Анализ ДМ начинается с формирования совокупности оцениваемых (измеряемых) диагностических признаков. ДМ любого типа содержит в явном виде множество 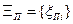, 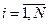прямых диагностических признаков. В качестве прямых диагностических признаков могут рассматриваться коэффициенты алгебраических или дифференциальных уравнений, операторы ветвей в графе и другие, непосредственно присутствующие в ДМ.

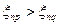Чтобы сделать обоснованный выбор диагностических признаков, необходимо их упорядочить в соответствии с выбранным критерием. Совокупность полностью упорядочивается введением отношения порядка R₁ в предположении, что , если 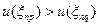; 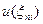определяется на элементах 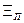и вид его зависит от специфических особенностей ЭУ. 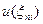можно определять через норму 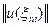. Норма – обобщающее понятие абсолютной величины (норма вектора – его длина).

В связи с технической сложностью или невозможностью измерения, а также с учетом экономической целесообразности для диагностирования часто приходится выбирать из множества 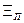совокупность 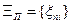, 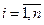; n 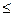N оцениваемых прямых признаков. Если 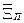= 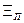, то введенный порядок позволяет непосредственно построить алгоритм диагностирования. В этом случае алгоритм предусматривает последовательность контроля признаков 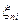в порядке, определенном R₁.

Если 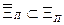, то определяется разность 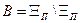, и выбирается подмножество 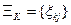, 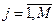косвенных признаков. При этом мощность множества 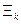должна быть такой, чтобы по возможности полностью компенсировать неоцениваемые прямые признаки.

Подмножество косвенных признаков 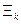полностью упорядочивается введением отношения порядка R₂ в предположении 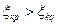, если 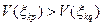. В качестве критерия 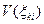, который определяется на элементах 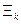, можно использовать норму вектора чувствительности 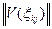, где

;

.

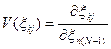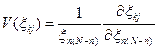При упорядочении в соответствии с R₂ необходимо учитывать, что введенный порядок из-за возможного изменения прямых признаков 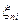с течением времени нарушается. Поэтому после введения порядка целесообразно установить пределы изменения признаков 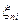, при которых отношение порядка R₂ не будет нарушаться.

Упорядоченное множество косвенных признаков полностью определяет алгоритм диагностирования, обуславливающий измерения косвенных признаков в соответствии с порядком R₂. Из множества 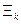выбираются диагностические признаки, которые можно измерить, т.е. ; .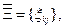

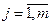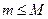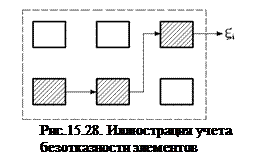
Методическая составляющая достоверности определения состояния ЭО при контроле выбранных совокупностей прямых и косвенных диагностических признаков устанавливается по величине вероятности р(n,m) и вычисляется следующим образом:

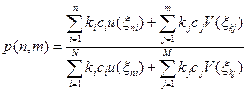, (15.6)

где n и m числа измеряемых соответственно прямых и косвенных диагностических признаков; k_i,k_j – коэффициенты, учитывающие безотказность основных частей объекта, участвующих в формировании данного признака (прямого и косвенного) (рис.15.28); коэффициенты k_i, k_j могут быть взяты у объекта-аналога или рассчитаны; если такового нет, то принимается k_i = k_j = 1; c_i,c_j – коэффициенты, учитывающие важность признаков 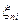, , 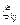рассчитываются методами экспертных оценок. Если такая оценка отсутствует, то принимается c_i = c_j = 1; 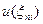, 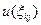– ранги, отражающие объективную оценку признака, могут рассчитываться как чувствительности изменения состояния объекта к изменению рассматриваемого диагностического признака.

При необходимости обеспечить вероятность р(n,m), равную единице нужно, чтобы выполнялось условие n = N, т.е. следует измерять все прямые признаки. Если задана достоверность оценки состояния ЭО через вероятность Р_о<1, то n и m выбираются с учетом

введенных порядков R₁ и R₂ так, чтобы обеспечить р(n,m) 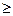р_о.

Если условиене выполняется, то пересматриваются совокупност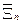и и 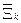, чтобы обеспечить требуемую достоверность оценки состояния ЭУ.

После того, как сформированы совокупност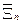и и 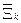, определяются условия работоспособности (УР) как области допустимых изменений измеряемых признаков оборудования и признаки дефектов (ПД).

Условие работоспособности ЭУ определяется, исходя из основных требований, предъявленных к ЭУ при его использовании по прямому назначению. УР формируется в области признаков функционирования ЭУ, а затем трансформируется в область работоспособности в пространстве оцениваемых диагностических признаков. Таким же образом определяются признаки наличия дефектов в объекте. В отличие от УР признаки наличия в объекте дефекта не всегда определяют работоспособность объекта.

После этого выбираются методы измерения прямых М_пi и косвенных М_кi диагностических признаков. Каждый из выбранных для оценки в процессе диагностирования диагностический признак может оцениваться различным методом. В связи с этим разработчику диагностического обеспечения необходимо выбрать конкретный метод М_i(j) для оценивания каждого 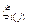. Выбор метода основывается на требуемой точности оценки и учитывает условия, в которых выполняется диагностирование.

При этом необязательно, чтобы все диагностические признаки ЭУ оценивались идентичными методами.

В конце процедуры строятся алгоритмы А диагностирования ЭУ. Алгоритм диагностирования оборудования предусматривает последовательное выполнение определенного числа проверок, связанных с оценкой диагностических признаков и анализом получаемых результатов.

В результате реализации процедуры, приведенной на рис.15.27, разработчики СД получают перечень оцениваемых диагностических признаков, условия работоспособности и признаки дефектов, методы их оценки, а также алгоритмы диагностирования.

В процессе реализации процедуры разработчики объекта поддерживают тесную связь с проектировщиками средств диагностирования и деятельности человека-оператора, что позволяет принять согласованные решения и внести соответствующие корректировки. Так, после выбора оцениваемых диагностических признаков и методов их оценки необходимо определить возможность технической реализации выбранных методов в заданных условиях эксплуатации ЭУ при наличии соответствующей материальной базы и определенной квалификации обслуживающего персонала. Формулировка УР и ПД задает требования по точности оценки диагностических признаков, которые должны быть согласованы с разработчиками средств диагностирования.

Алгоритмы диагностирования связаны с уровнем автоматизации процесса оценки состояния оборудования и определяют требования по организации деятельности ЧО. При разработке алгоритмов диагностирования важное значение имеет оценка их по выбранным критериям для определения требуемой эффективности диагностирования.

Анализ ДМ может быть выполнен различными методами с использованием разнообразного математического аппарата. Все методы анализа разделяются на аналитические, графические и графоаналитические.

Аналитические методы в ходе анализа позволяют применить способы оптимизации и получить соотношения, характеризующие ЭУ при изменении его состояния. К аналитическим методам анализа ДМ относятся методы малого параметра, теории чувствительности, планирования эксперимента, распознавания образов, математической логики. Методы и аппарат математической логики (двузначной и многозначной) часто используются для анализа дискретных моделей с целью структурного моделирования диагностируемого оборудования. С помощью аппарата математической логики может осуществляться анализ специальных ДМ, характеризуемых конечным числом состояний. Аналитические методы достаточно эффективны при анализе любой ДМ, однако с возрастанием сложности модели решение становится слишком громоздким и требуется привлечение ЭВМ.

Графические методы обладают большой наглядностью и могут служить как для непосредственного анализа, так и для иллюстрации аналитических методов. Они весьма полезны для исследования быстропротекающих процессов или характеристик оборудования. Среди графических методов особое место занимают методы, основанные на теории ориентированных или неориентированных графов. При исследовании структурных свойств графов часто оказывается удобным использовать матричные представления.

Графоаналитические методы представляют собой разнообразные комбинации графических и аналитических методов анализа.

При выполнении анализа непрерывных моделей, представленных линейными алгебраическими и дифференциальными уравнениями, а также при использовании теории графов широко применяется матричный аппарат. Это позволяет представить решение и исследовать систему уравнений в удобной лаконичной форме, а кроме того облегчается процедура построения алгоритмов для реализации процессов на ЭВМ.

Примеры анализа диагностических моделей

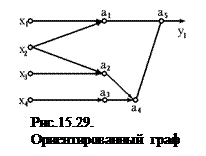
Пример 1. ДМ в виде ориентированного графа. Если ОД представлен специальной ДМ в виде ориентированного графа, то решить задачу выбора совокупности оцениваемых диагностических параметров можно следующим образом.

Ранжировать вершины графа (диагностические параметры) по правилу: всем вершинам, имеющим в качестве входов только множества х₁,...,х_n, присваивается ранг 1; затем любой вершине, имеющей в качестве входов входы из множества х₁,...,х_n, и выходы вершин с рангом 1, присваивается ранг 2 и т.д.

Для ориентированного графа (рис.15.29) рангами вершин будут: u(а₁) = u(а₂) = u(а₃) = 1; u(а₄) = 2; u(а₅) = 3.

Пусть для простоты k_i = 1, c_i = 1, 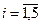(15.6) и необходимо обеспечить методическую составляющую достоверности Р₀ 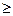0.9.

Рассчитаем р(n) при исключении одного из параметров с рангом 1. Получим р(а₅,а₄,а₃,а₂) = 7/8 = 0,88 < Р_о.

Следовательно, для ОД исключить из рассмотрения хотя бы один параметр невозможно. Для обеспечения заданной достоверности необходимо оценивать все диагностические параметры

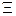= (а₁,а₂,а₃,а₄,а₅).

Развитие этого подхода предполагает введение весовых коэффициентов для вершин с учетом стоимости, времени измерения и т.д.

Пример 2. Информационная ДМ. Решить задачу упорядочения диагностических параметров можно используя информационный критерий вида:

I_j = I_бj + I_сj,

где I_бj – составляющая, учитывающая свойства j-го параметра через безотказность элементов; I_сj – составляющая, учитывающая структурные свойства j-го параметра.

Рассмотрим каждую составляющую отдельно.

Первую составляющую можно определить через показатель надежности элементов объекта, состояние которых определяется через j-й параметр

,

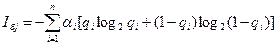где 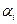– коэффициенты значимости (вес) i-го элемента, формирующего j-й параметр, 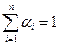; q_i –вероятность отказа i-го элемента, формирующего

j-й параметр,(q_i = 1-р_i,где р_i – вероятность безотказной работы i-го элемента за рассматриваемый интервал времени); n – число элементов объекта, изменение состояния которых чувствуется j-м параметром.

Это можно пояснить на следующем примере (рис. 15.30).

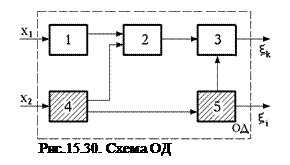Параметр 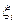чувствителен только к изменению состояния 4-го и 5-го элементов при условии подачи на вход ОД нормальных входных сигналов х₁ и х₂.

В качестве величины 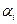, характеризующей значимость i-го элемента, можно использовать выражение:

,

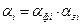где 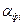– функциональная значимость i-го элемента; 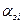– значимость по затратам на изготовление и восстановление состояния i-го элемента.

Определить 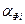можно, воспользовавшись матрицей связанности вида

	s1	s2	...	sn
s1	1	0		1
s2	0	1		1
...
sn	0	1		1

Число строк равно числу столбцов, которое определяется числом СЕ, элементов ОД. Таблица заполняется по правилу: если i-й элемент связан с k-м элементом, то ставится 1, в противном случае – 0.

Ранг R_i определяется как сумма всех единиц в i-й строке. С учетом величины R_i определяется коэффициент функциональной значимости:

.

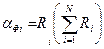Коэффициент значимости, учитывающий затраты 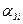, определяется как

,

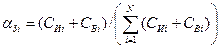где С_иi – стоимость изготовления и установки в объект i-го элемента; С_вi – стоимость восстановления i-го элемента (одного или за определенный интервал времени).

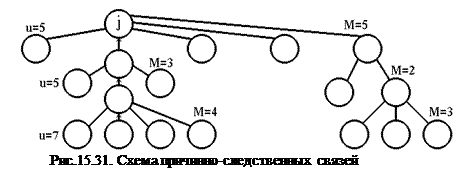
Вторая составляющая критерия I_j может быть определена, если построена схема причинно-следственных связей между j-м диагностическим параметром и элементами объекта, к изменению состояния которых чувствителен этот параметр (рис.15.31).

Ограничения такой структуры заключаются в том, что элементы одного уровня не связаны друг с другом, а элемент любого n-го уровня не должен быть связан более чем с одним элементом вышестоящего уровня .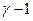

Такие допущения при эксплуатации не всегда правомерны, однако для инженерной практики вполне допустимы при выполнении приближенных расчетов. В противном случае используемый критерий для практических расчетов не пригоден.

С учетом указанных ограничений критерий Iсj может быть определен по формуле:

,

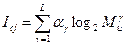где 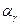– значимость 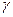-го уровня элементов в формировании j-го диагностического параметра; L – число условных уровней формирования диагностического параметра; 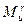– число элементов на 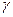-м уровне, характеризующих состояние u-го элемента на 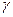-1-уровне.

Сравнивать параметры 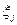можно по абсолютным значениям информационного критерия 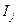или по нормированным величинам

,

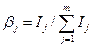где m – число рассматриваемых параметров.

В результате получается ряд вида I_j>I_m>...>I_i или 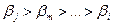, что позволяет ранжировать рассматриваемые параметры .

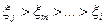Анализ полученных рядов позволяет выбирать наиболее информативные диагностические параметры, исключив неинформативные. Тем самым сокращается число параметров, подлежащих контролю.