Сведения о марковских процессах

Марковским процессом называется случайный процесс Х(t), который обладает следующим свойством: если в момент t_о известно значение Х(t_о), то вероятностная оценка течения процесса в будущем не зависит от того, как протекал процесс до момента t_о.

Для любых двух моментов t₁ и t₂ (t₁<t₂) условие вероятности

Р[x(t₂)=j, [x(t₁)=i] = p_ij(t₁,t₂)

называют переходными вероятностями.

Если p_ij(t₁,t₂) зависят лишь от t₂-t₁ = t так, что p_ij(t₁,t₂) = p_ij(t),

то марковский процесс называется однородным.

Функция p_ij(t) характеризует вероятность перехода из состояния i в начальный момент в состояние j в конечный момент промежутка времени t и удовлетворяет условию

,

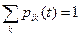что означает неизбежность перехода за отрезок времени t из состояния i в состояние j.

В том случае, когда параметр t принимает лишь дискретную последовательность значений, например, целых неотрицательных чисел t = 0, 1, 2,...,n, марковские случайные процессы называют процессами с дискретным временем, или марковскими цепями. Однородные марковские цепи описываются заданием вероятности p_ik перехода из состояния i в состояние k за одно испытание.

Марковскую цепь можно представить в виде матрицы переходных вероятностей. Например, для случая трех состояний матрица имеет вид

.

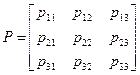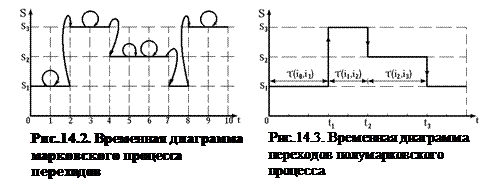Эту цепь можно представить как временной процесс перехода из состояния в состояние следующим образом (рис.14.2). Допустим, что объект находится в трех состояниях s₁,s₂,s₃. В момент t = 0 – в состоянии s₁. Через каждую единицу времени t = 1,2,... происходит скачок в состояние, причем объект может перейти в одно из возможных состояний: с вероятностью р₁₂ в s₂, с вероятностью р₁₃ в s₃ и с вероятностью р₁₁ = 1-р₁₂-р₁₃ возвратиться в s₁. На рис. 14.2 в момент t = 1 совершается скачок s₁-s₁, в момент t = 2 скачок s1-s₃, в момент t = 3 – скачок s₃-s₃ и т.д.

Временной процесс перехода из состояния в состояние можно представить несколько отличным от рассмотренного вида (рис.14.3). В этом случае в момент t = 0 объект находится в состоянии s₁. При этом в соответствии с матрицей переходных вероятностей Р = [p_ij] определяется то состояние, в которое объект должен перейти из состояния s₁ (исключается из рассмотрения переход s_i-s_i). После этого берется одна реализация случайного времени пребывания объекта в состоянии s₁,т.е. 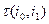, имеющего функцию распределения F_ij(t). Процесс (объект) в течение времени 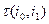пребывает в состоянии s₁, после чего переходит в состояние s₃. В дальнейшем в соответствии с матрицей переходных вероятностей определяют состояние s₂, в которое объект переходит из s₃, время пребывания в состоянии s₃ и т.д.

Семейство функций распределения F_ij(t) для случайных величин 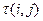представляется в виде матрицы F = [F_ij]. Существенным является то, что выбор времени 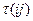на каждом шаге не зависит от характера протекания процесса до момента перехода объекта в состояние s_i. Рассмотренный случайный процесс, в отличие от однородного марковского процесса, называется полумарковским.

Полумарковский процесс можно определить заданием одной матрицы Q (вместо двух матриц P и F):

Q = [q_ij(t)], q_ij(t) = P_ijF_ij(t).

Величина q_ij(t) выражает вероятность события, при котором в исходном состоянии s_i процесс перейдет за один шаг в состояние s_j, причем время пребывания в состоянии s_i не превысит величину t. Например, случайный процесс характеризуется матрицей переходных вероятностей Р и матрицей функции распределения F:

. .

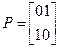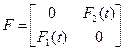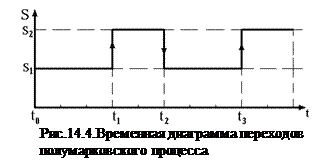
У такого процесса смена состояний происходит детерминировано: 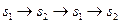. Во времени процесс может быть представлен следующим образом (рис.14.4).

В интервале t_о–t₁ объект находится в состоянии s₁. В момент t₁ объект переходит в состояние s₂. В этом состоянии объект находится в течение времени t₁–.t₂, а в момент t₂ переходит опять в состояние s₁, в котором находится в период t₂–.t₃. Интервалы времени нахождения в состояниях s₁ и s₂ независимы. Функция распределения времени

нахождения в состоянии s₁ есть F₁(t), а в состоянии s₂ – F₂(t).