Методы построения алгоритмов поиска дефектов

Метод, основанный на показателях надежности СЕ. Строить алгоритм поиска дефектов можно на основе известных показателей надежности, в качестве которых используются показатели безотказности (вероятности отказа q_i или безотказной работы р_i) и ремонтопригодности (время, затрачиваемое на обнаружение дефекта ). Возможны три способа:

по показателям безотказности;

по показателям ремонтопригодности;

по отношению /q_i (время - вероятность).

Для построения алгоритмов поиска дефектов необходимо знать показатели q_i, для каждой СЕ объекта, .

1. Последовательность выполнения проверок, т.е. алгоритм поиска дефекта может быть построен на основании известных значений вероятности отказа qi структурных единиц.

При построении алгоритма поиска дефекта вводятся допущения: длительности всех проверок равны;

отказы СЕ независимы;

одновременно отказывает только одна (любая) СЕ.

В этом случае алгоритм поиска может быть последовательным. Для его реализации структурные единицы объекта, для которых заданы вероятности отказа q_i, упорядочиваются по величине, и последовательно выполняются проверки, начиная с СЕ, характеризуемой наибольшей величиной q_i, и заканчивая СЕ, характеризуемой наименьшей.

Пример.Для ОД, состоящего из четырех СЕ известны, вероятности отказа каждой q_i: q₁ = 0.6; q₂ = 0.1; q₃ = 0.18; q₄ = 0.12. Ранжируем СЕ по q_i. Получаем: q₁,q₃,q₄,q₂. Этот порядок определяет структуру алгоритма поиска дефектов (рис.8.7).

2. Если имеется информация о времени, затрачиваемом на поиск дефектов каждой СЕ, то можно построить алгоритм поиска по правилу: проверку начинать с СЕ, на поиск дефекта которой затрачивается наименьшее время. Зная значения , можно расположить их в ряд в порядке возрастания и построить алгоритм поиска.

Пример. Для ОД, состоящего из трех СЕ, известно время : t_п1 = 0.4ч; t_п2 = 0.14ч; t_п3 = 0.2ч.

Алгоритм поиска дефектов имеет вид, показанный на рис.8.8.

3. Метод "Время - вероятность" является наиболее совершенным, т.к. учитывает два показателя. В этом случае последовательность проверок должна удовлетворять условию, согласно которому номер проверки определяет отношение /q_i и возрастает с увеличением отношения.

Пример. В ОД из пяти СЕ имеется дефект. Известно: q_i: q₁ = 0.05; q₂ = 0.15; q₃ = 0.30; q₄ = q₅ = 0.25;

t_пi: t_п1 = 1 ч, t_п2 = 2 ч, t_п3 = 3 ч, t_п4 = 4 ч, t_п5 = 4.5 ч.

Необходимо построить алгоритм поиска дефектов.

Составим отношения /q_i: t_п1/q₁ = 20, t_п2/q₂ = 13,3, t_п3/q₃ = 10, t_п4/q₄ = 16, t_п5/q₅ = 18.

Алгоритм поиска представлен на рис.8.9.

Неопределенность в проверке может быть снята предпочтением показателям ремонтопригодности или безотказности.

Рассмотренные методы не позволяют учесть взаимосвязи между СЕ, т.е. структуру ОД.

Информационный метод. Предполагается, что отказы всех СЕ, соединенных последовательно, равновероятны и образуют полную группу событий:

q₁ = q₂ =...= q_n = 1/n,

где n – число возможных состояний (дефектов).

Каждая проверка имеет два исхода: 1 и 0.

Перед началом поиска состояние ОД характеризуется максимальной энтропией (мерой неопределенности)

.

Каждая проверка дает определенное количество информации о состоянии объекта

,

где – средняя условная энтропия состояния объекта при выполнении проверки .

Поскольку для проверки возможны только два исхода (1 и 0) с вероятностями р( ) и р( ) соответственно, то

,

где и энтропии состояния объекта после проведения проверки ; l – число обнаруживаемых проверкой состояний.

Тогда и количество информации

.

При построении алгоритма первой проверки выбирается , несущая максимум информации (если таких проверок больше одной, то выбирается любая из них), т.е.

.

Второй выбирается проверка , которая обладает наибольшей условной информацией относительно состояния, характеризуемого энтропией ,

где l₁ – число обнаруживаемых состояний; l₂ – число необнаруживаемых состояний.

Для этого случая

.

Третья и последующие проверки выбираются аналогичным образом. Процедура заканчивается тогда, когда энтропия станет равна нулю.

Недостаток информационного метода заключается в том, что он может быть использован только для ОД, схемы которого сводятся к последовательному соединению элементов, вероятности отказов которых равны.

Пример. Построить алгоритм поиска дефекта, используя информационный алгоритм для объекта, схема которого представлена на рис.8.10.

Составим таблицу состояний. В последнем столбце табл.8.2 приведены значения для каждой проверки. Анализируя таблицу, приходим к выводу, что проверка не несет дополнительной информации и ее можно исключить из дальнейшего рассмотрения. Наибольшее количество информации дают проверки и . Выбираем в качестве первой проверки в алгоритме поиска проверку и переписываем табл.8.2 в следующем виде (табл.8.3). Действуя в соответствии с предложенной методикой, второй проверкой выбираем и составляем следующую табл.8.4. В результате анализа табл.8.4 выбираем и составляем табл.8.5.

Таким образом, алгоритм поиска дефекта будет включать три проверки, выполненные в следующей последовательности , , .

Простейшим примером метода является алгоритм половинного разбиения, при котором любая проверка снимает половину неопределенности .

Если признаки наличия дефектов не дают основания считать какой-либо элемент дефектным, то целесообразно выполнить первую проверку в контрольной точке, находящейся в середине схемы. Если результат проверки указывает на то, что сигнал в этой точке имеет допустимые значения, то из дальнейшего рассмотрения исключается первая половина схемы. Если в этой точке зафиксирован отрицательный результат, то дефект необходимо искать в первой половине схемы с последовательным соединением элементов. Процесс деления схемы пополам следует повторять до тех пор, пока не будет обнаружен последний дефект. Для ОД, состоящего из четырех элементов, (рис.8.11,а), алгоритм поиска дефекта, реализующий метод половинного разбиения, приведен на рис.8.11,б.

Таблица 8.2

Таблица состояний

	si
s1	s2	s3	s4	s5
						0.72
						0.972
						0.72
						0.972
						-

Таблица 8.3

Первая преобразованная таблица состояний

	si
s1	s2	s3	s4	s5
						-
						0.548
						0.548
						0.548

Таблица 8.4

Вторая преобразованная таблица состояний

	si
s1	s2	s3	s4	s5
						0.746
						0.314
						0.264

Таблица 8.5

Третья преобразованная таблица состояний

	si
s1	s2	s3	s4	s5

Метод,основанный на анализе чувствительностей функций передачи. Если диагностическая модель ОД задана в виде диаграммы прохождения сигналов (ориентированного графа) вида (рис.8.12), то можно определить чувствительность функций передачи к изменению состояний элементов по формуле

или ,

где T_ij – функция передачи от i-го узла к j-му узлу; – изменяющиеся параметры, .

Вершины диаграммы соответствуют переменным и обозначаются индексом соответствующего сигнала. Ветви имеют операторы, обозначенные соответствующей зависимостью с указанием направления. Расположение вершин должно отражать распространение сигналов в объекте.

Простой пример диаграммы прохождения сигналов проиллюстрируем на делителе напряжения (рис.8.13,а). Диаграмма приведена на рис.8.13,б.

В общем случае сигнал 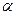-й вершины определяются следующим образом:

,

т.е. сумма произведений сигналов, входящих в узел, на соответствующие функции передачи.

В реальном объекте функции передачи зависят от структуры объекта и значений их параметров. Все изменения (количественные и качественные), происходящие в объекте, приводят к изменению соответствующих функций передач. В связи с этим различная чувствительность параметров определяется чувствительностью функций передач, которая находится как степень ее изменения при изменении какого-либо параметра.

Обычно ОД характеризуется множеством функций передач. Их число определяется как сочетания

,

где n – число параметров ОД (если все параметры изменяются, то n = l).

Сравнивая чувствительности, нужно упорядочить диагностические параметры по их чувствительности к изменению состояния объекта, что составит алгоритм поиска дефектов. Анализ облегчится, если воспользоваться таблицей чувствительностей функций передач (табл.8.6). Каждый столбец этой таблицы представляет чувствительности функций передач к изменениям одного и того же параметра каждая строка – чувствительности одной функции передачи к изменению параметров.

Для выбора последовательности проверок, составляющих алгоритм поиска дефектов, анализ таблицы сводится к сравнению строк. При этом осуществляется ранжирование вида

, если ,

где функция передачи T_oi является наилучшей.

Далее анализируются строки с целью определения параметров, к которым функции передачи наиболее чувствительны. А эти параметры зависят от физических элементов, дефекты которых могут привести к их изменению. Упорядоченный ряд параметров по степени влияния на функции передачи ОД определяет алгоритм поиска дефектов.

Обнаружить возникшие дефекты можно с помощью как рабочих, так и специальных тестовых сигналов.

Метод, основанный на анализе таблиц состояний. Поиск дефекта в этом случае базируется на минимальной совокупности проверок, позволяющих различить дефекты всех СЕ. Рассмотрим метод на примере ОД, представленного на рис.8.14.

Считаем, что дефект каждой СЕ нарушает работоспособность ОД. Тогда множество неработоспособных состояний S_н будет включать пять элементов, т.е. S_н={s_i}, , где s_i – состояние неработоспособной СЕ.

Обнаружить все дефекты в таком ОД можно, выполнив пять проверок, т.е. , . При этом считаем, что каждая проверка может иметь два результата: 0 – СЕ неработоспособна, 1 – СЕ работоспособна.

Можно ли сократить число проверок ?

Составим таблицу состояний в виде табл.8.7.

Как видно, проверка не несет информации (все 0). Действительно, если известно, что ОД отказал, то проверка на его выходе не даст новой информации по поиску дефекта.

Составим табл.8.8 попарного сравнения всех состояний ОД для оценки различимости пар состояний той или иной проверкой. Если состояния различаются проверкой, то – 1, если не различаются, то 0.

Анализ табл.8.8 показывает, что проверка различает четыре пары состояний; проверка – еще четыре пары состояний; проверка – дополнительно лишь одну пару, а проверка – дополнительно две пары состояний. Исключив как наименее информативную, включим в алгоритм три проверки.

Метод распознавания образов. В зависимости от требуемой глубины поиска дефектов множество состояний ОД, заданного схемой соединений, можно разбить на конечное число классов.

При этом совокупность свойств, позволяющих отнести ряд состояний к одному классу, составляет образ, а задача поиска дефектов сводится к распознаванию образов.

Для решения задачи необходимо:

определить совокупность диагностических параметров , ;

построить образы отказавших СЕ, блоков, до которых требуется отыскивать дефект в ОД.

Рассмотрим содержание этих этапов.

1. С учетом заданной глубины поиска дефекта путем физического или математического моделирования формируется таблица неработоспособных состояний. В качестве диагностической модели могут использоваться дифференциальные или алгебраические уравнения. После введения дефекта в каждую СЕ (блок), приводящую к ее отказу и отказу ОД, измеряются значения параметров с помощью датчиков, установленных в соответствующих контрольных точках. Результаты эксперимента сводятся в табл.8.9, число строк которой равно числу возможных дефектов в ОД S= {s_i}, , а число столбцов – множеству значений измеряемых параметров .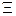

На пересечении j-го столбца и i-й строки записывается значение параметра при отказе i-й СЕ, т.е. состояний объекта S_i.

Из рассматриваемой совокупности параметров 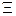необходимо выделить наиболее информативные, значительно изменяющиеся при возникновении отказов, доступные измерению, однозначно соответствующие тому или иному отказу. В этом случае, если последнее условие не выполняется, задачу поиска дефекта необходимо решить по результатам измерения нескольких параметров.

Совокупность диагностических параметров на основании таблицы неработоспособных состояний можно выбрать, воспользовавшись принципом разрешающей способности параметров, по формуле:

,

где , , значение порога чувствительности технического средства диагностирования электроустановки.

2. Для выбранной совокупности диагностических параметров имеем ряд чисел из множества . Совокупность этих чисел можно интерпретировать геометрически как точку в многомерном пространстве диагностических параметров. По осям координат этого пространства откладываются в абсолютных или относительных единицах значения параметров. В результате в пространстве параметров появится множество точек А₁,А₂,...,А_n, характеризующих состояние ОД с соответствующими отказавшими блоками. Область значений параметров, соответствующих работоспособному состоянию, обозначим через R (рис.8.15).

Области, соответствующие одновременно дефектам в двух или более блоках, свидетельствуют о трудно различимых отказах.

Распознавание дефекта в этом случае сводится к определению расстояния между точкой В, соответствующей текущему состоянию ОД, и всеми точками А_i. Искомое изображение относится к тому образу, расстояние до которого минимально, т.е.

, если d(B,A_i)=min d(B,A_i).

Это расстояние вычисляется по формуле, определяющей меру сходства В и А_i.

,

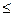где j – число рассматриваемых диагностических параметров; – число образов, m n. В результате процедуры распознавания осуществляется поиск дефекта СЕ (блока), приведшего к отказу объекта диагностирования.

Пример. В качестве ОД рассматривается система возбуждения генератора (рис.8.16), включающая турбогенератор ТГ, линейный дроссель ЛД, блок коррекции напряжения БКН, трансформатор фазового компаундирования ТФК, магнитный усилитель МУ, дроссель отсоса ДО, выпрямитель В.

В качестве параметров, характеризующих работу схемы, будем рассматривать: напряжение статора генератора U_г; ток в обмотке линейного дросселя I_д; ток трансформатора фазового компаундирования I_т; рабочий ток дросселя отсоса I_o; суммарный ток системы компаундирования I_k; ток возбуждения синхронного генератора I_в.

В результате моделирования дефекта была составлена таблица неработоспособных состояний, анализ которой позволил в качестве диагностических параметров выбрать U_г и I_o.

Для указанных параметров геометрическая иллюстрация образов дефектов имеет вид, показанный на рис.8.17.

Приведенные области изменения параметров А₁...А₇ являются образами отказов блоков системы возбуждения генератора: S_в – выпрямителя, S_м - магнитного усилителя, S_б – блока коррекции напряжения, S_o – дросселя отсоса, S_д – линейного дросселя, S_т – трансформатора.

Для определения отказавшего блока необходимо измерить параметры U_г и I_o и найти в пространстве точку, характеризующую текущее состояние системы возбуждения. Определив минимальное расстояние из всех возможных, находим отказавший блок. Например, если U_г>1.53 и рабочий ток дросселя отсоса I_o = 0, то отказал дроссель отсоса, дефект – обрыв обмотки управления дросселя.

Контрольные вопросы

1. Что нужно сделать, чтобы составить таблицу дефектов?

Ответы:

а) выполнить моделирование дефектов и испытания;

б) провести анализ диагностической модели и испытания;

в) выполнить моделирование дефектов или анализ диагностической модели.

2. Как представить алгоритм поиска дефектов в виде графа?

Ответы:

а) вершины – элементы, ветви - проверки;

б) вершины – проверки, ветви – направления движения по результатам проверки;

в)вершины – проверки, ветви – обнаруживаемые дефекты.

3. Назовите основные свойства последовательного алгоритма поиска дефектов.

Ответы:

а) последовательное выполнение проверок;

б) обнаружение каждой проверкой одного дефекта;

в) последовательное разбиение ОД на равные части.

4. Что необходимо иметь для построения алгоритма поиска дефектов методом "время-вероятность"?

Ответы:

а) время поиска каждого дефекта, вероятности отказов;

б) функциональная схема, время поиска каждого дефекта и вероятность безотказной работы;

в) функциональная схема и вероятность безотказной работы;

5. Как определяется мера неопределенности состояния ОД?

Ответы:

а) ;

б) ;

в) .

6. Почему алгоритм половинного деления является разновидностью информационного алгоритма поиска дефектов?

Ответы:

а) используется информация о количестве элементов ОД;

б) используется информация об очередности выполнения проверок;

в) используется информация, получаемая каждой проверкой.

7. Укажите последовательность действий при анализе таблицы чувствительностей функций передачи для построения алгоритма поиска дефектов.

Ответы:

а) ранжирование строк по чувствительности, ранжирование параметров, к которым функция передачи параметров наиболее чувствительна;

б) ранжирование параметров по чувствительностям к ним функций передач;

в) ранжирование параметров по чувствительностям к ним функций передач, ранжирование функций передач к выбранным параметрам.

8. Как можно сократить число проверок для обнаружения всех дефектов при анализе таблицы состояний?

Ответы:

а) заполнить таблицу по правилу "проверка обнаруживает дефект – 0, не обнаруживает – 1" и исключить наименее информативную проверку;

б) заполнить таблицу попарного сравнения проверок по правилу "различают дефект – 1, не различают – 0" и выбрать наиболее информативную;

в) то и другое.

9. Определите правильную последовательность действий при использовании метода распознавания образа.

Ответы:

а) составить таблицу неработоспособных состояний по результатам моделирования дефектов; построить образы дефектов в координатах рассматриваемых параметров; определить расстояние между текущим состоянием и образом; установить диагноз;

б) выбрать совокупность диагностических параметров; составить образы рассматриваемых дефектов; определить расстояние от текущего состояния до образов; установить диагноз;

в) составить таблицу неработоспособных состояний по результатам моделирования дефектов; выбрать совокупность диагностических параметров - построить образы в координатах диагностических параметров; определить расстояние до образов дефектов; установить диагноз.

ГЛАВА 9