Общие понятия об остойчивости
УДК 629.5:532.3.073
К36
Под редакцией д.т.н., проф. Е.П. Роннова
Кеслер, А.А. Теория и устройство судна. Ч.2. Основы остойчивости: / учеб. пособие / А.А. Кеслер. – Н. Новгород : Изд-во ФБОУ ВПО «ВГАВТ», 2013. – …с.
Изложены теоретические основы метода начальной остойчивости и метода остойчивости при больших углах наклонения. Представлены возможности применения метода начальной остойчивости для решения прикладных задач.
Для студентов очного и заочного обучения специальностей 180403.65 «Судовождение», 180405.65 «Эксплуатация судовых энергетических установок», 180407.65 «Эксплуатация судового электрооборудования и средств автоматики».
Объем материала пособия отвечает требованиям к уровню знаний по гидростатике судна, которые предъявляются к студентам указанных специальностей.
Работа рекомендована к изданию кафедрой проектирования и технологии постройки судов (протокол № 10 от 26.06.13 г.)
Ó ФБОУ ВПО «ВГАВТ», 2013
Начальная остойчивость
Малые равнообъемные наклонения
Теорема Эйлера
Одним из двух положений (допущений) метода начальной остойчивости является теорема Эйлера о равнообъемных ватерлиниях.
Теорема гласит, что линия пересечения равнообъемных ватерлиний при бесконечно малом угле наклонения проходит через центры тяжести площадей начальной и конечной ватерлиний.
Для доказательства этой теоремы рассмотрим наклонение судна вокруг продольной оси на правый борт (рис. 2.1). На рис. 2.1 принято: наклонение судна происходит на бесконечно малый угол (dq) при сохранении прямостенности корпуса; ВЛ0, ВЛ1 – след начальной и конечной (после наклонения) ватерлиний соответственно; dV1, dV2 – объем клина водоизмещения вошедшего в воду и вышедшего из воды соответственно. Из условия равнообъемного наклонения имеем dV1 = dV2.
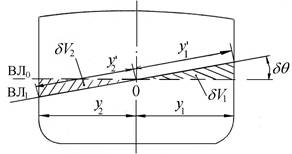 |
Рис. 2.1. К доказательству теоремы Эйлера
Предположим, что следы плоскостей начальной и конечной ватерлинии пересекаются в точке 0. С учетом того, что угол наклонения бесконечно мал, тангенс угла и его значение в радианах можно принять равными.
Приняв во внимание начальную ватерлинию ВЛ0, объем клина, вошедшего в воду по всей длине корпуса (от – L/2 до + L/2), можно представить в виде
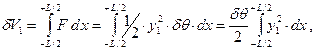 |
| где | 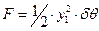 | – | площадь сечения клина; |
| dx | – | элемент длины корпуса судна; | |
| dq | – | постоянный по длине корпуса угол. |
Аналогично можно получить выражение для вышедшего из воды клина водоизмещения
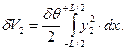 | (2.1) |
Из равенства объемов клиньев, вошедшего и вышедшего из воды, получаем следующее условие равнообъемного наклонения
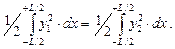 |
Правая и левая части этого равенства представляют собой статический момент части площади ватерлинии, расположенной по одну сторону от оси «х», поскольку 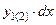 есть элементарная площадка, а
есть элементарная площадка, а 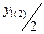 – расстояние от центра ее тяжести до оси «х» (рис. 2.2).
– расстояние от центра ее тяжести до оси «х» (рис. 2.2).
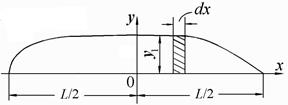 |
Рис. 2.2. К определению статического момента площади ватерлинии
Статические моменты двух частей площади любой фигуры относительно оси, разбивающей фигуру на эти части, равны только тогда, когда ось проходит через центр тяжести площади фигуры. Поскольку статические моменты двух частей площади начальной ватерлинии равны, то ось, относительно которой они взяты, проходит через центр тяжести площади начальной ватерлинии. Повторив эти рассуждения для ВЛ1 можно получить такой же вывод и для конечной ватерлинии.
Таким образом, линия пересечения двух равнообъемных ватерлиний при бесконечно малом наклонении проходит через центры тяжести обеих ватерлиний. Теорему Эйлера распространяют и на конечные, но малые углы наклонения. На практике к малым углам наклонения относят углы до 7–10°. Теорема Эйлера выполняется при наклонениях в пределах прямостенности бортов (рис. 2.1).
Углы наклонения судов в продольной вертикальной плоскости (углы дифферента), как правило, не превышают 7°. При продольном наклонении след конечной ватерлинии будет пересекаться со следом начальной ватерлинии в точке F – в центре тяжести начальной ватерлинии (рис. 2.3).
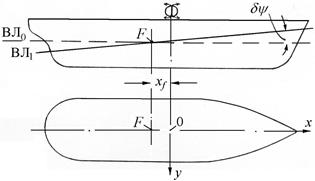 |
Рис. 2.3. Положение равнообъемных ватерлиний при дифференте
Поперечная ось, проходящая через точку F, в этом случае будет осью вращения судна.
При перемещении груза
Изменение посадки и остойчивости при перемещении грузов удобно рассматривать, разделяя общий процесс переноса груза из одной произвольной точки на судне в другую на три последовательных переноса: в вертикальном, поперечном и продольном направлениях. В результате такого перемещения груза посадка и остойчивость судна будут такими же, как и после единовременного переноса из исходной точки в конечную по прямой.
Вертикальное перемещение груза. Плечо такого перемещения можно определить, зная аппликату центра тяжести груза в начальном и конечном положениях (рис. 2.9).
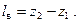
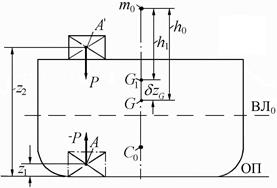 |
Рис. 2.9. Вертикальное перемещении груза
Изменение положения груза по высоте вызовет перемещение центра тяжести судна в том же направлении.
Величины перемещений центра тяжести груза и судна будут обратно пропорциональны их весам:
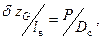 или или 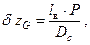 | (2.8) |
| где | 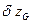 | – | перемещение центра тяжести судна; |
| Р, Dc | – | вес груза и судна соответственно. |
При вертикальном перемещении груза r0, R0 и 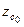 не изменяются, т.к. неизменным остается погруженный объем корпуса. Метацентрические высоты (h0,
не изменяются, т.к. неизменным остается погруженный объем корпуса. Метацентрические высоты (h0, 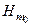 ) изменяются вследствие изменения центра тяжести судна на
) изменяются вследствие изменения центра тяжести судна на 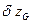 (рис. 2.9).
(рис. 2.9).
Новое значение поперечной метацентрической высоты, с учетом (2.8) можно получить по формуле
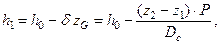
которая применима к перемещению груза по вертикали в любом направлении. В частности при перемещении груза снизу вверх плечо перемещения (z2 – z1) будет иметь положительный знак, соотношение метацентрических высот будет (h0 > h1), а судно станет менее остойчивым.
Аналогично для продольной метацентрической высоты после перемещения груза получаем
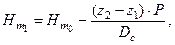
| где | 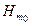 | – | продольная метацентрическая высота до перемещения груза. |
При вертикальном перемещении груза на судне, находящемся в положение прямо и на ровный киль, наклонение не возникает, меняется лишь остойчивость.
При вертикальном перемещении груза изменяются коэффициенты остойчивости:
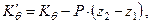 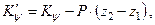 | (2.9) |
| где | 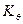 , , 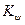 | – | коэффициент поперечной и продольной остойчивости соответственно до перемещения груза. |
Принимая во внимание знак у плеча перемещения (z2 – z1), на основании формул (2.9) можно установить, что при перемещении груза вниз коэффициент остойчивости увеличивается, а при перемещении вверх – уменьшается.
Из формул (2.9) следует, что коэффициенты поперечной и продольной остойчивости при вертикальном перемещении груза изменяются на одну и ту же величину: Р·(z2 – z1).
Вместе с тем, значение коэффициента 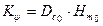 во много раз превышает значение коэффициента
во много раз превышает значение коэффициента 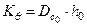 , поэтому вертикальное перемещение груза оказывает более существенное влияние на изменение поперечной остойчивости.
, поэтому вертикальное перемещение груза оказывает более существенное влияние на изменение поперечной остойчивости.
Восстанавливающий момент после перемещения груза может быть представлен в зависимости от коэффициента остойчивости в виде:
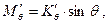
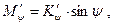
| где | 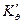 , , 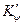 | – | коэффициент поперечной и продольной остойчивости соответственно после перемещения груза по вертикали. |
Перемещение груза по ширине судна.Плечо поперечного перемещения (рис. 2.10) 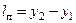 , где у2 и у1 – ординаты центра тяжести груза в конечном и начальном положении соответственно. Ординаты принимаются с плюсом для правого борта и с минусом для левого. После перемещения груза судно накренится на тот борт, в сторону которого перемещается груз, даже если он не перенесен через диаметральную плоскость.
, где у2 и у1 – ординаты центра тяжести груза в конечном и начальном положении соответственно. Ординаты принимаются с плюсом для правого борта и с минусом для левого. После перемещения груза судно накренится на тот борт, в сторону которого перемещается груз, даже если он не перенесен через диаметральную плоскость.
Кренящий момент при перемещении груза определяется как момент сил с плечом 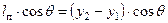 , т.е.
, т.е. 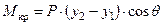 .
.
Приравнивая Мкр восстанавливающему моменту ( 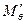 ), определенному с учетом влияния на остойчивость вертикальной составляющей перемещения груза, можно получить
), определенному с учетом влияния на остойчивость вертикальной составляющей перемещения груза, можно получить
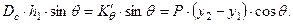 | (2.10) |
Из равенства (2.10) имеем
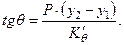
Здесь напомним, что угол крена на правый борт считается положительным (например, рис. 2.10), на левый – отрицательным.
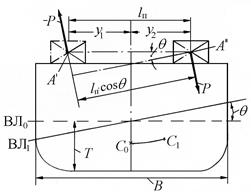 |
Рис. 2.10. Поперечное перемещение груза
Осадку правого (Тпр) и левого (Тл) бортов нетрудно определить по рис. 2.10
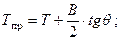
Продольное перемещение груза на судне. Плечо продольного перемещения 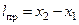 где х1 и х2 – абсцисса центра тяжести груза (рис. 2.11) до и после переноса соответственно с учетом знака.
где х1 и х2 – абсцисса центра тяжести груза (рис. 2.11) до и после переноса соответственно с учетом знака.
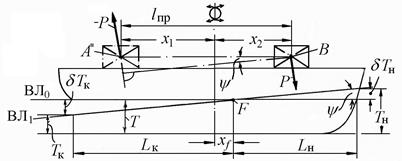 |
Рис. 2.11. Продольное перемещение груза
По аналогии с наклонением судна в поперечной плоскости можно получить выражение для тангенса угла дифферента
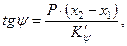
| где | 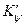 | – | коэффициент продольной остойчивости с учетом вертикальной составляющей перемещения груза. |
Здесь напомним, что угол дифферента на нос (например, рис. 2.11) считается положительным, на корму – отрицательным.
Вследствие продольного наклонения произойдет изменение осадки носом (δТн) и кормой (δТк), которое определяется по формулам, исходя из геометрических построений (рис. 2.11).
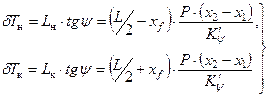 , , | (2.11) |
| где | Lн и Lк | – | отстояние носового и кормового перпендикуляров от оси вращения судна (т. F)*). |
Осадки носом (δТн) и кормой (δТк) с учетом (11) определяются по выражениям
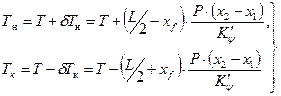 , , | (2.12) |
В формулы (2.12) значения характеристик хf, х2 и х1 вносятся с учетом знака: плюс или минус.
Дифферент судна может быть определен с использованием tgψ или как разность вычисленных осадок, т.е. Δ = L·tgψ = Тн – Тк.
Таким образом, решение задачи о переносе груза из точки «А» с координатами х1, у1, z1 в точку «В» с координатами x2, y2, z2 выполняется в следующей последовательности. Прежде всего определяется изменение остойчивости при вертикальном перемещении груза. Полученные значения 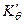 и
и 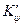 используются для расчета углов наклонения (θ, ψ) и осадок судна (Тпр, Тл, Тн, Тк).
используются для расчета углов наклонения (θ, ψ) и осадок судна (Тпр, Тл, Тн, Тк).
Перемещаемый груз (Р) входит в состав весового водоизмещения Dс, поэтому сила веса груза не является внешней по отношению к судну. Решение задачи об изменении посадки судна при перемещении на нем груза не ограничивается методом остойчивости; такая задача может быть решена и на основании условия равновесия, т.е. методом плавучести судна (см., например, [3]).
Прием груза на судно
Пусть груз весом Р необходимо принять в точку А с координатами хг, уг, zг. В исходном состоянии судно считается сидящим прямо (θ = 0) и на ровный киль (ψ = 0).
Процесс приема груза удобно рассматривать поэтапно: вначале, условно, груз размещаем на уровне центра тяжести судна, затем перемещаем его на уровень горизонтальной плоскости, в которой он будет оставаться при последующих перемещениях в конечную точку А.
Прием груза на конечный уровень по высоте. На первом этапе груз принимается в точку G0 c координатами 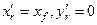 и
и 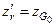 (рис. 2.12), где хf – абсцисса центра тяжести площади начальной ватерлинии.
(рис. 2.12), где хf – абсцисса центра тяжести площади начальной ватерлинии.
Очевидно, что при исходной посадке прямо и на ровный киль, размещение центра тяжести груза в вертикальных плоскостях, проходящих через оси наклонения судна, не вызовет его наклонения.
После приема груза вес судна будет равен 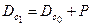 , а средняя осадка
, а средняя осадка 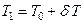 , где
, где
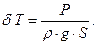 | (2.13) |
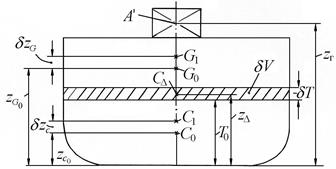 |
Рис. 2.12. Прием груза без наклонения судна
В (2.13) обозначено:
| S | – | площадь действующей ватерлинии, м2; |
| ρ | – | плотность воды, т/м3; |
| g | – | 9,81 м/с2 – ускорение свободного падения. |
На втором этапе центр тяжести груза перемещаем их точки Go в точку  (рис. 2.12). Изменение положения центра тяжести судна
(рис. 2.12). Изменение положения центра тяжести судна  после перемещения груза с уровня
после перемещения груза с уровня  на конечный уровень по высоте, т.е. на уровень
на конечный уровень по высоте, т.е. на уровень 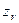 (точка
(точка 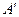 ) можно определить на основании теоремы о перемещении центра тяжести системы:
) можно определить на основании теоремы о перемещении центра тяжести системы:
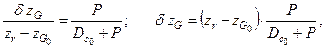 | (2.14) |
| где | 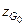 | – | аппликата начального положения центра тяжести судна. |
Прием груза в общем случае вызовет изменение положения центра тяжести судна, центра величины и метацентров.
Если до приема груза поперечная метацентрическая высота составляла 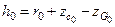 , то после приема ее значение будет определяться как
, то после приема ее значение будет определяться как 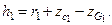
Изменение поперечной метацентрической высоты
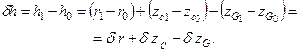 | (2.15) |
Как видно, изменение метацентрической высоты включает три составляющие, которые и нужно вычислить.
Изменение метацентрического радиуса можно найти, исходя из формулы для его определения
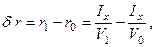
| где | Ix | – | момент инерции площади действующей ватерлинии, который можно считать неизменным в силу того, что при приеме малого груза ватерлиния не изменяется; |
| V1 | – | объемное водоизмещение судна после приема груза; превышает начальное водоизмещения (V0) на величину объема δV, вошедшего в воду (см. рис. 12). |
Преобразуя последнее выражение и перехода от объемов к весам, можно получить
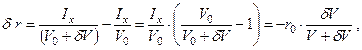
или
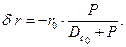 | (2.16) |
Изменение положения центра величины судна, вследствие приема груза и появления по этой причине слоя водоизмещения δV, можно определить аналогично тому, как это показано выше для центра тяжести судна (δzG). Условно будем считать, что в начальный момент центр добавочного слоя водоизмещения совпадает с центром величины судна без груза (точка С0). Затем центр объема перемещаем из точки С0 в точку СΔ с аппликатой 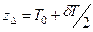 , которая является действительным центром объема δV.
, которая является действительным центром объема δV.
В соответствии с отмеченным по теореме о перемещении центра тяжести системы, можно получить
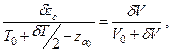
откуда 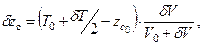
или 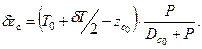 | (2.17) |
Подставив выражения (2.14), (2.16), (2.17) в (2.15), найдем изменение метацентрической высоты
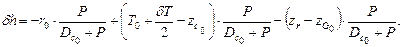
Раскрывая скобки, получим
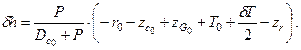
Первые три члена в скобках дают значение начальной метацентрической высоты до приема груза (h0). Учитывая это, можно получить окончательное выражение для изменения поперечной метацентрической высоты
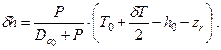 | (2.18) |
В итоге, метацентрическая высота после приема груза определяется по формуле
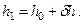 | (2.19) |
Изменение остойчивости удобно оценивать с использованием коэффициентов остойчивости.
Коэффициент поперечной остойчивости судна с грузом можно получить с использованием формул (18) и (19)
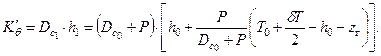 |
После раскрытия скобок и сокращений получаем
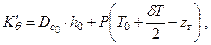
или
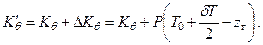 | (2.20) |
Для определения продольной метацентрической высоты и продольного коэффициента остойчивости судна с принятым грузом изложенные выше рассуждения могут быть повторены и получены следующие формулы:
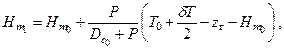 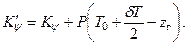 | (2.21) |
Из выражений (2.20) и (2.21) можно выявить условие приема груза без изменения остойчивости судна. Для этого положим равным нулю сомножитель в скобках, т.е. 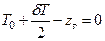 , откуда
, откуда
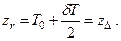
Остойчивость судна не изменяется, если центр тяжести груза (рис. 2.13) располагается на одном уровне с центром тяжести добавочного слоя водоизмещения, т.е. zг = z∆. Этот уровень принято называть «нейтральной плоскостью» при принятии груза.
Если груз принимается ниже центра добавочного слоя водоизмещения, то zг < z∆ и остойчивость судна увеличивается; при zг > z∆ остойчивость уменьшается. В этом нетрудно убедиться, рассмотрев рис. 2.13.
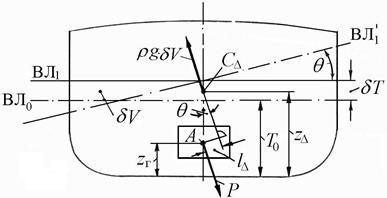 |
Рис. 2.13. К изменению остойчивости при приеме груза
На судно принят груз весом P, у которого цент тяжести располагается в точке А. Вследствие приема груза увеличиваются осадка на δT и объемное водоизмещение – на δV. Сообщим судну (условно) равнообъемное наклонение на угол θ. В этом случае вектора Р и (ρ∙g∙δV) будут направлены перпендикулярно к ватерлинии 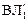 ; они образуют момент, влияющий на остойчивость. Этот момент (∆М = Рl∆) изменяется как по величине, так и по направлению его действия при изменении взаимного положения векторов [Р и (ρ∙g∙δV)] или, иначе, точек
; они образуют момент, влияющий на остойчивость. Этот момент (∆М = Рl∆) изменяется как по величине, так и по направлению его действия при изменении взаимного положения векторов [Р и (ρ∙g∙δV)] или, иначе, точек 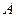 и С∆.
и С∆.
Горизонтальное перемещение груза в конечное положение. Задача об определении посадки судна после приема груза в точку А с координатами хг, уг, zг (конечное положение) решается после нахождения значений веса и средней осадки судна с грузом, а также соответствующих коэффициентов продольной и поперечной остойчивости.
Угол крена судна вычисляется как результат поперечного перемещения груза из точки 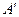 с координатами хf, у = 0, zг в точку
с координатами хf, у = 0, zг в точку 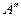 с координатами xf, yг, zг (рис. 2.14). Плечо поперечного перемещения будет равно ординате центра тяжести груза (уг).
с координатами xf, yг, zг (рис. 2.14). Плечо поперечного перемещения будет равно ординате центра тяжести груза (уг).
Угол крена определяется по выражению
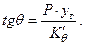
Осадка правого и левого бортов после наклонения с учетом (2.13) определяется по формулам:
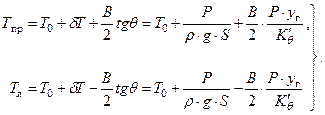 | (2.22) |
При расчете по формулам (2.22) значение ординаты груза (уг) вносится с соответствующим знаком (плюс или минус).
В результате продольного перемещения груза из точки 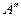 в точку А (рис. 2.14) на расстояние (хг – хf) образуется дифферент судна; тангенс угла дифферента определяется по формуле
в точку А (рис. 2.14) на расстояние (хг – хf) образуется дифферент судна; тангенс угла дифферента определяется по формуле
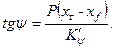 | (2.23) |
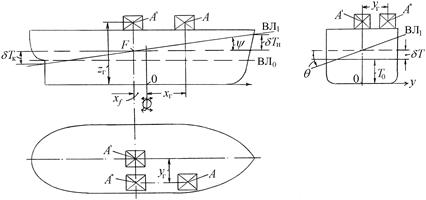 |
Рис. 2.14. К определению посадки при приеме груза
Изменение осадки носом и кормой вследствие появления дифферента:
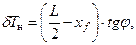 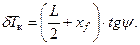 |
Осадки носом и кормой
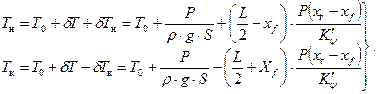 | (2.24) |
При применении формул (2.23), (2.24) значение абсцисс хг и хf вносится с соответствующим знаком (плюс или минус).
2.4.2. Снятие груза с судна (расходование груза)
Путем рассуждений, аналогичных приведенным в п.2.4.1, можно получить зависимости для определения показателей остойчивости и посадки судна после снятия груза. Так, выражения для изменения метацентрических высот (δh, δHm) и новых значений коэффициентов остойчивости ( 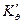 ,
, 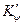 ), принимают вид:
), принимают вид:
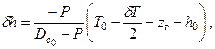 |
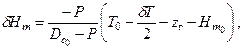 |
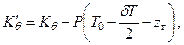 |
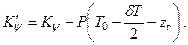 |
Направление изменения остойчивости вследствие снятия груза легко обнаружить наглядным методом (рис. 2.15)
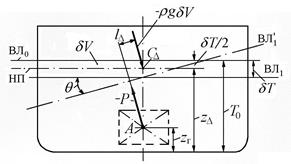 |
Рис. 2.15. К изменению остойчивости при снятии груза
Если центр тяжести снятого груза весом Р находился в точке А, то его удаление равносильно приложению в этой точке вектора силы (-Р).
В результате снятия груза средняя осадка уменьшится на δT, а сила плавучести уменьшится на (ρ∙g∙δV). Потеря силы плавучести равносильна приложению к судну силы (-ρ∙g∙δV) в точке С∆, определяющей положение центра потерянного объема δV (рис. 2.15).
Если судну без груза сообщить (условно) наклонение на угол θ получим ватерлинию  . Векторы [(-Р) и (-ρ∙g∙δV)] при этом будут перпендикулярны ватерлинии
. Векторы [(-Р) и (-ρ∙g∙δV)] при этом будут перпендикулярны ватерлинии  и образуют момент ∆М = Рl∆, который влияет на остойчивость судна.
и образуют момент ∆М = Рl∆, который влияет на остойчивость судна.
Значение ∆М = 0, когда zг = z∆, т.е. когда центр тяжести снимаемого груза совпадает с центром тяжести потерянного объема водоизмещения. Если центр тяжести снятого груза находился ниже «нейтральной плоскости» (НП на рис. 2.15), то остойчивость судна уменьшится, т.к. момент ∆М способствует увеличению наклонения судна (случай по рис. 2.15). При условии zг > z∆ момент ∆М препятствует наклонению – остойчивость судна повышается.
В случае снятия груза для определения характеристик посадки судна могут быть использованы зависимости (2.22) (2.23) (2.24) при условии, что сила Р принимается со знаком минус.
Приведенные выше зависимости для определения осадки носом и кормой при приеме или снятии груза широко используется для решения производственных задач. Они могут быть распространены и на случай, когда на судно действует внешняя сила, вызывающая его дифферент и изменение среднего углубления.
В судоходстве широко распространенным видом приема (удаления) груза является балластировка судна с использованием забортной воды. Ее применяют при изменении массы перевозимого груза и необходимости поддержания определенной посадки с точки зрения погружения винтов, проходимой осадки или прочности корпуса. Кроме того, балластировка и перемещение грузов по длине судна используются для вывода из воды одной из оконечностей корпуса с целью его ремонта.
Решение задачи об изменении продольной посадки судна при приеме (расходовании) груза может быть получено не только методом остойчивости, но и методом плавучести [3].
Начальной остойчивости
Задача о «корабле на камне»
Посадка на мель является одним из наиболее распространенных видов аварий. Возможна и преднамеренная посадка судна на грунт для предотвращения еще большей опасности (ударов о жесткие конструкции или берег, потопления и т.п.).
При посадке на грунт необходимо уметь проводить расчеты, связанные со снятием судна с мели. К ним относятся определение реакции грунта и координат места касания, а также количества и координат центра тяжести груза, который необходимо переместить или снять с судна для его всплытия.
Случай посадки судна на мель без получения пробоины. В первую очередь необходимо определить силу воздействия грунта на корпус судна и координаты точки ее приложения (рис. 2.22). Воздействие грунта можно считать аналогичным снятию груза из точки касания судном дна водоема; тогда из условия равенства потерянной силы плавучести и силы R получим
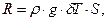
| где | 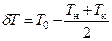 | – | изменение средней осадки; |
| Т0 | – | средняя осадка судна до посадки на мель; | |
| Тн, Tк | – | замеренные осадки судна на мели носом и кормой соответственно. |
 |
Рис. 2.22. К определению воздействия грунта при посадке судна на мель
Значение коэффициента поперечной остойчивости судна после посадки на мель с учетом того, что аппликата условно снятого груза равна нулю ( 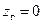 ), можно определить по формуле
), можно определить по формуле
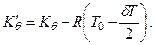
Тогда, при замеренном значении угла крена (θ), ордината точки касания с грунтом находится по выражению
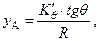 |
или, при известной ширине корпуса (В), а также замеренных осадках правым (Тпр) и левым (Тл) бортами, – по формуле
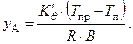
При определении абсциссы точки приложения реакции грунта поправкой к коэффициенту продольной остойчивости можно пренебречь ввиду ее малости по сравнению с начальным значением коэффициента, т.е. считать 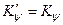 . С учетом этого, абсцисса рассчитывается с использованием зависимости
. С учетом этого, абсцисса рассчитывается с использованием зависимости
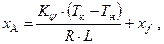
| где | L | – | длина судна. |
После определения силы реакции грунта и координат точки ее приложения к корпусу появляется возможность выполнить расчеты с целью снятия судна с мели. Очевидным способом устранения силы R является приложение к судну, с помощью, например, плавкрана подъемной силы P = R по линии действия силы R.
С этой же целью можно снять или перенести груз с оконечности и борта, сидящих на мели, на противоположные оконечность и борт судна. Решение задачи в этих случаях сводится к определению дифферентующего и кренящего моментов, при действии которых на судно его осадки станут равными замеренным после посадки на мель: Tн, Tк, Tпр, Tл. Для выполнения таких расчетов могут быть использованы зависимости п.2.3 и п.2.4.
При получении пробоины опорная сила реакции грунта увеличивается на вес влившейся воды. Количество влившейся воды определяется методами, используемыми в расчетах по непотопляемости судна.
Вводные замечания
Остойчивость судов при продольных наклонениях, как правило, лежит в пределах применимости метацентрической формулы остойчивости (метода начальной остойчивости). При больших углах дифферента (y > 10°) для определения осадки в оконечностях судна может быть использована диаграмма осадок носом и кормой [3] или диаграмма их изменения [1].
При поперечных наклонениях судов угол крена нередко достигает значений, при которых метацентрическая формула не дает действительной зависимости восстанавливающего момента от угла наклонения.
Остойчивость большинства судов в поперечной плоскости является минимальной. Известные случаи потери остойчивости свидетельствуют, что опрокидывание судов происходит в плоскости близкой к поперечной. Остойчивость судна при больших углах крена является предметом одной из важнейших задач по обеспечению его безопасности – недопущению опрокидывания.
В соответствии с отмеченным, ниже рассматриваются наклонения судна только в поперечной плоскости.
При равнообъемных наклонениях (V= const) в поперечной плоскости ось поворота (продольная ось) судна смещается, по мере увеличения угла крена, в сторону борта наклонения. При большом значении угла крена (q1, рис. 3.1) ось поворота проходит через центр тяжести площади ватерлинии ВЛ1; положение этой оси на рис. 3.1 задано точкой 01. Для сравнения, в методе начальной остойчивости (при малых углах наклонения, см. п. 2.2) положение оси наклонения судна принято (условно) неизменным (по рис. 3.1 – точка 0).
Другим базовым фактором, отличающим метод остойчивости при больших углах крена от метода начальной остойчивости, является учет изменения момента инерции площади равнообъемных ватерлиний от угла крена (для ВЛ0 момент инерции 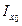 , для ВЛ1 –
, для ВЛ1 – 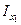 , см. рис. 3.1). По методу начальной остойчивости (см. п.2.1.2) принято:
, см. рис. 3.1). По методу начальной остойчивости (см. п.2.1.2) принято: 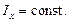
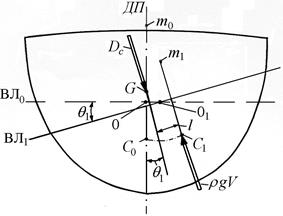 |
Рис. 3.1. плечо статической остойчивости при больших наклонениях
Изменение момента инерции площади ватерлинии вызовет изменение величины метацентрического радиуса (на рис. 3.1: 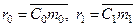 ) и положения метацентра (точки m0, m1). Соответственно изменяется и радиус кривизны траектории центра величины (траектории перемещения точки С). Траектория будет отличаться от окружности, положенной в основу при выводе метацентрической формулы остойчивости.
) и положения метацентра (точки m0, m1). Соответственно изменяется и радиус кривизны траектории центра величины (траектории перемещения точки С). Траектория будет отличаться от окружности, положенной в основу при выводе метацентрической формулы остойчивости.
Отмеченные обстоятельства существенно меняют зависимость восстанавливающего момента от угла крена.
Метацентрический радиус при поперечном наклонении определяется по формуле
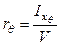 , , |
| где | 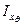 | – | центральный поперечный момент инерции площади равнообъемной ватерлинии при угле крена q; |
| V = const | – | неизменное при наклонении объемное водоизмещение. |
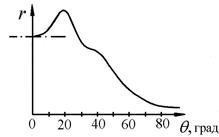 Рис. 3.2. зависимость поперечного метацентрического радиуса от угла крена Рис. 3.2. зависимость поперечного метацентрического радиуса от угла крена | Характерный вид кривой 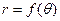 представлении на рис. 3.2. Горизонтальная касательная при θ = 0 (рис. 3.2) незначительно отстоит от кривой при малых наклонениях (θ ≤ 10°), так как при этом слабо меняется момент инерции площади ватерлинии. представлении на рис. 3.2. Горизонтальная касательная при θ = 0 (рис. 3.2) незначительно отстоит от кривой при малых наклонениях (θ ≤ 10°), так как при этом слабо меняется момент инерции площади ватерлинии. |
Зависимость r = f(θ) полностью определяет траекторию перемещения центра величины. Она может быть рассчитана в координатах «y–z» с использованием зависимостей
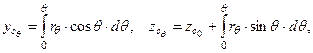 | ||||
| где | 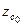 | – | аппликата центра величины при q = 0. |
При известных значениях 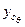 и
и 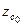 координаты соответствующего метацентра определяются по формулам
координаты соответствующего метацентра определяются по формулам
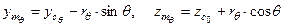 . . |
Траектории перемещения центра величины (C) и метацентра (т) принято представлять на «полярной диаграмме поперечной остойчивости», которая представляет собой специальное геометрическое построение. Полярная диаграмма служит для комплексного представления зависимостей пяти параметров остойчивости от угла крена (подробнее см. [4]);зависимости по трем основным параметрам даны на рис. 3.3.
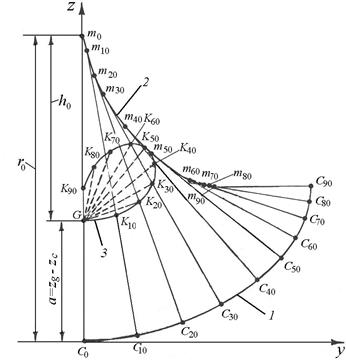 |
Рис. 3.3. Кривая центров в
