Автоматизированные системы обработки информации

Автоматизированные системы обработки информации

Брест 2013

УДК 347 77/.

ББК 67.403.3 73/.

В методических указаниях приведены краткие теоритические сведения, необходимые для выполнения лабораторных работ, рассмотрены практические примеры использования методов. Методические указания содержат описание шести лабораторных работ с вариантами индивидуальных заданий к ним.

Методические указания предназначены для использования студентами специальности 1-53 01 02Автоматизированные системы обработки информации в ходе выполнения лабораторных работ по дисциплине «Вычислительная математика».

Составитель	Глущенко Т.А.	старший преподаватель кафедры ИИТ
Рецензент	Матюшков Л.П.	доцент кафедры экономики и управления Учреждения образования «Брестский государственный университет» им. А.С.Пушкина, к.т.н., доцент

Учреждение образования

© «Брестский государственный технический университет», 2013

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 4

ЛАБОРАТОРНАЯ РАБОТА №1. Решение нелинейных уравнений. 5

ЛАБОРАТОРНАЯ РАБОТА №2. Итерационные методы решения СЛАУ. 14

ЛАБОРАТОРНАЯ РАБОТА №3. Интерполирование функций. 24

ЛАБОРАТОРНАЯ РАБОТА №4. Численное интегрирование. 30

ЛАБОРАТОРНАЯ РАБОТА №5. Численное решение задачи Коши для дифференциальных уравнений 1 – го порядка. 41

ЛАБОРАТОРНАЯ РАБОТА №6. Решение задачи Коши для системы дифференциальных уравнений 1-го порядка. 49

ЛИТЕРАТУРА 56

ВВЕДЕНИЕ

Вычислительная математика является важной составляющей в системе подготовки инженеров специальности «Автоматизированные системы обработки информации», т.к. рассматривает методы обработки математической информации. И при этом вычислительная математика является динамической дисциплиной, поскольку с ростом быстродействия ЭВМ и появления новых компьютерно-информационных технологий, разрабатываются все новые и боле сложные вычислительные алгоритмы решения математических задач.

Данное методическое пособие разработано в соответствии с учебной программой по дисциплине «Вычислительная математика» для специальности 1-53 01 02 Автоматизированные системы обработки информации. Пособие содержит описание шести лабораторных работ по следующим разделам: решение нелинейных уравнений, решение систем линейных алгебраических уравнений, интерполирование, численное интегрирование, решение задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка и решение задачи Коши для систем обыкновенных дифференциальных уравнений 1-го порядка.

В каждой лабораторной работе содержатся варианты заданий. С учетом специфики специальности АСОИ все рассматриваемые методы предполагают программную реализацию. При этом каждый метод в конкретной работе должен быть реализован в виде отдельной функции и, если указано точное решение, должен быть предусмотрен вывод значений как точного, так и приближенного решений различными методами. Выполнение лабораторной работы предполагает также анализ полученных результатов: при необходимости оценка абсолютной погрешности метода, сравнение количества итераций в методах, анализ скорости сходимости.

По результатам выполнения каждой работы должен быть представлен отчет.

ЛАБОРАТОРНАЯ РАБОТА №1. Решение нелинейных уравнений.

Задание.

1. Построить график функции f(x).Отделить все корни, лежащие на данном отрезке.

2. Вычислить наибольший из корней уравнения методом в соответствии с вариантом. Варианты заданий указаны в таблице 1.1. Точность нахождения корня . При необходимости предусмотреть проверку выполнения достаточных условий сходимости метода. Выбрать два различных начальных приближения из отрезка изоляции корня, провести вычисления, сравнить число итераций.

3. Вычислить невязку решения уравнения 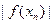, где 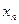- приближенное значение корня.

4. Геометрически проиллюстрировать сходимость метода для своего уравнения.

Таблица 1.1 - Варианты заданий.

№ вар.	f(x)	Отрезок	Метод
a	b
1.		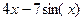-2		хорд
2.		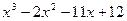-4		Ньютона
3.		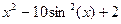-1		Вегстейна
4.		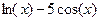		хорд
5.		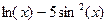		Вегстейна
6.		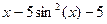		бисекции
7.		-12		хорд
8.		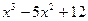-2		Ньютона
9.		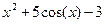-4		Вегстейна
10.		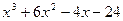-8		хорд
11.		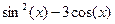-7		Ньютона
12.		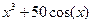-4		бисекции
13.		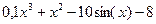-4		Вегстейна
14.		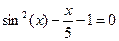-4		Ньютона

Метод простой итерации.

Рассмотрим СЛАУ в виде (2.2):

.

Преобразуем систему к виду:

(2.3)

Приведение системы вида (2.2) к виду (2.3) можно осуществить различными способами. Например, можно выполнить эквивалентные преобразования:

,

где α - некоторый параметр, подбирая который можно влиять на сходимость метода, E– единичная матрица.

Или, если матрица А имеет ненулевые диагональные элементы, то i-е уравнение делят на элемент , чтобы получить единичный коэффициент перед x_i. Затем в i-м уравнении в левой части оставляют x_i, а все остальные слагаемые переносят в правую часть. Получаем систему вида , где:

(2.4).

В развернутой форме система имеет вид:

(2.5)

Пусть теперь система записана в виде (2.3). Зададим произвольным образом начальное приближение и подставим его в правую часть системы (2.3). Получим 1-е приближение.

.

Вновь подставим полученное приближение в правую часть системы (2.3), получим 2-е приближение и т.д. Повторяя процесс подстановок k раз, на k- итерации мы получаем k-е приближение:

. (2.6)

Здесь

Организуя, таким образом, итерационный процесс, получаем рекуррентную последовательность приближений : . Вычисление последовательности приближений по формуле (2.6) называется методом простых итераций. Итерационный процесс должен быть построен таким образом, чтобы последовательность приближений с ростом k стремилась к решению системы (2.3).

Достаточное условие сходимости метода простых итераций дает следующая теорема.

Теорема. Пусть . Тогда система (2.3) имеет решение, причем единственное, и последовательность приближений сходится к этому решению со скоростью геометрической прогрессии (при любом начальном приближении ).

Выполнение условия берется по любой матричной норме: кубической евклидовой, октаэдрической.

Из теоремы следует, что метод простых итераций сходится, если выполняется хотя бы одно из условий:

1. , (по кубической норме матрицы)

2. , (по евклидовой норме) (2.7)

3. . (по октаэдрической норме)

Если условие (2.7) выполняется, начальное приближение может быть выбрано любым. Например, можно положить .

В частном случае представления системы вида (2.3) в виде (2.5), развернутая форма для итераций принимает вид:

Погрешность k-го приближения в методе простых итераций оценивается неравенством:

(2.8)

Заметим, что чем меньше норма матрицы ||B||, тем быстрее сходятся итерации.

При решении СЛАУ обычно используют кубическую норму вектора и матрицы.

Из оценки (2.8) следуют и условия остановки итерационного процесса. Пусть требуется найти решение системы (2.2) с точностью . Тогда, если норма матрицы , итерации продолжаются до тех пор, пока не выполнится условие:

(2.9)

Введем обозначение: q=||B||. Тогда, если норма матрицы ||B||>1/2, итерации заканчиваются, когда выполнится условие:

(2.10)

а

где - допустимая абсолютная погрешность нахождения решения СЛАУ. Эти условия должны быть выполнены по (k)и (k-1)приближениям для всех неизвестных. Например, первое условие (2.9) можно представить через логическое «и» в виде:

.

Метод Зейделя.

Метод Зейделя является модификацией метода простых итераций. Как и в методе простых итераций приведем систему вида (2.2) каким-либо способом к виду (2.3).

При применении метода простых итераций, в общем случае итерации осуществлялись бы по формуле:

, (2.11)

При этом значения (k) приближения по всем неизвестным можно было бы вычислять в любом порядке. Идея метода Зейделя состоит в том, чтобы использовать уже найденные приближения для улучшения значения последующих приближений , т.е. проводить вычисления по формуле:

, (2.12)

Метод вычисления решения на основе итерационной последовательности (2.12) называется методом Зейделя.

Такое усовершенствование позволяет ускорить сходимость метода Зейделя по сравнению с методом простых итераций почти в два раза.

Запишем развернутую форму для итераций метода Зейделя для системы вида (2.5):

(2.13)

Формулу для итераций системы вида (2.5) метода Зейделя можно записать в другом виде. Разложим матрицу B вида (2.4) в сумму двух строго треугольных (нулевые элементы главной диагонали) матриц, т.е. положим , где:

В этом случае система (2.3) приобретет вид:

.

А метод Зейделя соответственно запишется в виде:

(2.14)

Достаточным условием сходимости метода Зейделя является условие доминирования диагональных элементов в матрице A построкам или по столбцам:

, или , . (2.15)

Сформулированные условия преобладания диагональных элементов являются достаточными, поэтому возможны случаи невыполнения этих условий при сходимости метода.

В частном случае системы вида (2.5) достаточные условия сходимости (2.7) метода простых итераций приобретают вид (2.15). Таким образом, для нашего частного случая достаточными условиями сходимости для обоих методов являются условия доминирования диагональных элементов в матрице A построкам или по столбцам.

Часто для обеспечения сходимости методов бывает достаточно поменять местами уравнения системы с тем, чтобы на главную диагональ матрицы A системы встали максимальные по абсолютной величине коэффициенты.

Для системы вида (2.5) в методе Зейделя в случае выполнения условия справедлива следующая апостериорная оценка абсолютной погрешности k-приближения:

(2.16)

Из оценки (2.16) следуют и условие остановки итерационного процесса. Введем обозначение: ..Итерации продолжаются до тех пор, пока не выполнится условие:

(2.17)

Для контроля полезно найти невязку полученного решения :

(2.18)

Рассмотрим итерационные методы на примере.

Пусть требуется решить СЛАУ с точностью .

(2.19)

Точное решение системы: . Система из 3-х уравнений, с 3 неизвестными, определитель матрицы, , система имеет единственное решение. Сразу заметим, что в системе выполняется достаточное условие сходимости (доминирование диагональных элементов матрицы A) и оба метода будут сходиться к решению системы. Диагональные элементы матрицы , поэтому в соответствии с рекомендациями, из первого уравнения выразим , из второго , из третьего .

Получим:

(2.20)

Соответственно, матрица B и вектор-столбец свободных членов имеют вид:

Вычислим нормы матрицы B.

Кубическая норма матрицы определяется как максимальное значение из сумм элементов каждой строки, взятых по модулю.

.

Евклидова норма матрицы вычисляется через корень квадратный из суммы квадратов всех элементов матрицы B.

.

Октаэдрическая норма матрицы определяется как максимальное значение из сумм элементов каждого столбца, взятых по модулю.

.

Решим СЛАУ методом простой итерации.

Зададим произвольное начальное приближение: .

Подставим начальное приближение в правую часть системы (2.20), и на 1-ой итерации получим 1-ое приближение: .

Подставив 1-е приближение в правую часть системы (2.20), получим 2- приближение. На 2-ой итерации имеем:

Проверим выполнение условия прекращения итераций. Т.к. норма матрицы , применять будем условие (2.10). Оно принимает вид:

,

поэтому итерации продолжаются.

Продолжая процесс подстановок, на 11 итерации получим решение системы с заданной точностью: . Как мы уже говорили, при выполнении условия сходимости (2.7), начальное приближение может быть выбрано любым. Возьмем, например, начальное приближение : . На 10 итерации получим решение системы с заданной точностью.

Метод Зейделя.

1-я итерация:

Подставим то же начальное приближение в первое уравнение системы (2.16), получим . При вычислении значения используем только что полученное значение . Имеем: . При вычислении , подставим в 3-е уравнение полученные на 1-ой итерации значения . Получим: .

2-я итерация:

После двух итераций проверим выполнение условия (2.15). Матрица в нашем случае имеет вид:

Ее кубическая норма равна . Условие (2.8) приобретает вид:

.

Как видим, погрешность нахождения решения на второй итерации в методе Зейделя меньше, чем в методе простых итераций. На 6 итерации, получим решение системы: .

Вычислим по формуле (2.14) невязку полученного решения. Для этого для каждого уравнения системы (2.15) вычислим абсолютную величину разности между значениями правой части уравнения и значением левой части уравнения при подстановке в него полученных значений неизвестных. Максимальная из полученных величин и даст нам невязку приближенного решения. Например, для первого уравнения имеем:

.

Произведя вычисления по всем уравнениям, имеем:

.

Задание.

1. Решить СЛАУ методом простых итераций и Зейделя согласно варианту. Варианты заданий указаны в таблице 2.1. Предусмотреть проверку достаточных условий сходимости методов. Точность нахождения решения СЛАУ .

2. Вычислить невязку полученного решения.

Таблица 2.1 - Варианты заданий

№	Матрица системы A	Вектор- столбец свободных членов
1.
2.
3.
4.
5.
6.
8.
9.
Продолжение таблицы 2.1 - Варианты заданий
10.
11.
12.
13.
14.

Задание.

1. Построить полином Лагранжа и Ньютона на равномерной сетке узлов для указанной функции на заданном отрезке 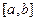согласно варианту. Варианты заданий указаны в таблице 3.1. Вычислить значение функции и полинома в точке .

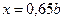2. Вычислить реальную абсолютную погрешность интерполирования в точке .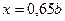

Таблица 3.1 - Варианты заданий

№	Функция	Отрезок	Число узлов
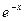		[0,4]
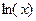		[1,4]
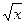		[0,4]
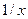		[1,4]
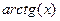		[0,2]
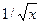		[1,4]
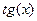		[0,1.5]
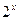		[0,4]
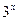		[0,2]
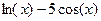		[1,6]
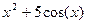		[1,6]
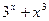		[-1,2]
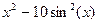		[0,3]
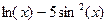		[3,6]

Задание.

1. Вычислить точное значение определенного интеграла, указанного в варианте. Варианты заданий указаны в таблице 4.4.

2. Вычислить приближенное значение определенного интеграла с шагом 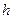и 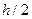методом согласно варианту. Количество частичных отрезков 6 и 12 соответственно. Оценить погрешность вычисления с шагом 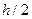по правилу Рунге.

3. Методом неопределенных коэффициентов построить интерполяционную квадратурную формулу на 4 равностоящих узлах, вычислить интеграл.

4. Вычислить определенный интеграл по формуле Гаусса-Кристоффеля на 2 и 3 узлах соответственно.

5. Сравнить методы по точности; оценить фактическую погрешность вычисления интеграла по составной формуле с шагом 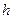и 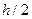. Полученные результаты свести в итоговую таблицу.

Таблица 4.4 – Варианты заданий

№	Определенный интеграл	Методы
1.		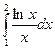средних прямоугольников
2.		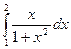трапеций
3.		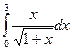Симпсона
4.		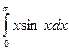средних прямоугольников
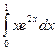		трапеций
6.		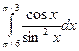средних прямоугольников
7.		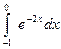Симпсона
8.		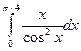трапеций
9.		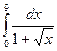Симпсона
10.		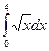трапеций
11.		средних прямоугольников,
12.		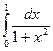Симпсона
13.		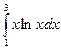трапеций
14.		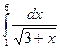Симпсона

Задание.

1. Решить задачу Коши для ОДУ 1–го порядка методом Рунге–Кутта 4-го порядка. Количество узлов – 6. Сгустить сетку, вычислить значения решения с шагом 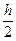. Произвести оценку погрешности приближенного решения 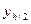по правилу Рунге

2. Решить ОДУ методом в соответствии с вариантом.

3. Сравнить значения точного и приближенного решений различными методами на сетке с шагом 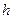, сделать выводы.

Таблица 5.3 - Варианты заданий

№	ОДУ	Начальные условия	Отрезок	Точное решение уравнения	Метод
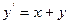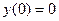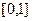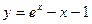					Эйлера
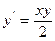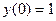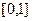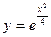					Эйлера-Коши
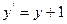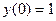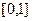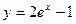					Эйлера
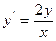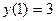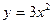					мод. метод Эйлера
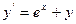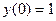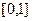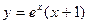					Эйлера-Коши
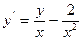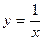					мод. метод Эйлера
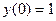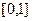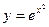					Эйлера-Коши
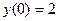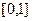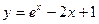					Эйлера
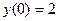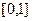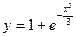					мод. метод Эйлера
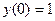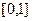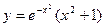					Эйлера-Коши
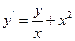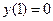					мод. метод Эйлера
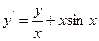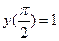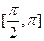					Эйлера
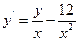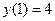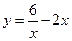					Эйлера-Коши
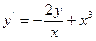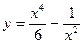					мод. метод Эйлера

Задание.

1. Решить СДУ согласно варианту методом Рунге-Кутты четвертого порядка, ДУ 2-го порядка, предварительно приведя его к СДУ, решить методом Рунге-Кутты второго порядка. Количество узлов – 8.

2. Сравнить значения точного и приближенного решений, сделать выводы.

Таблица 6.2 - Варианты заданий

№	ДУ или СДУ	Начальные условия	Отрезок [a,b]	Точное решение ДУ или СДУ
1.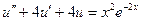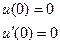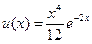
2.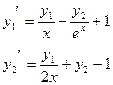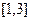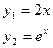
3.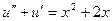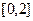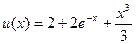
4.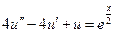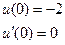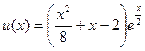
5.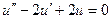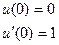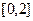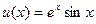
6.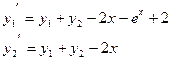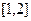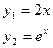
7.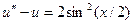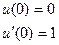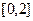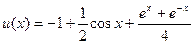
8.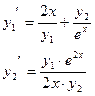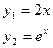
9.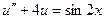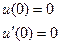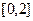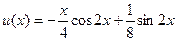
10.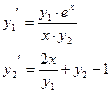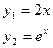
11.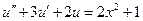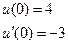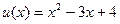
12.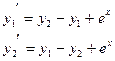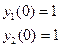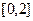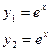
13.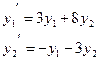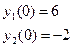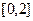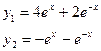
14.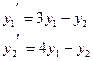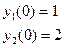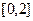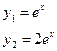

ЛИТЕРАТУРА

1. Бахвалов Н.С. Численные методы. – М.:БИНОМ, 2004.

2. Калиткин Н.Н. Численные методы. – М.: Наука, 1978.

3. Волков Е.А. Численные методы. - М: Наука, 1982.

4. Самарский А.А., Гулин А.В. Численные методы. — М: Наука, 1989.

5. Мудров, А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП РАСКО, 1991.

6. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженера – М.: Высшая школа,1994.

7. Вержбицкий В.М. Численные методы – М.: Высшая школа, 2005,
866 с.

8. Рябенький В.С. Введение в вычислительную математику: Учебное пособие. – 2-е изд., исправл. – М.:ФИЗМАТЛИТ, 2000, 296 с.

9. Петров И.Б., Лобанов А.И. Лекции по вычислительной математике: Учебное пособие – М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория знаний, 2006, 523 с.

10. Бабенко К.И. Основы численного анализа. – Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2002, 848 с.

11. Сю.

12. Ол.

УЧЕБНОЕ ИЗДАНИЕ

Составитель: Глущенко Татьяна Александровна

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ

по дисциплине «Вычислительная математика»

для студентов специальности

1-53 01 02 Автоматизированные системы обработки информации

Ответственный за выпуск: Глущенко Т.А.

Редактор: Боровикова Е.А.

Компьютерная верстка:

Корректор:

Подписано к печати _____________ Формат 60х84 1/16.Бумага писч.

Усл. печ. лист. ______ Уч.изд.л. _______ Тираж 30 экз. Заказ № _________

Отпечатано на ризографе учреждения образования

«Брестский государственный технический университет».

224017, г. Брест, ул. Московская, 267

Автоматизированные системы обработки информации

Брест 2013