Методы оценки временных рядов

1. Параметрические — рассматривают временной ряд как гладкую функцию от t: 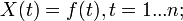. При этом сначала выявляют один либо несколько допустимых типов функций 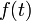; затем различными методами (например, МНК) оценивают параметры этих функций, после чего на основе проверки критериев адекватности выбирают окончательную модель тренда. Важное значение для практических приложений имеют линеаризованные тренды, то есть тренды, приводимые к линейному виду относительно параметров использованием тех или иных алгебраических преобразований.

2. Непараметрические — это разные методы сглаживания исходного временного ряда — скользящие средние (простая, взвешенная), экспоненциальное сглаживание. Эти методы применяются как для оценки тренда, так и для прогнозирования. Они полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.

Основная тенденция временного ряда не всегда может быть определена визуально, поэтому применяют специальные критерии проверки гипотезы о наличии тренда в ряду динамики, после чего уже строится модель тенденции как функции времени.

3.1. Методы определения наличия тенденции

Для диагностирования наличия тенденции наиболее широко применяются метод сравнения средних и метод Фостера-Стюарта.

А) Метод сравнения средних. Метод сравнения средних применим для выявления монотонной тенденции.

Временной ряд разбивается на две примерно равные части у₁,у₂, ..., у_n1 и у_n1+1, у_n1+2, …, у_n=n1+n2 с количеством уровней n₁ и n₂ и для каждой части вычисляются средние ( 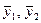) и выборочные дисперсии (s²₁, s²₂) соответственно.

Далее если предполагается, что значения дисперсии на этих участках не равны между собой, т. е. 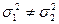, то значение критерия Стьюдента рассчитывается по формуле

,

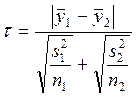а если предполагается, что дисперсии одинаковы 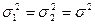, то значение критерия Стьюдента рассчитывается по формуле 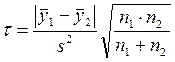, где s² - общая выборочная дисперсия ряда.

Нулевая гипотеза о равенстве средних (об отсутствии тенденции) отвергается, если выполняется услови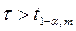е , где 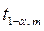- табличное значение t-критерия Стьюдента при уровне значимости α и числе степеней свободы m = n₁ + n₂ - 2.

Б) Метод Фостеpa-Стюарта. Является более универсальным и дает более надежные результаты.

На первом этапе каждый уровень временного ряда y_t (t = 1..n) сравнивается со всеми предыдущими уровнями. На основании результатов сравнений определяются вспомогательные величины q_t и p_t:

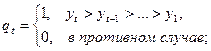
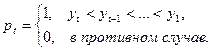
После этого находится ряд значений d_t = q_t – p_t.

На втором этапе все значения d_t суммируются, и определяется величина D:

.

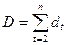Основная гипотеза об отсутствии тренда в изучаемом временном ряде проверяется с помощью t-критерия Стьюдента. При этом сравниваются наблюдаемое и табличное значения t-критерия Стьюдента. Наблюдаемое значение t-критерия определяется по формуле:

,

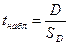где S_D — стандартное отклонение величины D. Значения S_D для временных рядов, длиной от 10 до 100 наблюдений, представлены в специальной таблице.

Критическое значение t-критерия t_крит (α, n − 1) определяется по таблице распределения Стьюдента в зависимости от уровня значимости α и числа степеней свободы n - 1.

Если |t_набл| ≥ t_крит, то основная гипотеза об отсутствии тенденции в исследуемом временном ряде отвергается.

Если |t_набл| < t_крит, то в изучаемом временном ряде тренд отсутствует.