Глава 7. Методы обработки экспериментальных данных

Построение эмпирической формулы.

Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости y(x).

x	x1	x2	…	xn
f(x)	y1	y2	…	yn

Требуется подобрать формулу, которая выражает данную зависимость аналитически. Такая формула называется эмпирической.

Мы уже рассматривали один из подходов к решению данной задачи, он состоит в построении интерполяционного многочлена, значения которого будут совпадать в точках x_i с соответствующими табличными значениями f(x_i), где i=1,2..n. Но совпадения значений в узлах может вовсе не означать совпадение характеров исходной и интерполирующей функции. Требование совпадения значений тем более не оправдано, если значение функции f(x) известны с некоторой погрешностью. Поставим задачу так, чтобы с самого начала находить функцию заданного вида , которая в точках x_1, x_2… x_n принимает значения как можно более близкие к табличным значениям y_1, y_2… y_n . Так как точную функциональную зависимость подобрать достаточно сложно, выбирают простые по виду аналитические функции, а затем устанавливают параметры этой функции. Самая простая линейная зависимость , у неё два параметра а и b . Подберем их различными методами.

Метод выбранных точек (метод натянутой нити)

Рис 7.1.Метод выбранных точек

Выбираются точки наиболее удаленные друг от друга x₁ x_n, затем составляются уравнения прямых, проходящих через эти точки. Из полученной таким образом системы находятся неизвестные параметры прямой а и b

, , .

Метод средних

Отклонением точки (x_i,y_i )от кривой назовем ε_i -разность между значением кривой в точке x_i и табличным значением y_i Лучшим положением кривой , считается такое, при котором отклонение точек от нее минимально. Количество точек делится на две части так, чтобы в каждой части, суммы ординат этих точек примерно совпадали. По каждой группе точек составляется сумма отклонений и приравнивается к нулю. Из системы находим a и b

, ,

.

Метод натянутой нити и метод средних не очень точны и используются обычно на предварительном этапе обработки данных для того чтобы прикинуть результаты. Рассмотрим более точный метод аппроксимации для линейной функции

Метод наименьших квадратов

Задача наименьших квадратов возникает в самых различных областях науки и техники, например, при статистической обработке данных.

Для линейной зависимости y=ax+b составляем функцию, которая представляет собой сумму квадратов отклонений от прямой: , где ( 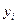-табличное значение, - эмпирическая формула). Надо определить такие значения параметров a и b , при которых функция двух переменных достигает минимума. Необходимым условием для этого является равенство нулю частных производных по a и b.

Возьмем частные производные по переменным a и b, приравняем их к нулю:

Получим систему линейных уравнений относительно неизвестных

a и b. Система называется нормальной для метода наименьших квадратов. Решаем систему по правилу Крамера:

Если обозначить: , ,

, , то тогда можно записать

и .

Метод выравнивания

К линейной функции можно привести любую функцию вида ψ(y)=aּφ(x)+b, для этого достаточно сделать замену переменных, z=ψ(y), t=φ(x). Тогда мы получим z=aּt+b.

Рассмотрим показательную функцию .

Прологарифмируем это равенство. Получим ln(y)=ln(a)+x ln(b). Сделаем замену переменных z= ln(y), t=x и обозначим А= ln(b) B= ln(a). После замены получим z=A t+b.

Аналогично делаются замены и для других функций из таблицы.

Таблица 7.1.

Таблица замен

№	Вид функции	Замена переменных	Характерные точки	Отклонения
1.
2.
3.
4.
5.
6.
7.

, , .

, , .

- табличное значение для x_ар;

- табличное значение для х_геом;

- табличное значение для х_гарм.

В таблице может не оказаться точек тогда точки , доопределяют по соседним точкам таблицы с помощью линейной интерполяции.

Для аналитических кривых существуют характерные точки, которые лежат на этих кривых. Например, если две точки принадлежат прямой, то и точка с координатами ( , ) принадлежит той же прямой, если две точки принадлежат гиперболе, то и точка (x_ар,y_гарм) также принадлежат этой гиперболе. В таблице через обозначено отклонение табличного значения , соответствующего x_ар, от ординаты характерной точки , через - отклонение табличного от ординаты характерной точки y_гарм и т.д.

Остальные находятся аналогично, в зависимости от характерных точек. Функция, для которой примет наименьшее значение и будет наиболее подходящей. После соответствующей замены переменных применяют метод наименьших квадратов.

Пример 7.1

Бомба «Рейда» это техническое устройство для изучения легкоиспаряющихся жидкостей. В эксперименте на бомбе «Рейда» при постоянной температуре измеряется манометром избыточное давление паров нефти при различных соотношениях объёмов газовой и жидкой фаз. Определить эмпирическую зависимость давления паров нефти от соотношения объёмов газовой и жидкой фаз методом наименьших квадратов. Набор экспериментальных данных представлен в таблицах

Для того, чтобы выбрать наиболее подходящую зависимость построим график по табличным данным

Можно предположить, что это будет :

1. показательная функция (строка 2 таблицы 7.1),

2. степенная функция (строка 5 таблицы 7.1),

3. дробно–рациональная функция (строка 3 таблицы 7.1).

Выберем ту функцию, для которой примет наименьшее значение.

В таблице данных нет значений , , , подставляя , , вместо v в формулу для линейной интерполяции, найдем соответствующие им значения функции , , .

Формула для вычисления табличного значения для , , , с помощью линейной интерполяции

Самые маленькие . Найдем методом выравнивания параметры для выбранных видов зависимостей. Будем искать аппроксимирующую функцию в виде

.

Делаем замену переменных

После замены точки ложатся близко к прямой. Параметры этой прямой A и B

После замены z = At + B нашли A и B по методу наименьших квадратов, используя встроенные функции Mathcadа.

Функция slope(x,y) возвращает значение углового коэффициента.

Функция intercept(x,y) возвращает значение свободного параметра.

Возвращаемся к исходной функции , строим её график и находим сумму квадратов отклонений от исходной таблицы значений. Можно также найти и среднеквадратичное отклонение.

.

Из двух разных приближений одной и той же табличной функции лучшим считается то, для которого сумма квадратов отклонений меньше.

Для этой же таблицы данных рассмотрим приближение, заданное показательной функцией

.

Замена переменных

среднеквадратичное отклонение.

сумма квадратов отклонений

Для этой же таблицы данных рассмотрим приближение, заданное дробно-линейной функцией .

Рис. 7.2. Решение примера 7.1 в Mathcad

Лучшим приближением для этих экспериментальных данных будет степенная функция.