Глава 6. аппроксимация функций с помощью сплайнов

При большом количестве узлов интерполяции приходится использовать интерполяционные полиномы высокой степени, что создает определенные неудобства при вычислениях. Можно избежать высокой степени интерполяционного многочлена, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Однако такое интерполирование обладает существенным недостатком: в точках сшивки разных интерполяционных полиномов будет разрывной их первая производная, поэтому для решения задачи кусочно-линейной интерполяции используют особый вид кусочно-полиномиальной интерполяции — сплайн-интерполяцию. Сплайн — это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.

Математически сплайны моделируют старое механическое устройство из гибких реек. Если их жестко закрепить в узлах интерполяции, то рейки принимают форму, минимизирующую их потенциальную энергию

Основные характеристики сплайнов:

- количество и расположение узлов;

- наибольший порядок m многочлена, из которого склеен сплайн;

- гладкость сплайна в узлах.

Пусть на отрезке 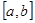задана функция аналитически (в виде 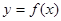), таблично или графически. Для замены этой функции сплайном разобьем отрезок 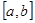на n частей и составим таблицу:

Функция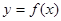

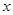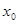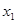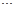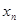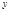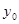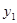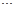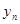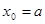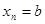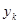Здесь , , а - значения функци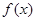и при .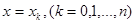

Дадим математическое определение сплайна. Сплайном степени m называется функция 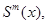удовлетворяющая следующим свойствам:

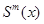непрерывна на 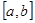вместе со всеми производными до некоторого порядка р;

На каждом отрезке 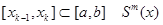совпадает с некоторым многочленом P_m,k(x) степени m

Пусть в каждой точке 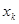существует непрерывная производная 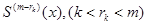. А следующая производная 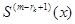может быть уже разрывная. Дефектом в сплайне называется число 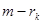в точке 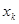. Если мы возьмем 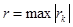, то это тоже дефект сплайна.

Интерполяция ломаными это самый простой сплайн первой степени с дефектом, равным единице. В этом случае сама функция непрерывна, а уже первая производная разрывная. Если функция задана таблично, то значения 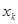выбираем из таблицы; при этом, чем больше n, тем лучше аппроксимация. На каждом из элементарных отрезков 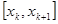заменяем функцию 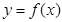отрезком прямой: .

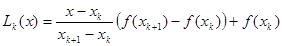Кубические сплайны

При рассмотрении изгиба изогнутость приходится представлять кривой более высоких порядков. В этом случае часто применяют кубические сплайн функции, когда функция 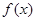интерполируется на каждом элементарном отрезке кубическим многочленом. На отрезке 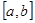оси Ox зададим равномерную сетку с шагом 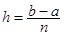, в узлах 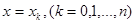зададим значения 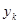функции 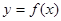, определенной на отрезке .

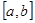Внутри каждого элементарного отрезка 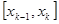заменим функцию 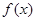функцией 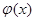, удовлетворяющей следующим условиям:

1. 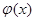непрерывна на 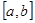вместе со своими производными первого и второго порядка;

2. 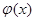на каждом отрезке 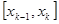является кубическим многочленом:

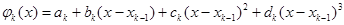(6.1) ;.

3. в узлах сетки 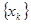выполняется равенство ;

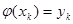4. 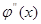удовлетворяет граничным условиям .

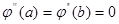Требуется найти четверку неизвестных коэффициентов 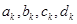для всех 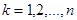Можно доказать, что задача нахождения кубического сплайна имеет единственное решение.

Потребуем выполнения третьего условия, совпадения значений функции 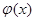в узлах с табличными значениями;

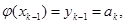(6.2)

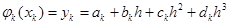(6.3)

Число полученных уравнений 2n в два раза меньше числа неизвестных коэффициентов. Для составления оставшихся уравнений воспользуемся первым условием о непрерывности производных сплайна во всех точках. Приравняем левые и правые производные во внутреннем узле x_k 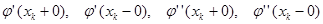, вычислив предварительно выражение для производных 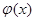последовательным дифференцированием (6.1)

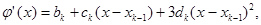(6.4)

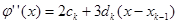(6.5)

Найдем правые и левые производные в узле:

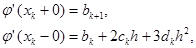
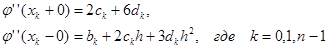
Приравняв левые и правые производные, получим для:

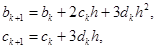
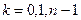(6.6)

Уравнения (6.6) дают еще 2(n-1) условий. Для получения недостающих уравнений накладывают требования к поведению сплайна на концах отрезка 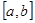. При нулевой кривизне, когда вторая производная равна нулю, например, получим:

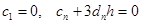(6.7)

Исключив из уравнений (6.2)- (6.6) неизвестные a_k, получим систему из 3n уравнений:

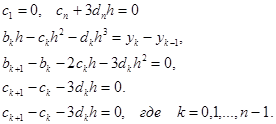(6.8)

Решив эту систему, мы найдем значения неизвестных a_k,b_k,c_k определяющих совокупность формул для искомого интерполяционного сплайна

Для вычисления коэффициентов сплайнов в Mathcad предназначены функции, возвращающие массив коэффициентов:

cspline(x,y)-кубического сплайна;

pspline(x,y)-квадратичного сплайна;

lcspline(x,y)-линейного сплайна;

Во всех этих функциях х-массив абсцисс , а y- массив ординат экспериментальных точек. После вычисления коэффициентов сплайнов можно вычислить значение интерполяционного полинома в конкретной точке t, обратившись к функции interp(x,U,P,t), где х- массив коэффициентов сплайнов

Пример 6.1 В результате опыта холостого хода определена таблица зависимости потребляемой из сети мощности P от выходного напряжения U для асинхронного двигателя. Построить график интерполяционной зависимости. При решении воспользуемся встроенными функциями сплайновой аппроксимации в Mathcad

Экспериментальные точки

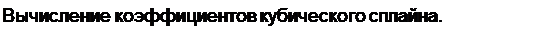
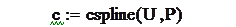
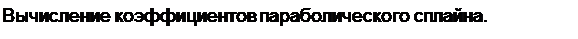
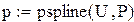
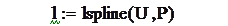
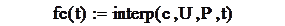
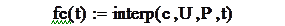
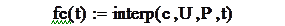
Построим графики этих функций.

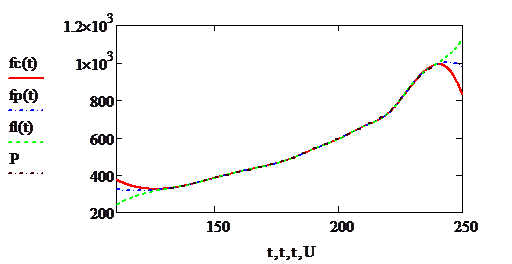
Рис 6.1. Решение примера 6.1 в Mathcad