Источники и классификация погрешностей

Погрешность решения задачи обуславливается следующими причинами:

1) математическое описание задачи является неточным, в частности неточно заданы исходные данные описания;

2) применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций; поэтому вместо точного решения задачи приходится прибегать к приближенному;

3) при вводе данных в машину, при выполнении арифметических операций и при выводе данных производятся округления.

Погрешности, соответствующие этим причинам, называют:

1) неустранимой погрешностью,

2) погрешностью метода,

3) вычислительной погрешностью.

Часто неустранимую погрешность подразделяют на две части:

а) неустранимой погрешностью называют лишь погрешность, являющуюся следствием неточности задания числовых данных, входящих в математическое описание задачи;

б) погрешность, являющуюся следствием несоответствия математического описания задачи реальности, называют, соответственно, погрешностью математической модели

Дадим иллюстрацию этих определений. Пусть у нас имеется маятник (рис. 1.1.), начинающий движение в момент t = t₀ . Требуется предсказать угол отклонения φ от вертикали в момент t₁.

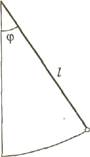
Рис. 1.1. - Маятник

Дифференциальное уравнение, описывающее колебание этого маятника, берется в виде:

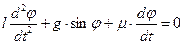, (1.1)

где l — длина маятника, g — ускорение силы тяжести, φ — коэффициент трения.

Как только принимается такое описание задачи, решение уже приобретает неустранимую погрешность, в частности, потому, что реальное трение зависит от скорости не совсем линейно; другой источник неустранимой погрешности состоит в погрешностях определения l, g, µ, t₀, φ(t₀), φ΄(t₀). Название этой погрешности — «неустранимая» — соответствует ее существу, она неконтролируема в процессе численного решения задачи и может уменьшиться только за счет более точного описания физической задачи и более точного определения параметров. Дифференциальное уравнение (1.1) не решается в явном виде; для его решения требуется применить какой-либо численный метод. Вследствие этой причины и возникает погрешность метода.

Вычислительная погрешность может возникнуть, например, из-за конечности количества разрядов чисел, участвующих в вычислениях. Введем формальные определения.

Пусть I — точное значение отыскиваемого параметра (в данном случае — реальный угол отклонения маятника φ в момент времени t₁), II — значение этого параметра, соответствующее принятому математическому описанию (в данном случае — значение φ(t₁) решения уравнения (1.1)),

II_h-— решение задачи, получаемое при реализации численного метода в предположении отсутствия округлений, II_h^*—приближение к решению задачи, получаемое при реальных вычислениях. Тогда

Ρ₁ = II—I — неустранимая погрешность,

Ρ₂ = II_h —I — погрешность метода,

Ρ₃ = II_h^*—II_h — вычислительная погрешность.

Полная погрешность Ρ₀ получается по формуле

Ρ₀= Ρ₁+ Ρ₂+ Ρ₃

Абсолютная и относительная погрешности.

Формы записи данных.

Если а — точное значение некоторой величины а, а * — известное приближение к нему, то абсолютной погрешностью приближенного значения а* называют обычно некоторую величину Δ(а*), про которую известно, что

|а* - а| ≤ Δ(а*)

Относительной погрешностью приближенного значения называют некоторую величину δ(а*), про которую известно, что

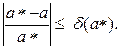
Относительную погрешность часто выражают в процентах. Если а — известное число, например π, то иногда говорят об абсолютной Δ (а) и относительной δ(а) погрешностях задания этого числа: числа Δ(а) и δ(а) называют соответственно абсолютной и относительной погрешностью числа а.

Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.

Пример 1.1. У чисел а* = 0,07045, а* = 0,07045000 значащими цифрами являются подчеркнутые цифры. Число значащих цифр в первом случае равно 4, во втором — 7.

Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пример 1.2. а* = 0,06045, Δ(а*)=0,000003;

а* = 0,06045000, Δ(а*)=0,0000007;

подчеркнутые цифры являются верными.

Уславливаются называть значащую цифру верной в строгом смысле, если абсолютная погрешность не превосходит половины единиц разряда, соответствующих этой цифре.

Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.

Пример 1.3. При а* = 0,03045, Δ(а*)= 0,000003 число а* записано со всеми верными цифрами.

Иногда употребляется термин число верных цифр после запятой: подсчитывается число цифр после запятой от первой цифры до последней верной цифры. В последнем примере это число равно 5.

Довольно часто информация о некоторой величине задается пределами ее измерения:

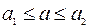, (1.2)

например, .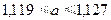

Принято записывать эти пределы с одинаковым числом знаков после запятой, Так как обычно достаточно грубого представления о погрешности, то в числах а₁, а₂ часто берут столько значащих десятичных цифр, сколько нужно, чтобы разность а₁ — а₂ содержала одну-две значащие цифр. Абсолютную или относительную погрешность обычно записывают в виде числа, содержащего одну или две значащих цифры. Информацию о том, что, а* является приближенным значением числа а с абсолютной погрешностью Δ (а*), иногда записывают в виде

а = а*± Δ(а*), (1.3)

числа а* и Δ(а*) принято записывать с одинаковым числом знаков после запятой. Например, записи

а = 1,132 ±0,004, а = 1,132 ±4*10^-3

относятся к общепринятым и означают, что

1,132 - 0,004 < а < 1,132 + 0,004.

Соответственно информацию о том, что а* является приближенным значением числа а с относительной погрешностью (а*), записывают в виде

a = a*(1± δ(a*)). (1.4)

Например, записи

а = 1,132 (1 ± 0,004), а = 1,132(1 ± 4 *10^-3), а = 1,132(1 ± 0,4℅)

означают, что

(1 - 0,004)1,132 < а < (1 + 0,004)1,132.

При переходе от одной из форм записи к другой надо следить, чтобы пределы измерения, указываемые новой формой записи, были шире старых, иначе такой переход будет незаконным. Например, при переходе от (1.2) к (1.3) должны выполняться неравенства

a*- Δ(a*) 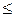a₁, a₂ 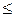a* + Δ(a*),

при переходе от (1.3) к (1.4) — неравенства

а*(1 - δ (а*)) 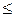а* - Δ (а*), а* + Δ (а*) 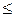а*(1 + δ(а*)),

при переходе от (1,4) к (1.3) должны выполняться противоположные неравенства (пределы всегда расширяются!).

Следует различать принятую нами выше формально математическую и обиходную терминологии в рассуждении о величине погрешности. Если в постановке задачи говорится, что требуется найти решение с погрешностью 10^-2, то чаще всего не имеется в виду обязательность этого требования. Предполагается лишь, что погрешность имеет такой порядок. Если, например, решение будет найдено с погрешностью 2-10^-2, то такой результат, также удовлетворителен.

Вычислительная погрешность

Далее для краткости будем обозначать абсолютную погрешность числа x как Δ_x относительную погрешность как δ_Х .

1. Погрешность суммирования чисел х±Δ_х, у± Δ_y

Абсолютная: погрешность:

Δ_z = (x± Δ_x)+(y± Δ_y)=(x + y) ±(Δ_x± Δ_y)

Относительная погрешность:

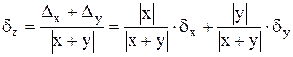
2. Погрешность вычитания чисел х±Δ_х, у± Δ_Y

Абсолютная: погрешность:

Δ_z = (x± Δ_x)-(y± Δ_y)=(x + y) ±(Δ_x± Δ_y)

Относительная погрешность:

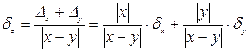
3. Погрешность умножения чисел х±Δ_х, у± Δ_y

Абсолютная: погрешность:

z = (x± Δ_x) (y± Δ_y)=xּy± yּΔ_x ±xּΔ_y± Δ_xּΔ_{y =} xּy± yּΔ_x ±xּΔ_y

Относительная погрешность:

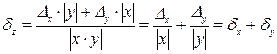
4. Погрешность деления чисел х±Δ_х, у± Δ_y

Абсолютная: погрешность:

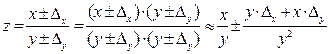
Относительная погрешность:

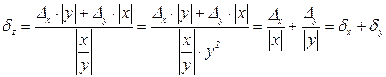
5. Погрешность функции, зависящей от одной переменной.

Абсолютная: погрешность:

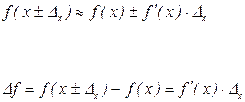
Относительная погрешность:

.
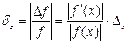