Раздел 1. Элементы комбинаторики.

Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.

Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать k способами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами.

Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно .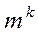

Пример. Имеются цифры 2, 3, 5, 7. Сколько различных четырехзначных чисел можно составить из этих цифр?

Решение. Первой цифрой в числе может быть любая из четырех имеющихся. То же самое можно сказать и о последующих цифрах числа, поэтому общее число комбинаций: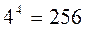

Размещение без повторений. Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из k элементов (k£m), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из m элементов по k элементов, а их общее число можно выразить формулой .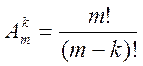

Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются?

Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4: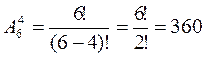

Перестановки. Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно: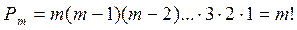

Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются?

Решение. Количество чисел равно числу перестановок из четырех элементов: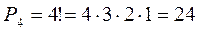

Сочетания. Пусть из множества, содержащего m различных элементов, требуется выбрать подмножество, содержащее k различных элементов (k £ m). Получаемые при этом подмножества не упорядочены. Такие неупорядоченные подмножества называются сочетаниями. Число сочетаний из m элементов по k элементов вычисляется по формуле: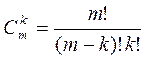

Пример. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?

Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: .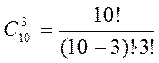

Теоретические вопросы к разделу 1.

1. Сформулировать правило произведения.

2. Указать формулы для подсчета числа размещений при выборке с повторениями и без повторений.

3. Записать формулы для подсчета числа сочетаний.

Задание к разделу 1.

1. В группе 20 студентов. Сколькими способами можно выбрать троих студентов для участия в конференции?

2. В группе 24 студентов. Требуется выбрать старосту и профорга. Сколькими способам можно это сделать?

3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?

4. Сколько можно составить трехзначных чисел из цифр 1, 2, 3, 4, 5, 6, 7, 8. 9, если все цифры, входящие в одно и то же число, различные?

5. Сколькими способами четыре человека могут разместиться за круглым столом?

6. Сколько различных слов, каждое из которых содержит 4 буквы, можно составить из букв слова ВЫБОРКА? (Под словом понимаем любой набор букв.)

7. Электрическая цепь имеет 6 переключателей. Каждый переключатель может быть включен или выключен. Сколько существует различных положений, в которых могут оказаться все переключатели?

8. Сколько четырехзначных чисел можно образовать из нечетных цифр, если каждая из этих цифр в числе может повторяться?

9. В бригаде 8 человек. Для проведения работ требуется группа из четырех человек. Сколькими способами можно составить такую группу работников?

10. Имеется 6 билетов в театр, 4 из которых на места из первого ряда. Сколькими способами можно выбрать из шести имеющихся билетов три так, чтобы два билета оказались на места первого ряда, а один билет – на место в другом ряду?