Изучение дифракции света в сходящихся лучах (дифракция френеля)

Цель работы: изучение дифракционных явлений при распространении сферической световой волны через круглое отверстие в непрозрачном экране.

Приборы и принадлежности: источник света – газовый (He-Ne) лазер, оптическая скамья с сантиметровой шкалой, собирающая линза, диафрагма, отражающий экран, фотоэлемент, микроамперметр.

Введение

При распространении света в среде с резкими неоднородностями наблюдается явление дифракции, то есть нарушение законов геометрической оптики, приводящее к отклонению распространения света от прямолинейного вблизи краев непрозрачных тел. Данное явление обусловлено волновой природой света. В случае, когда дифракция наблюдается в сходящихся (непараллельных) лучах, говорят о дифракции Френеля.

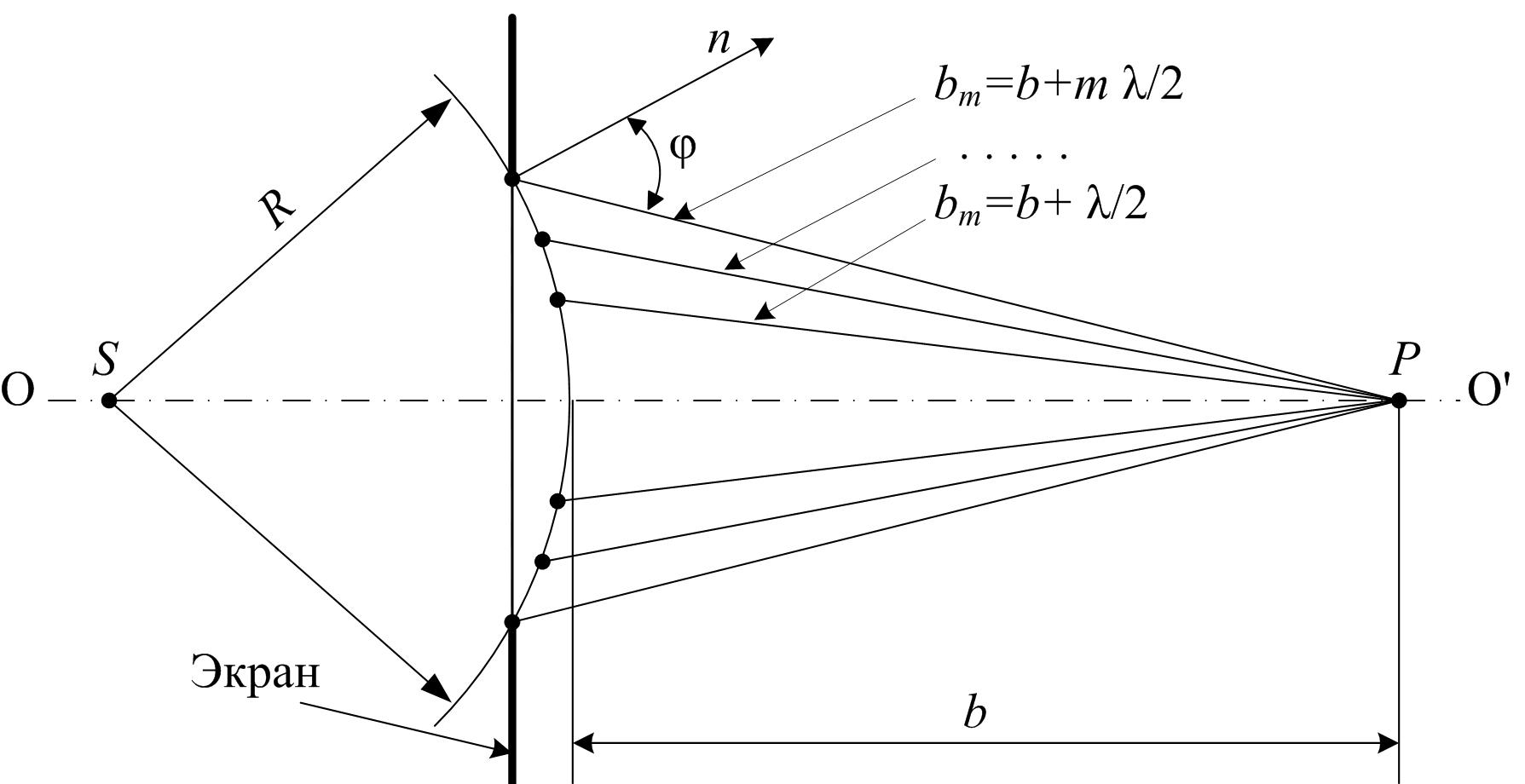
Рис. 1

Рассмотрим дифракцию Френеля на примере распространения сферической световой волны через круглое отверстие в непрозрачном экране. Для того, чтобы определить действие световой волны в какой-либо точке Р на линии ОО' (рис. 1), воспользуемся методом зон Френеля. Разобьем открытую волновую поверхность на кольцевые зоны Френеля, построенные таким образом, чтобы расстояние от краев соседних зон до точки Р отличалось на половину длины волны λ/2.

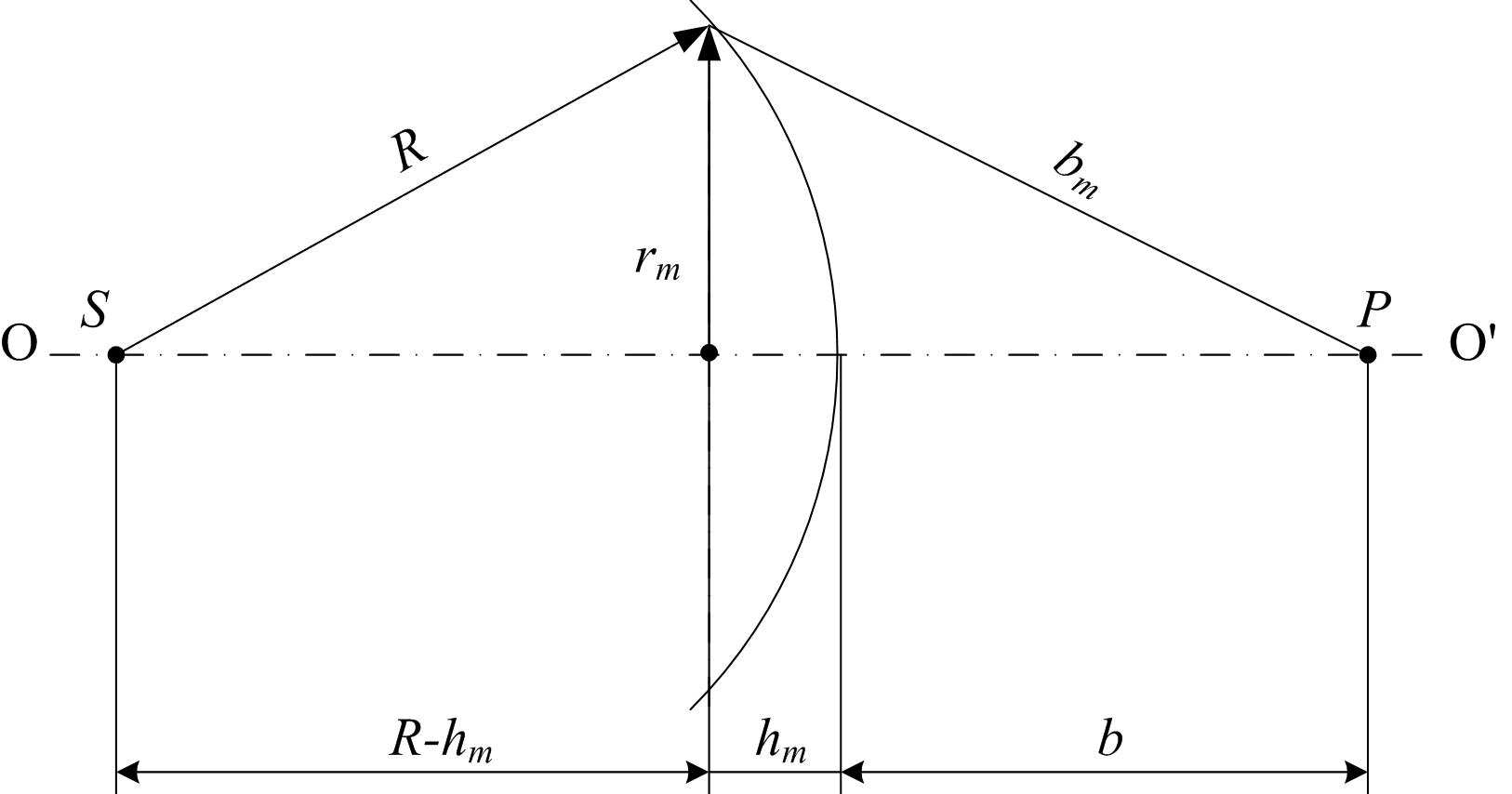
Рис. 2

Определим площади и радиусы зон Френеля. Согласно рис. 2, имеет место соотношение

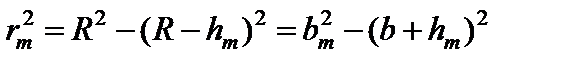, (1)

где r_m – радиус зоны Френеля под номером m;

R – радиус волновой поверхности;

h_m – высота сферического сегмента, выделяемого внешней границей m-й зоны;

b – расстояние от волновой поверхности до точки наблюдения P;

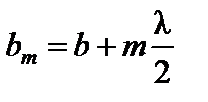– расстояние от точки P до границы зоны Френеля под номером m.

Ввиду малости λ при небольших значениях m можно пренебречь слагаемым, содержащим λ². С учетом этого приближения из формулы (1) следует

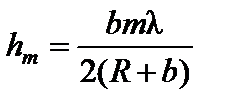(2)

Так как площадь сферического сегмента S_m = 2pR h_m, выражение для площади m-й зоны имеет вид

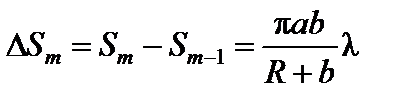. (3)

Следовательно, площади зон Френеля примерно одинаковы (ΔS_m не зависит от m).

Полагая h_m << R, из соотношения (1) получим для радиуса зоны Френеля под номером m выражения r_m =2Rh_m, или с учетом (2),

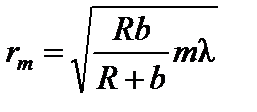. (4)

Очевидно, если r_m является одновременно радиусом r рассматриваемого отверстия в экране, то оно открывает часть волнового фронта, на котором умещается число зон Френеля, равное

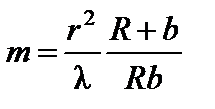. (5)

Интенсивность света в точке наблюдения Р зависит от числа m открытых зон Френеля. Колебания, возбуждаемые в точке Р вторичными источниками от аналогичных участков соседних зон, будут находиться в противофазе, то есть ослаблять друг друга (по определению расстояния до указанных участков от точки Р отличаются на λ/2). Следовательно, если отверстие открывает четное число зон Френеля, в точке Р наблюдается минимум освещенности, нечетное – максимум.

Амплитуды колебаний, возбуждаемых зонами в точке Р, в соответствии с принципом Гюйгенса-Френеля образуют монотонно убывающую последовательность

A₁ > А₂ > . . . > A_m-1 >A_m > A_m+1 > . . .

Это связано с тем, что площади зон примерно одинаковы, а расстояния b_m от зоны до точки наблюдения Р увеличиваются с ростом m. Кроме того, от центральной зоны к периферическим увеличивается угол j между нормалью к элементам зоны и направлением на точку Р (см. рис. 1). Амплитуда результирующего колебания равна алгебраической сумме амплитуд:

A = A₁- A₁+ A₃- A₄+ . . . (6)

Здесь знак минус учитывает, что фазы колебаний, возбуждаемые соседними зонами, отличаются на p.

Преобразуем выражение (6) к виду

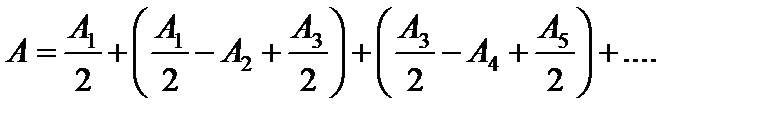(7)

Вследствие монотонного убывания А_m можно приближенно считать, что 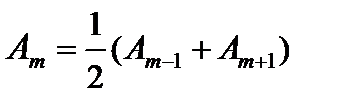. Тогда выражения в скобках будут равны нулю, и амплитуда колебания в точке Р, возбуждаемого полностью открытым волновым фронтом, окажется равной А = A₁/2. Если отверстие открывает только одну центральную зону Френеля, то амплитуда колебания равна А = А₁, то есть в два раза больше. Соответственно интенсивность I в точке Р (которая пропорциональна квадрату амплитуды) при одной открытой зоне в четыре раза больше, чем при полностью открытом волновом фронте так как I ~ А² [2].

Как следует из соотношения (5), при фиксированных длине волны излучения λ, размерах отверстия r и расстоянии между источником света S и точкой наблюдения Р освещенность в точке Р будет зависеть от положения экрана – расстояний R и b.

Описание установки

Схема установки приведена на рис. 3. На одном конце оптической скамьи располагается источник света – (He-Ne) лазер 1, дающий монохроматическое излучение с длиной волны λ = 0,628 мкм (рис. 3). Луч лазера с помощью собирающей линзы 2 фокусируется в точку S и далее распространяется в виде сферической волны. На некотором расстоянии от точки S располагается рейтер 3 с ирисовой диафрагмой так, что ее центр совпадает с оптической осью установки.

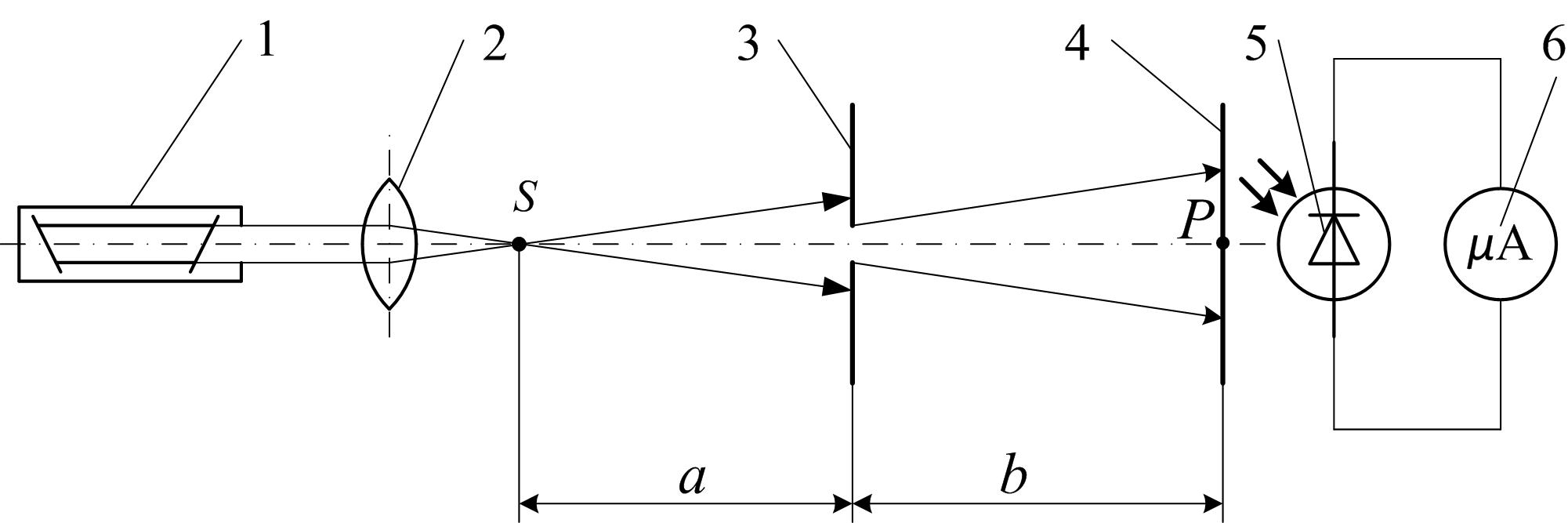
Рис. 3

Диафрагма представляет собой круглое отверстие переменного диаметра. Диаметр отверстия регулируется поворотом рычага диафрагмы. На другом конце оптической скамьи помещается экран 4 для наблюдения дифракционной картины и фотоэлемент 5, предназначенный для измерения освещенности. Сила тока в цепи фотоэлемента пропорциональна интенсивности света, и может быть измерена с помощью микроамперметра 6 (mA).

Для измерения расстояния между диафрагмой и точечным источником S используется сантиметровая шкала оптической скамьи, начало отсчета, которой совпадает с положением источника сферической волны.

Порядок выполнения работы

Задание 1. Определение отношения интенсивностей света в точке Р

1.1. Включить блок питания лазера. После появления генерации излучения установить номинальное значение тока накачки (указано на приборе).

1.2. Проверить юстировку оптической схемы: центр отверстия диафрагмы должен совпадать с осью симметрии расходящейся сферической волны.

ВНИМАНИЕ! Устранение неточностей юстировки выполняется только дежурным лаборантом.

1.3. Перемещая экран 4 вдоль направляющего рельса, установить его на пути оптического излучения.

1.4. Поместить рейтер с диафрагмой 3 на одинаковом расстоянии L от точечного источника света S и экрана. В этом случае R = b = L и, согласно формуле (5), имеет место равенство

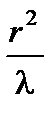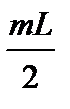= (8)

1.5. Медленно вращая кольцо диафрагмы, изменять величину отверстия и наблюдать на экране за изменениями дифракционной картины. По виду дифракционной картины (рис. 4) [2] определить, в каком случае в отверстии укладываются ровно одна зона Френеля, две и т. д. (K = 1; K = 2; ...).

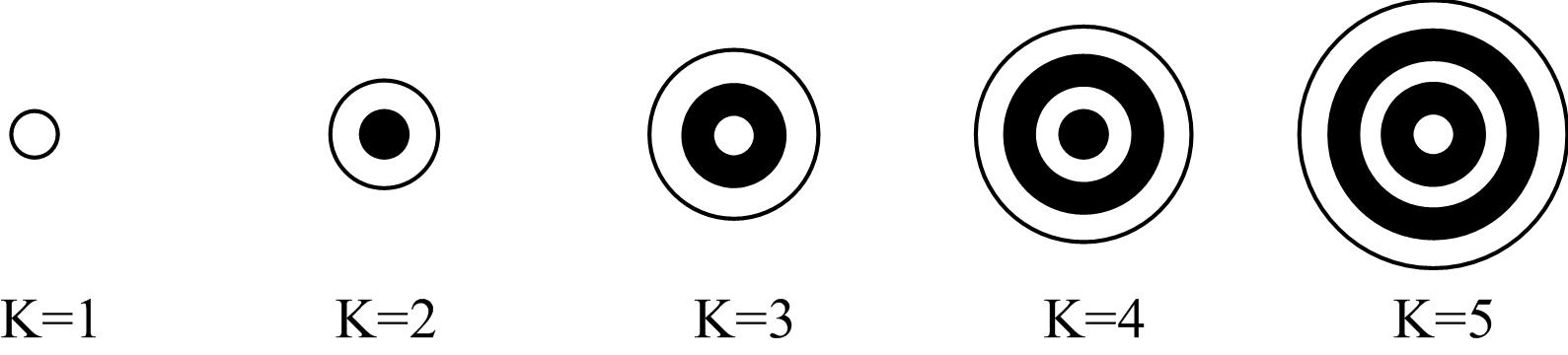
Рис. 4

Таблица 1

Число открытых зон Френеля	Величина фототока, мкА	Отношение интенсивностей света.
m = 1	i1 =	= =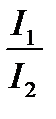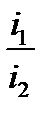
m >> 1	i2 =

1.6. Поворотом кольца диафрагмы установить размер отверстия, при котором на экране наблюдается дифракционная картина, соответствующая одной открытой зоне Френеля (яркая точка).

1.7. Установить рейтер с фотоприемником 5 так, чтобы поток света попадал на фотоэлемент. Включить микроамперметр, установив переключатель диапазонов в положение μA.

Для более точной юстировки оптической схемы слегка повернуть кольцо диафрагмы вправо-влево, добившись максимального значения фототока на экране микроамперметра. Записать полученное значение фототока i₁ в таблицу 1.

Убрать рейтер с диафрагмой, полностью открыв волновой фронт. Записать полученное при этом значение фототока i₂в таблицу 1 и найти отношение i₁/i₂. Сравнить его с теоретическим, считая, что значение фототока пропорционально интенсивности света I в точке Р.

Выключить микроамперметр, вернуть в исходное положение экран и рейтер с диафрагмой.

Задание 2. Экспериментальная проверка формулы (5) для числа m зон Френеля, открываемых отверстием радиуса r

2.1. Не меняя размера отверстия диафрагмы, медленно перемещать диафрагму 3 в сторону точечного источника света S и наблюдать за изменением дифракционной картины. По виду дифракционной картины (см. рис. 4) определить расстояния a между точечным источником S и диафрагмой, при которых в отверстии укладываются ровно две, три и четыре зоны Френеля. Расстояния R измеряются линейкой и заносят в таблицу 2.

2.2. Рассчитать указанные расстояния a теоретически по формуле

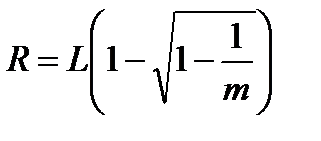, (9)

которая следует из (5), где вместо r²/λвзята величина L/2 (смотри соотношение (8) при m = 1), а расстояние b = 2L - R.

Полученные значения занести в таблицу 2 и сравнить с экспериментальными значениями.

Таблица 2.

Число открытых зон Френеля, m	Расстояние a, см
Экспериментальное	Теоретическое

2.3. Сделайте заключение по результатам работы.

Контрольные задания

1. Что называется дифракцией света?

2. В чем состоит сущность метода зон Френеля?

3. Выведите формулы для определения радиусов и площадей зон Френеля.

4. Зависит ли площадь зон Френеля от номера зоны?

5. Как зависит интенсивность света в точке P от числа открытых зон Френеля?

6. Как меняется дифракционная картина, если при данных r и R увеличивать расстояние от отверстия до экрана?

7. Каково соотношение между интенсивностями света в точке P в случаях, когда отверстие открывает одну зону Френеля и при полностью открытом волновом фронте?

Список литературы

1. Савельев И.В. Курс физики. М.: Наука, 1989.-Т.3.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Изд-во «Академия», 2003. – 720 с.

3. Ландсберг Г.С. Оптика. Учебное пособие: Для вузов. – 6-е изд., стереотип. – М.: Физматлит, 2003. – 848 с.

Работа 303

Изучение явления дифракции света в параллельных лучах (дифракция Фраунгофера)

Цель работы: изучение дифракции света при падении плоской когерентной монохроматической волны на щель в непрозрачном экране и нить; использование дифракционных явлений для определения длины волны света и неконтактного измерения толщины нити.

Приборы и принадлежности: источник света газовый (He-Ne) лазер, щель регулируемой ширины, нить, матовый экран с горизонтальной миллиметровой шкалой, линейка.

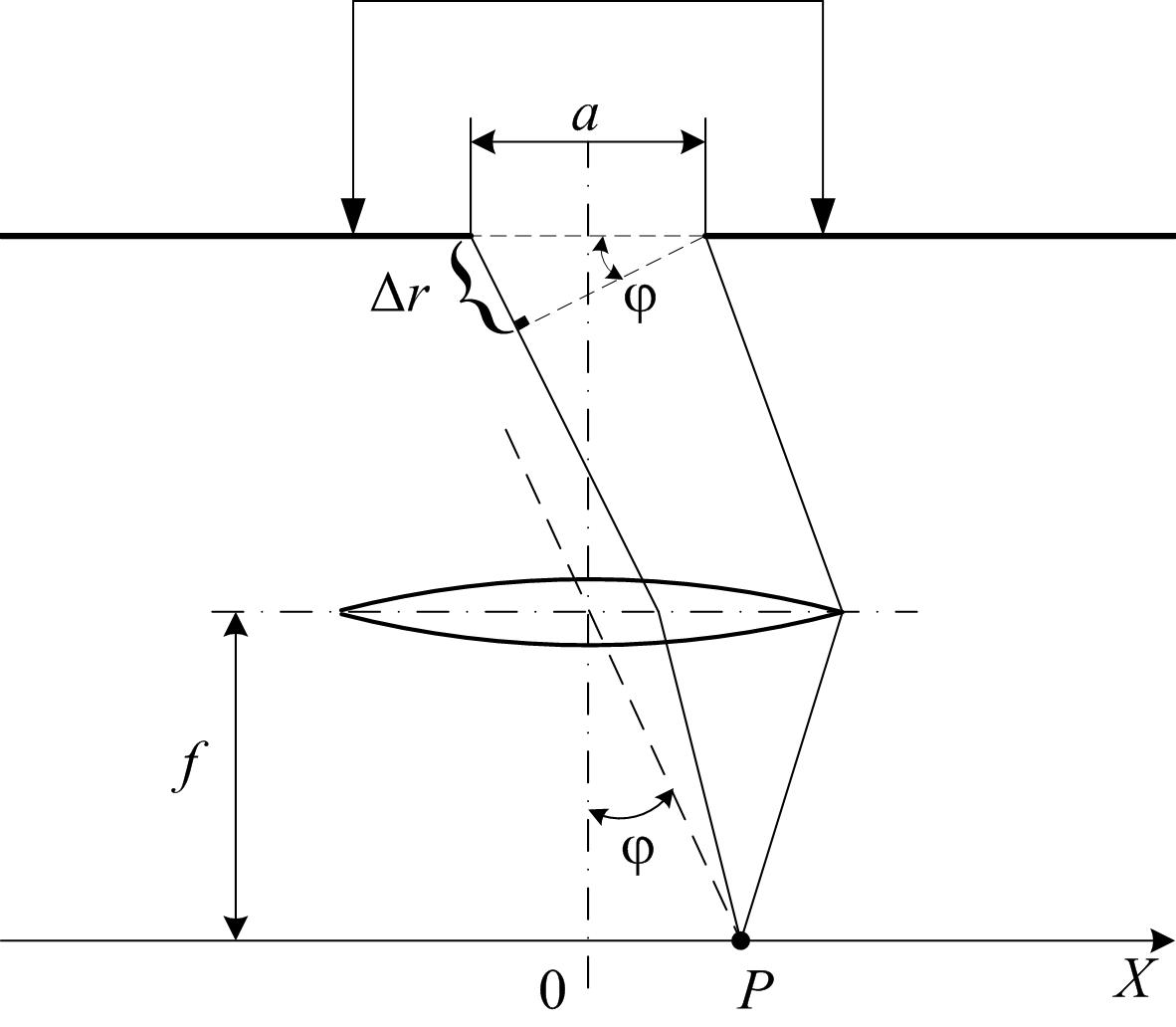
Рис. 1.

Рассмотрим дифракцию света (определение явления дифракции см. [2] при падении плоской когерентной монохроматической волны на длинную щель в непрозрачном экране (рис. 1). Пусть свет падает на щель нормально к ее поверхности, так что колебания в плоскости щели совершаются в одной фазе. Для того, чтобы наблюдать дифракцию Фраунгофера, точку наблюдения Р необходимо расположить на достаточно большом расстоянии, где лучи, идущие от краев щели в точку Р, будут практически параллельными. Это условие легко реализовать, поместив за щель собирающую линзу так, чтобы точка наблюдения Р находилась в фокальной плоскости линзы (линза собирает в фокальной плоскости в одной точке параллельные лучи).

Решим задачу о дифракции Фраунгофера на щели, используя метод графического сложения амплитуд. Для этого разобьем открытую часть волновой поверхности на узкие полоски одинаковой ширины а₀ параллельные краям щели. Колебания, возбуждаемые каждой такой плоскостью в точке наблюдения Р, имеют одинаковую амплитуду А₀ и отстают по фазе от предыдущего колебания на величину

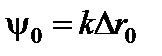, (1)

где k = 2p/l – волновое число;

λ – длина волны;

Dr₀ = а₀sinj – разность хода лучей, приходящих в точку Р от соседних полосок;

j – угол дифракции, определяющей направление на точку P.

Соответственно разность фаз между лучами, идущими в точку Р от краев щели, будет равна

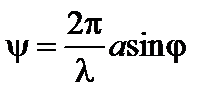, (2)

где а – ширина щели.

При выводе соотношений (1) и (2) учитывалось, что линза не вносит дополнительной разности хода лучей. Для определения результирующей амплитуды колебания удобно использовать векторные диаграммы. С этой целью амплитуде колебания, возбуждаемого m-й полоской в точке Р. ставится в соответствие вектор А_m, модуль которого равен A₀, а направление задается таким образом, чтобы угол между векторами А_т и А_т-1 отличался на y₀. Векторная диаграмма (рис. 2.) иллюстрирует сложение векторов А_m и позволяет найти результирующий вектор, модуль которого равен амплитуде A результирующего колебания в точке Р. При j = 0 разность фаз y₀ = y = 0.

Если y = p, колебания от краев щели находятся в противофазе. Соответственно векторы А_m располагаются вдоль полуокружности (см. рис. 2.) длиной L. Результирующая амплитуда при этом оказывается равной диаметру полуокружности и может быть найдена из равенства

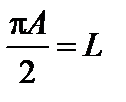, откуда .

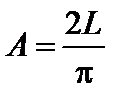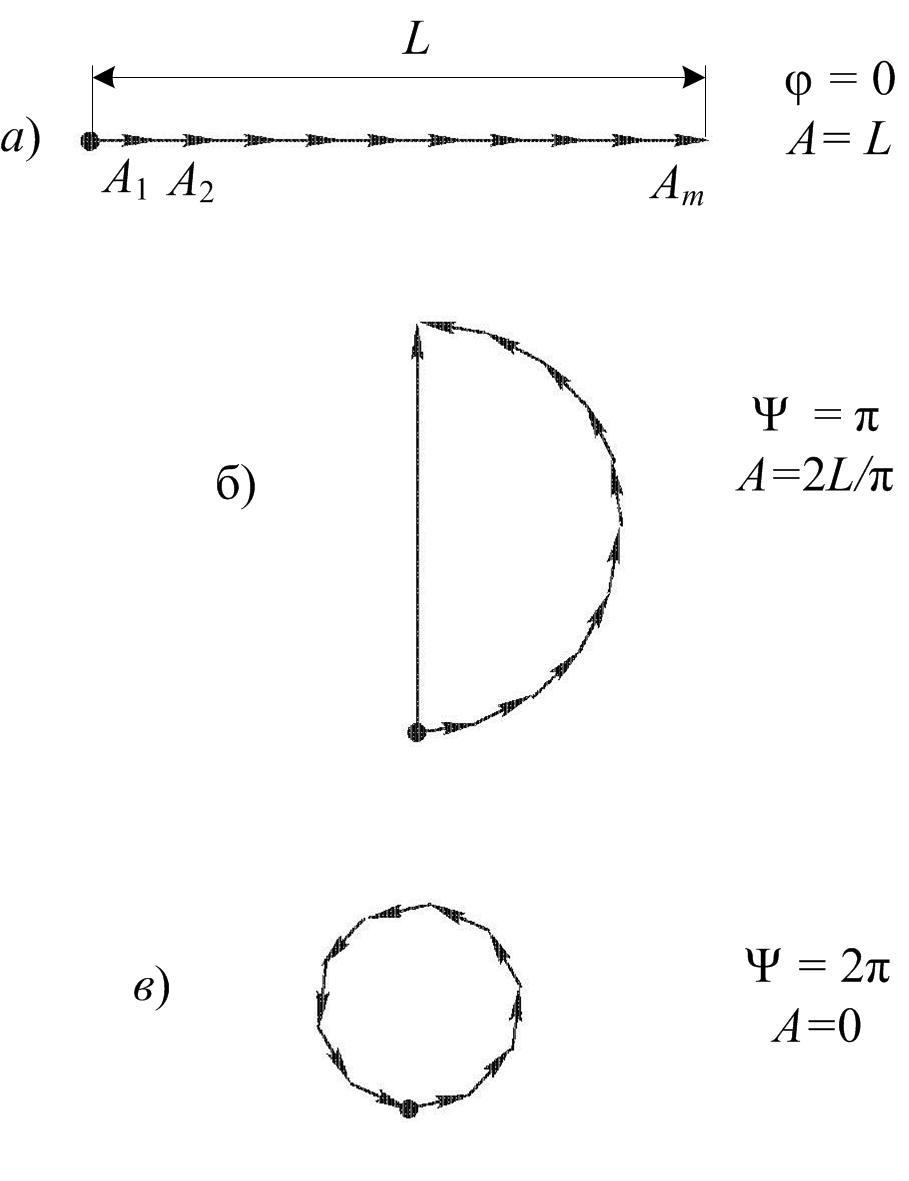
Рис. 2.

В случае y = 2p, (рис. 2.) векторы А_m располагаются вдоль окружности длиной L. Результирующая амплитуда равна нулю – получается первый минимум. Первый максимум получается при y = 3p,. Найдем его амплитуду.

,

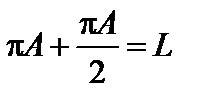следовательно:

.

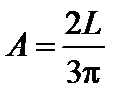Продолжая аналогичные построения, можно прийти к выводу, что дифракционная картина представляет собой чередование максимумов и минимумов интенсивности света, причем интенсивность n-го максимума ослабевает от центра дифракционной картины к её краям в следующем соотношении [3]:

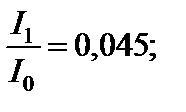
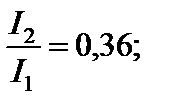
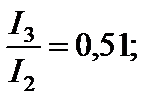
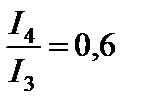и т. д.

Условие образования n-го минимума дифракционной картины Фраунгофера может быть записано в виде:

y = ±2np,

где n = 1, 2, 3, ….., или, с учетом выражения (2),

аsinj = ±nl.(3)

Как следует из рис. 1,

,

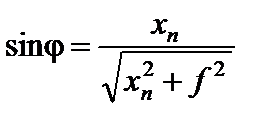где х_n – координата n-го минимума в плоскости наблюдения,

f – фокусное расстояние линзы.

При условии f >> х_n

,

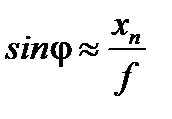следовательно, имеет место равенство

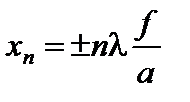. (4)

При переходе от n-го минимума к (n + 1-му) координата x точки Р изменяется на величину

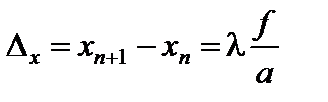. (5)

Расстояние ∆_x, таким образом, определяет ширину дифракционной полосы. Зная D_x, f и a, по формуле (5) можно определить длину волны света l, а при известных l, f и ∆_x – ширину щели a (или нити) [3].

Описание установки

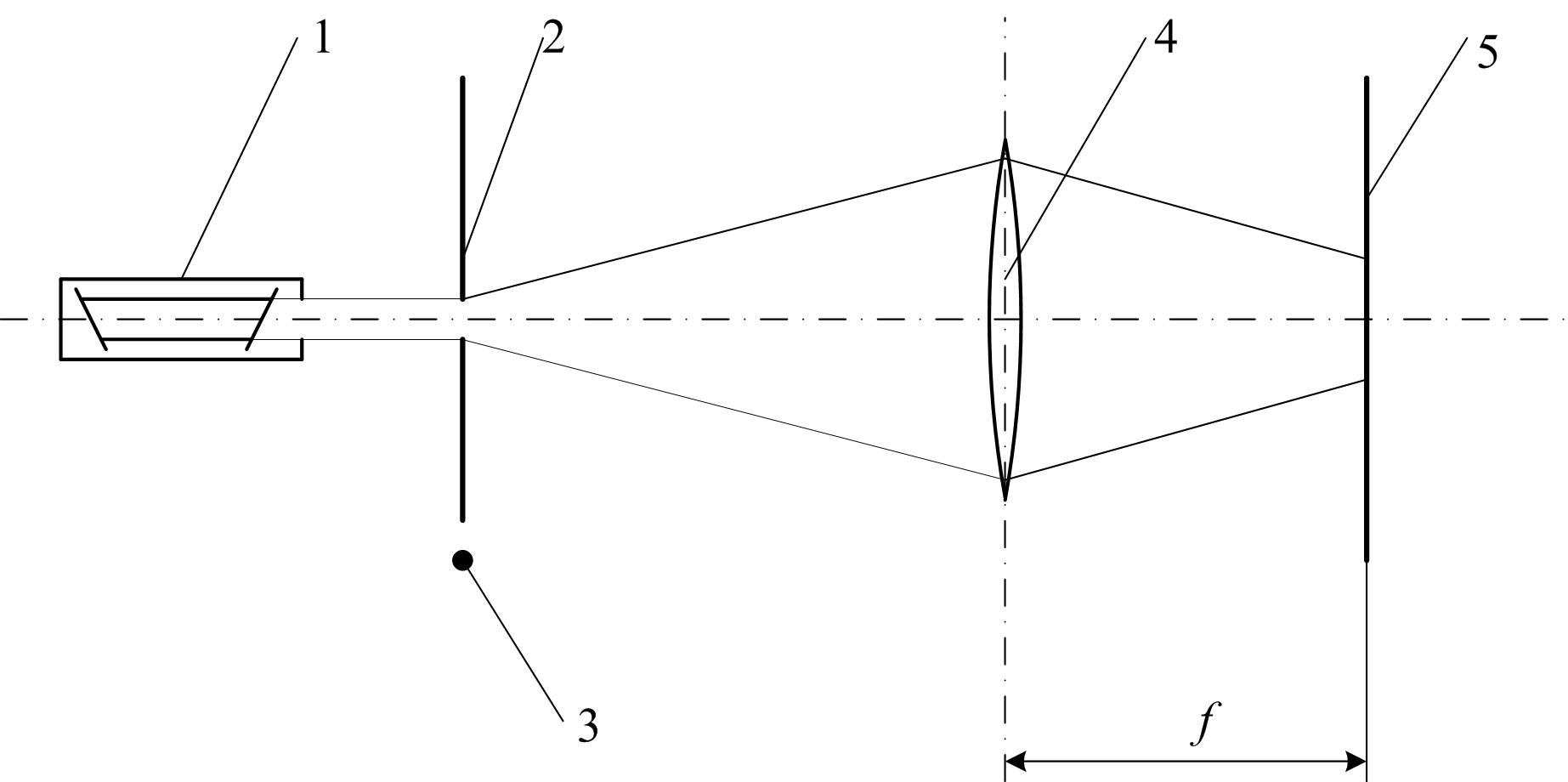
Рис. 3.

В качестве источника когерентного монохроматического света используется газовый (He-Ne) лазер 1 (рис. 2). На пути лазерного луча устанавливаются рейтеры с щелевой диафрагмой 2 или нитью 3, которые могут перемещаться вдоль направляющего рельса. Ширина щели регулируется микрометрическим винтом с точностью до 0,01 мм. Дифракционная картина наблюдается на экране 5, расположенном во фронтальной плоскости линзы 4. Экран снабжен подвижной риской и миллиметровой шкалой, предназначенными для измерения ширины дифракционных полос.

Порядок выполнения работы