ЧОУ ВПО «Южно-Уральский институт управления и экономики»

ЧОУ ВПО «Южно-Уральский институт управления и экономики»

МАТЕМАТИКА

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ № 2

ПО РАЗДЕЛУ «МАТЕМАТИЧЕСКИЙ АНАЛИЗ»

ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

Челябинск, 2015

СОДЕРЖАНИЕ

Введение…………………………………………………………………………….
Методические рекомендации по изучению тем курса………………………….
Методические рекомендации по выполнению контрольной работы …………
Задания для домашней контрольной работы…………………………………
Перечень вопросов для подготовки к промежуточной аттестации……………
Рекомендуемая литература……………………………………..........................
Приложение А. Образец оформления титульного листа………………………
Приложение Б. Образец оформления карточки рецензента…………………….

ВВЕДЕНИЕ

Цель курса математики в системе подготовки специалиста – освоение необходимого математического аппарата для решения профессиональных задач.

Задачи изучения математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке умения моделировать реальные процессы.

В результате изучения математики (часть 2) студент должен:

знать:

- основные понятия и методы математического анализа;

уметь:

- решать типовые математические задачи, что необходимо для анализа, моделирования и решения прикладных экономических задач, в том числе с использованием ЭВМ.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ИЗУЧЕНИЮ ТЕМ КУРСА

Раздел I. Введение в анализ.

Тема 1. Функции

Понятие о множествах. Действительные числа и числовые множества. Постоянные и переменные величины. Функции и способы их задания. Область определения функции. Четные, нечетные, монотонные и ограниченные функции. Сложная функция. Понятие элементарной функции. Основные элементарные функции и их графики. Неявные функции. ( гл. 4, § 4.1 – 4.3, 4.6; с. 95 – 99, 100 – 103,.115 – 117); (2, гл. 5,4).

Прежде всего, полезно ознакомиться с некоторыми логическими символами и кванторами, чтобы использовать их в дальнейшем для сокращения записей (1, с. 123).

Изучение темы следует начать с основных понятий теории множеств , [1, с. 123 – 124]. Далее нужно четко усвоить важнейшее понятие математического анализа – функции, уметь находить область ее определения, знать три способа задания функции: аналитический, графический, табличный.

Студенту нужно знать простейшие преобразования для построения функций: сдвиг графика y=f(x+a)+b вправо при а < 0 и влево при a > 0, а также на 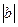параллельно оси Ох вниз при b< 0 и вверх на 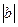при b >0; сжатие 0<m<1 (растяжение m >1) графика функции y=m×f(x) вдоль оси Ох.

В курсе рассматриваются в основном элементарные функции. Студент должен уяснить определение элементарной функции (1, с. 132) четко знать свойства и строить графики следующих основных элементарных функций: у = С (постоянная), у = xⁿ (степенная), у =a^x (показательная), у =log_ax (логарифмическая). Необходимо усвоить понятие сложной функции (функции от функции).

Построение графика четной (нечетной) функции можно значительно упростить, если учесть, что графики четных функций симметричны относительно оси Оу, а нечетных – относительно начала координат. Одним из характерных свойств функции является монотонность (т.е. возрастание или убывание на каком-либо промежутке).

Студенту необходимо уяснить, что функции находит широкое применение в экономической теории. Знать конкретные виды функций и их сущность (функция полезности, функция издержек и т.д.).

Рекомендуется разобрать задачи с решениями N4.1 – 4.3, 4.5, 4.10, 4.12 и задачи для самостоятельного решения N 4.14 – 4.19, 4.21 – 4.23 по учебнику (1) и аналогичные задачи по практикуму (2).

Тема 2. Пределы и непрерывность

Предел числовой последовательности. Предел функции в бесконечности и точке. Бесконечно малые величины и их свойства. Бесконечно большие величины. Основные теоремы о пределах: теорема единственности, предел суммы, произведения, частного. Признаки существования предела. Второй замечательный предел. Число е. Понятие о натуральных логарифмах. Непрерывность функции в точке и на промежутке. Основные теоремы о непрерывных функциях. Вычисление пределов. (1, гл.6, § 6.1–6.7); (2, гл.6).

Необходимо ознакомиться с определением предела числовой последовательности (1, с.141,142) и его геометрической интерпретацией; понять определение предела функции в точке (1, с.143–146) и в бесконечности и познакомиться с их геометрической интерпретацией.

Суть предела числовой последовательности в том, что для любого сколь угодно малого положительного числа e>0 можно найти номер числовой последовательности (N=N(e)), что для всех членов последовательности с номерами n>N верно неравенство êa_n-Aê<e.

Весьма важным являются понятия бесконечно малых и бесконечно больших величин (1, с.147—153), суть которых сводится к тому, что при своем изменении бесконечно малая (по абсолютной величине) будет меньше любого, сколь угодно малого числа e<0, а бесконечно большая будет больше любого сколько угодно большого числа М>0.

Нужно знать взаимосвязь бесконечно больших и бесконечно малых величин, с помощью которых доказываются теоремы о пределах. Следует обратить внимание на признаки существования пределов, особенно на теорему 1 (1, с.155), часто позволяющую установить наличие предела значительно проще, чем при использовании его определения.

Необходимо (без вывода) знать второй замечательный предел в двух формах запис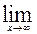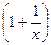и: = e и 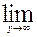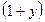^1/y=e.

Понятие непрерывности функции (в точке, на промежутке) является более простым, чем предел, так как оно выражается непрерывностью графика при прохождении данной точки, данного промежутка (без отрыва карандаша от листабумаги). Наряду с интуитивным представлениемнадо знать определение непрерывности функции в точке и на промежутке, свойства непрерывных функций (1, с. 161 – 166), а также то, что всякая элементарная функция непрерывна в каждой точке области определения и может иметь разрыв лишь на границах области определения.

Необходимо ознакомиться с теоретическими вопросами и дать на них ответы.

Рекомендуется разобрать задачи с решениями N6.1-6.3, 6.5, 6.6, . 6.8, 6.9-6.11, 6.13, 6.14 и задачи для самостоятельной работы N 6.18, 6.20 – 6.27, 6.33 – 6.36, 6.38 – 6.41 по учебнику (1) и аналогичные задачи по практикуму (2).

Тема 3. Производная

Задачи, приводящие к понятию производной. Производная, ее геометрический, механический и экономический смысл. Уравнение касательной к плоской кривой; Дифференцируемость функции. Связь между дифференцируемостью и непрерывностью функции (необходимый признак дифференцируемости). Основные правила и основные формулы дифференцирования. Производная сложной функции Производные высших порядков. (1, гл. 7, § 7.1 – 7.7, с. 176 – 205); (2, гл. 7).

Необходимо изучить задачи, приводящие к понятию производной: задачи о касательной и задачи о скорости движения (1, с.176, 177), задачи о производительности труда (экономический смысл производной).

После этого нужно усвоить определение производной как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю. Нужно знать обозначение производной, алгоритм ее вычисления, основываясь на теории пределов.

Студент обязан понимать геометрический и механический смысл производной (1,с.178, 181), уметь решать простейшие задачи по вычислению производной на основе алгоритма ее вычисления; знать и уметь применять основные правила дифференцирования, вычислять производную сложной и обратной функций. При этом нужно знать четко правила вычисления элементарных функций (1,с. 188,193), знать наизусть таблицу производных (1, с.192). Это позволит усвоить дифференцирование сложных функций, обратных функций, неявно заданных функций (1,с.193), находить производные от произведения, суммы, разности, а также вычислять производные высших порядков. Нужно знать использование понятия производной в экономике, понятие эластичности функции, свойства эластичности функции.

Изучая материал этой темы, студенты знакомятся с необходимым условием дифференцируемости функции. Необходимо четко уяснить, что из дифференцируемости функции в некоторой точке следует ее непрерывность в этой точке. Обратная теорема несправедлива, так как существуют непрерывные функции, которые в некоторых точках могут не иметь производной (1, с. 179, 180).

Рекомендуется разобрать задачи с решениями N 7.1 – 7.8, 7.10, 7.13, 1.15 – 7.17 и задачи для самостоятельной работы N 7.20 – 7.29, 7.35, 7 42, 7.43, 7.46 – 7. 49 по учебнику (1) и аналогичные задачи по практикуму (2).

Для усвоения темы нужно решить задачи контрольной работы, ответить письменно на теоретические вопросы в контрольной работе.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ

ВАРИАНТ №1

Задание №1.Вычислить пределы: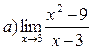

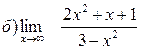
Задание №2.Найти производные функций:

а) 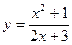б)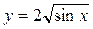

Задание №3. Найти уравнение касательной, проведенной к графику функции у = х³-3х + 5 в точке х₀ = 2.

Задание №4.Исследовать функцию с помощью производных и построить график:

у=2х³ + 3х² + 1

Задание №5. Найти точки экстремума функции нескольких переменных:

z = х² +ху + у² – 2х – 3у.

Задание №6.Найти интегралы:

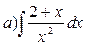
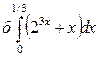
Задание №7.Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной линиями:

у = -х² + 2х; у = 0.

Задание №8.Решить дифференциальное уравнение:

х²dу = у²dх, если при х = 1; у = 1.

Задание №9. Зависимость между издержками производства у и объёмом выпускаемой продукции х на предприятии выражается функцией у = 50х – 0,05х³. Найти средние и предельные издержки при объёме продукции 10 ед.

ВАРИАНТ №2

Задание №1.Вычислить пределы: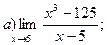

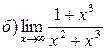
Задание №2.Найти производные функций:

а) 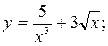б)

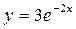
Задание №3.Найти уравнение касательной, проведенной к графику функции 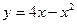в точке .

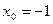Задание №4.Исследовать функцию с помощью производных и построить график:

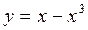
Задание №5. Найтиточки экстремума функции нескольких переменных:

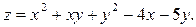
Задание №6.Найти интегралы:

а) 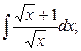б)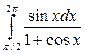

Задание №7.Найти площадь фигуры, ограниченной линиями:

.

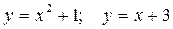Задание №8. Решить дифференциальное уравнение:

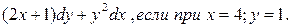
Задание №9.Выручка от продажи конфет составляет р = 50 -0,5х², где х – объём проданной продукции (тыс. ед.) Найти среднюю и предельную выручку, если продано: а) 10 тыс. ед.; б) 60 тыс. ед.

ВАРИАНТ №3

Задание №1.Вычислить пределы: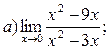

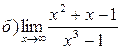
Задание №2.Найти производные функций:

а) 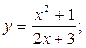б)

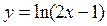
Задание №3.Найти уравнение касательной, проведенной к графику функции

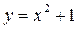в точке .

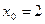Задание №4.Исследовать функцию с помощью производных и построить график:

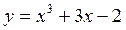
Задание № 5.Найти точки экстремума функции нескольких переменных:

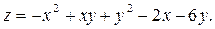
Задание №6. Найти интегралы:

а) 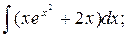б)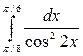

Задание №7.Выполнить чертеж и решить задачу:

Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной линиями: .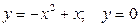

Задание №8. Решить дифференциальное уравнение:

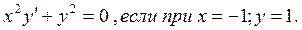
Задание №9.Функция издержек производства у от объёма выпускаемой продукции х имеет вид: у = 100х – 0,2х³. Найти средние и предельные издержки при объёме продукции 10 ед.

ВАРИАНТ №4

Задание №1. Вычислить пределы: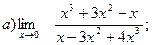

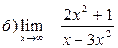
Задание №2.Найти производные функций:

а) 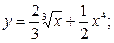б)

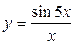
Задание №3.Найти уравнение касательной, проведенной к графику функции 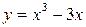в точке .

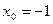Задание№4.Исследовать функцию с помощью производных и построить график:

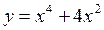
Задание № 5.Найти точки экстремума функции нескольких переменных:

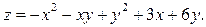
Задание №6.Найти интегралы:

а) 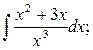б)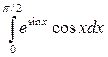

Задание №7.Выполнить чертеж и решить задачу:

Найти площадь фигуры, ограниченной линиями: .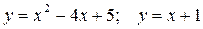

Задание №8. Решить дифференциальное уравнение:

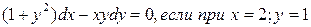
Задание №9. Себестоимость продукции у связана с объёмом выпускаемой продукции х уравнением: у = 6∙ln(1+3x). Найти среднюю и предельную себестоимость выпускаемой продукции при объёме, равном 10 ед.

ВАРИАНТ №5

Задание №1.Вычислить пределы: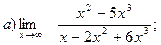

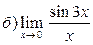
Задание №2.Найти производные функций:

а) 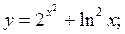б)

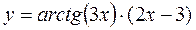
Задание №3.Найти уравнение касательной, проведенной к графику функции 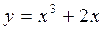в точке .

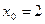Задание№4.Исследовать функцию с помощью производных и построить график:

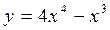
Задание № 5.Найти точки экстремума функции нескольких переменных:

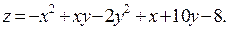
Задание №6.Найти интегралы:

а) 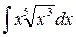б)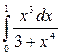

Задание №7. Выполнить чертеж и решить задачу:

Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной линиями: .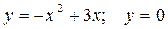

Задание №8.Решить дифференциальное уравнение:

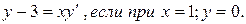
Задание №9. Зависимость между количеством выпускаемых деталей в партии х (тыс. ед.) и затратами на их изготовление у (тыс. руб.) для предприятий отрасли выражается уравнением 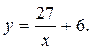Найти эластичность затрат предприятий, выпускающих по 10 тысяч деталей в партии.

ВАРИАНТ №6

Задание №1. Вычислить пределы:

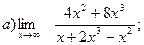
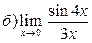
Задание №2.Найти производные функций:

а) 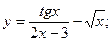б)

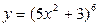
Задание №3.Найти уравнение касательной, проведенной к графику функции

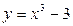в точке .

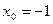Задание№4. Исследовать функцию с помощью производных и построить график:

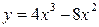
Задание№5.Найти точки экстремума функции нескольких переменных:

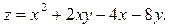
Задание №6.Найти интегралы:

а) 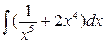б)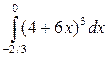

Задание №7.Выполнить чертеж и решить задачу:

Найти площадь фигуры, ограниченной линиями: .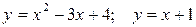

Задание №8.Решить дифференциальное уравнение:

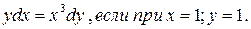
Задание №9. Зависимость между себестоимостью единицы продукции у (в руб.) и выпуском продукции х (в млн. руб.) выражается уравнением у = - 0,5х + 80. Найти эластичность себестоимости при выпуске продукции на 30 млн. руб.

ВАРИАНТ №7

Задание №1. Вычислить пределы: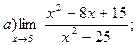

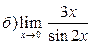
Задание №2.Найти производные функций:

а) 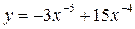б)

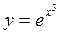
Задание №3.Найти уравнение касательной, проведенной к графику функции 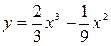в точке .

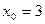Задание№4. Исследовать функцию с помощью производных и построить график:

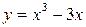
Задание№5.Найти точки экстремума функции нескольких переменных:

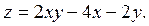
Задание №6.Найти интегралы:

а) 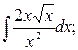б)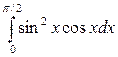

Задание №7.Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной линиями: .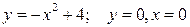

Задание №8.Решить дифференциальное уравнение:

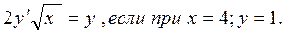
Задание №9.Производительность труда бригады может быть описана уравнением у = - 2,5t² + 15t + 100, где 0 ≤ t ≤ 8 - рабочее время в часах. Вычислить скорость и темп изменения производительности труда при t = 2 и t =7.

ВАРИАНТ №8

Задание №1. Вычислить пределы: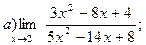

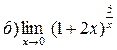
Задание №2.Найти производные функций:

а) 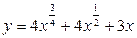б)

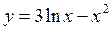
Задание №3.Найти уравнение касательной, проведенной к графику функции 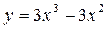в точке .

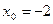Задание№4. Исследовать функцию с помощью производных и построить график:

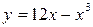
Задание№5.Найти точки экстремума функции нескольких переменных:

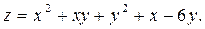
Задание №6.Найти интегралы:

а) 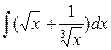б)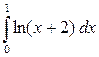

Задание №7.Найти площадь фигуры, ограниченной линиями:

.

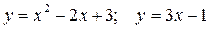Задание №8.Решить дифференциальное уравнение:

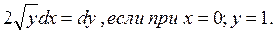
Задание №9.Себестоимость производства телевизоров у (в тыс. руб.) описывается функцией у = 0,01х² – 0,5х + 12, где 5 ≤ х ≤ 50 - объём выпускаемой продукции в месяц (тыс. ед.). Определить скорость и темп изменения себестоимости при выпуске 20 и 40 тыс. ед. продукции.

ВАРИАНТ №9

Задание №1. Вычислить пределы: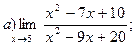

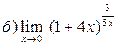
Задание №2.Найти производные функций:

а) 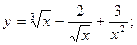б)

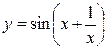
Задание №3.Найти уравнение касательной, проведенной к графику функции 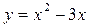в точке .

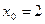Задание№4. Исследовать функцию с помощью производных и построить график:

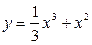
Задание№5.Найти точки экстремума функции нескольких переменных:

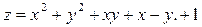
Задание №6.Найти интегралы:

а) 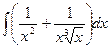б)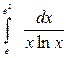

Задание №7.Выполнить чертеж и решить задачу:

Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной линиями: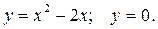

Задание №8.Решить дифференциальное уравнение:

Задание №9.Функция потребления некоторой страны имеет вид:

,

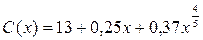где х – совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 32.

ВАРИАНТ №10

Задание №1. Вычислить пределы: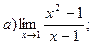

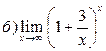
Задание №2.Найти производные функций:

а) 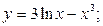б)

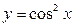
Задание №3.Найти уравнение касательной, проведенной к графику функции 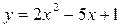в точке .

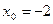Задание№4. Исследовать функцию с помощью производных и построить график:

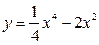
Задание№5.Найти точки экстремума функции нескольких переменных:

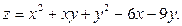
Задание №6.Найти интегралы:

а) 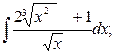б)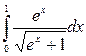

Задание №7.Выполнить чертеж и решить задачу:

Найти площадь фигуры, ограниченной линиями: .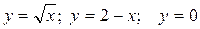

Задание №8.Решить дифференциальное уравнение:

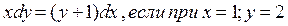
Задание №9.Функция полных затрат в зависимости от объёма выпускаемой продукции задана соотношением: у = х³ – 2х² + 96. При каком объёме производства предельные и средние затраты совпадают? Найти коэффициенты эластичности полных и средних затрат при данном объёме.

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ

ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»,

Литература

1. Н.Ш.Кремер. Высшая математика для экономистов.– М.: Банки и биржи, ЮНИТИ, 2008.

2. Н.Ш.Кремер. Практикум по высшей математике для экономистов.– М.:ЮНИТИ-ДАНА, 2010.

3. И.А.Зайцев. Высшая математика.–М.: Высшая школа, 1998.

Приложение А

Образец оформления титульного листа

ОУ ВО «ЮЖНО-УРАЛЬСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ И ЭКОНОМИКИ»

КОНТРОЛЬНАЯ РАБОТА № 2

ПО ДИСЦИПЛИНЕ: МАТЕМАТИКА

ВАРИАНТ № __

Выполнил студент:

Иванов И.И.

Группа: ТТПЗ-101/03

Дата отправления:

Результат проверки

Проверил преподаватель Баранов И.В.

Дата проверки

Челябинск, 2017 г.

Приложение Б

Образец оформления карточки рецензента

ОУ ВО «ЮЖНО-УРАЛЬСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ И ЭКОНОМИКИ»

КАРТОЧКА РЕЦЕНЗЕНТА

КОНТРОЛЬНАЯ РАБОТА № 2

По дисциплине Математика

Студента Иванова Ивана Ивановича

(фамилия, имя, отчество)

Группа ТТПЗ-101/03 Направление Технология транспортных процессов

Дата проверки «»20год

Оценка

Преподаватель Баранов И.В.

РЕЦЕНЗИЯ

(подпись)

ЧОУ ВПО «Южно-Уральский институт управления и экономики»

МАТЕМАТИКА

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ