Анализ систем массового обслуживания без явных потерь.

До сих пор рассматривались марковские системы, в которых каждая заявка проходила только одну операцию обслуживания. Такие системы можно назвать однофазными. Если заявка получает обслуживание более чем в одном сервере, то говорят о многофазных системах или о сетях массового обслуживания. В общем случае каждый узел такой сети может содержать СМО определенного типа, а заявки могут поступать в сеть в различных точках, и получив обслуживание в одном узле могут поступать на обслуживание в другой для дальнейшей обработки.

При исследовании сети необходимо задавать топологическую структуру сети, так как она определяет возможные переходы заявок между узлами. Требуется также описать маршруты отдельных заявок и вероятностные модели потоков заявок между узлами сети.

Рассмотрим простейшую последовательную систему с двумя узлами (Рис. 1.27).

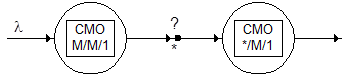
Рис. 1.27 Простейшая последовательная система с двумя узлами

Это топологическая структура сети, а не диаграмма состояний. Предположим, что входной поток пуассоновский с интенсивностью λ, который поступает на первый узел, в котором находится СМО типа M/M/1, с сервером, имеющим показательное распределение времени обслуживания со средним значением μ. Будем считать, что второй узел состоит из единственного обслуживающего прибора с показательным распределением времени обслуживания с интенсивностью также равной μ. Основная задача состоит в вычислении распределения промежутков времени между последовательными заявками, поступающими в узел 2, т.е. уходящими из 1.

Пусть d(t) обозначает плотность распределения вероятностей промежутков между последовательными заявками на выходе узла 1.

Обозначим ее преобразование Лапласа

.

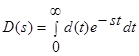Выразим эту функцию через распределение для случая, когда в узле 1 имеется новая заявка т. е. СМО1 не пуста и распределение для случая, когда при уходе заявки из СМО1 на ее входе не было другой заявки т.е. СМО1 пуста. Так как нужно записать преобразование Лапласа для плотности вероятности суммы двух промежутков времени - время до поступления следующего требования и время обслуживания этого требования, и эти два промежутка распределены независимо, то плотность распределения вероятностей их суммы, как известно, равна свертке плотностей распределения вероятностей суммируемых случайных величин. Соответственно преобразование Лапласа плотности распределения суммы равно произведению преобразований исходных плотностей распределения. Тогда преобразование Лапласа плотности вероятности промежутка времени между заявками для случая пустого узла 1 будет:

.

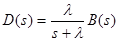Здесь B(s) – преобразование Лапласа плотности вероятности времени обслуживания.

Поскольку время обслуживания является случайной величиной с показательным законом распределения, то:

.

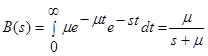Используя то свойство, что вероятность того, что заявка покинет систему пустой, равна вероятности того, что заявка поступит в момент, когда в системе нет заявок и равна в точности 1-ρ. Это позволяет записать преобразование Лапласа для плотности вероятности распределения промежутка времени полностью в виде

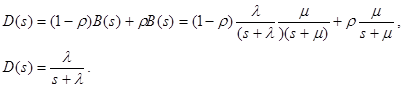
Следовательно, плотность вероятности распределения промежутков времени между заявками, покидающими узел 1, является также случайной величиной с показательным законом распределения с тем же самым параметром. Это значит, что СМО типа М/M/1 превращает пуассоновский поток на входе в пуассоновский поток на выходе с тем же самым параметром. Этот результат называют теоремой Бёрке. Им было показано, что этот факт имеет место для всех СМО типа M/M/m. На основании этой теоремы можно исследовать многофазные последовательностные схемы.

Для произвольной сети массового обслуживания результат получается более сложным и выражается теоремой Джексона.

Рассмотрим сеть (рис.1.28), содержащую N узлов, причем каждый i-й узел состоит из m_i серверов с показательным временем обслуживания с параметром μ_i, в каждый узел извне поступает пуассоновский поток заявок с интенсивностью γ_i. Покидая i-узел, заявка с вероятностью r_ij поступает в j узел.

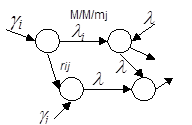
Рис. 1.28 Сеть, содержащая N узлов.

Обозначим λ_i полную интенсивность потока, поступающего в i-й узел, можно показать, что должно выполняться условие баланса

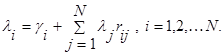
Вероятность, того, что заявка после обслуживания в i-том узле вообще покинет сеть будет равна .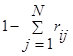

Выполнение условия эргодичности марковской модели каждого узла будет обеспечено, если .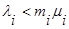

Джексоном было доказано далеко не тривиальноe утверждение, что каждый узел в сети ведет себя так, как если бы он был независимой СМО типа M/M/m с входящим пуассоновским потоком λ_i . В общем случае полный входящий поток не является пуассоновским. Состояние сети с N узлами описывается вектором, компонентами которого являются число заявок в каждом из узлов сети .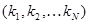

Джексону удалось доказать, что стационарная вероятность этого состояния разлагается в произведение безусловных распределений:

.

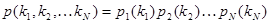Которые представляют собой стационарные вероятности для классической системы M/M/m. Этот удивительный результат называют теоремой Джексона.

Исследование сети с помощью изложенной здесь методики приводит к громоздким системам уравнений для определения интенсивностей входных потоков. Исследованиями было показано, что для получения многих результатов можно, вместо условий глобального равновесия для сети в целом применять условия локального равновесия для отдельных подсистем, что позволяет сильно упростить задачу.

Определим систему уравнений локального равновесия как систему, в которой приравнивается интенсивность потока из данного состояния сети за счет ухода заявок из узла i к интенсивности потока в данное состояние сети за счет поступления требований в узел i .

Покажем это на примере:

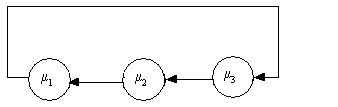
Рис. 1.29 Замкнутая сеть с тремя узлами.

Пусть в замкнутой сети с тремя (N=3) узлами циркулирует ровно два требования (K=2).

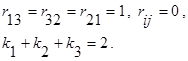
Состояние сети описывается тройками: .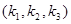

Всего в сети возможно различных состояний .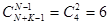

На рис. 1.30 показана диаграмма интенсивностей переходов между этими состояниями.

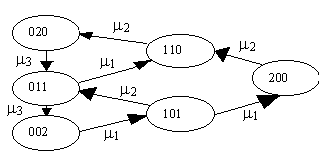
Рис. 1.30 Диаграмма интенсивностей переходов для замкнутой сети с тремя узлами.

Если записать систему уравнений глобального равновесия, то она будет состоять из шести уравнений, одно из которых обычно избыточно из-за существования условия нормировки.

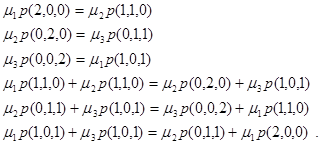
В каждом из этих уравнений левая сторона соответствует потоку исходящему из данного состояния, а правая – потоку, входящему в это состояние.

С точки зрения локального равновесия первые три уравнения именно такими и являются. В остальных уравнениях видно, что первое слагаемое правой части уравновешивается первым слагаемым левой части. И также для вторых слагаемых.

Следовательно, уравнения локального равновесия могут быть выписаны так

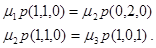
Первое из этих уравнений описывает локальный баланс для узла 1, а второе – для узла 2. Вместе всего образуется девять уравнений локального равновесия, из которых четыре – избыточны. Решение дается следующими формулами

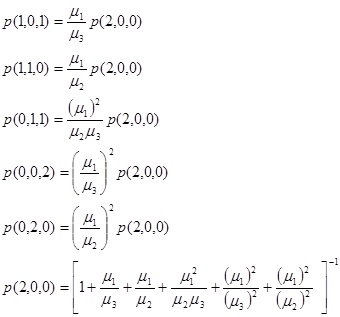
Как видно, решение уравнений локального равновесия отыскать значительно проще. В любом случае поиск стационарных вероятностей сводится к решению больших систем линейных уравнений. Заметим еще раз, что рассмотренные сети массового обслуживания удовлетворяли требованиям эргодической марковской цепи.