Тема 3.2. Численное дифференцирование.

1.Численное дифференцирование.

2.Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона.

3.Погрешность в определении производной.

Дифференциал аргумента равен приращению аргумента 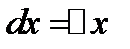. Поэтому дифференциал функции равен произведению от производной на дифференциал аргумента .

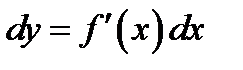Рассмотрим функцию 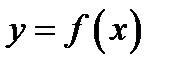. Предположим, что величина 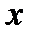получена непосредственным измерением или в результате приближенного вычисления. Тогда при нахождении величины 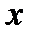мы допускаем не зависящую от нас погрешность 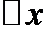. Пусть 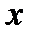– приближенное значение аргумента, 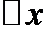-абсолютная погрешность величины 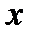, 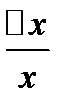- относительная погрешность

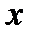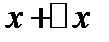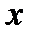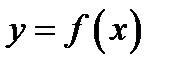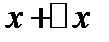величины , -истинное значение измеряемой величины. Тогда определяет приближенное значение , а -ее истинное значение 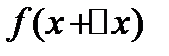, откуда следует, что абсолютная погрешность функции 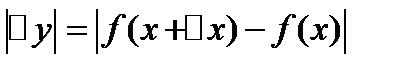. При малых значениях 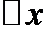величину 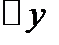можно приближенно заменить дифференциалом : .

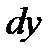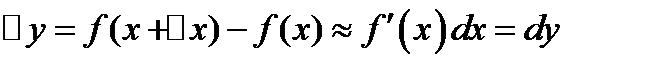Выгода замены приращения функции 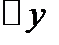ее дифференциалом 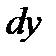состоит в том, что 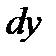зависит от 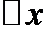линейно, а 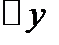представляет собой обычно более сложную зависимость от .

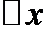Полагая 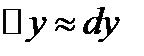, получим выражение для относительной погрешности 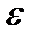величины .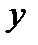

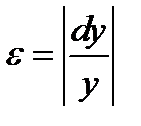Пример: Найти абсолютную и относительную погрешность при замене приращения функции 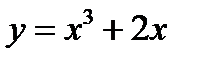ее дифференциалом в точке 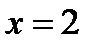при .

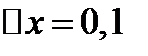Решение.

; ;

;

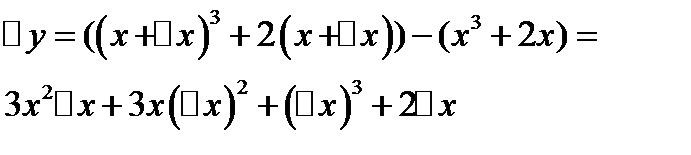
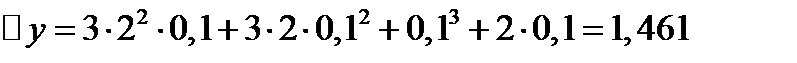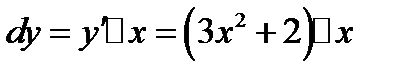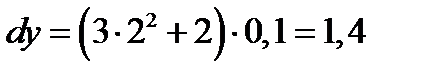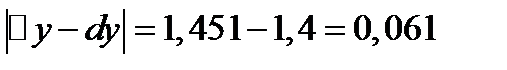
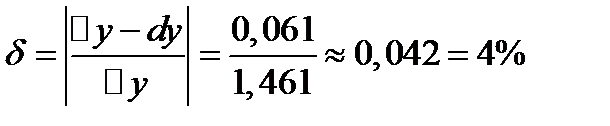
Вопросы для самопроверки:

1.В чем заключается смысл численного дифференцирования.

2.Что называется дифференциалом функции, чему он равен, как обозначается и каков его геометрический смысл?

3.Назовите формулу приближенного дифференцирования, основанные на интерполяционных формулах Ньютона.

4.Какая погрешность называется абсолютной?

5. Какая погрешность называется относительной?

Тема 3.3. Численное решение обыкновенных

Дифференциальных уравнений.

1.Метод Эйлера для решения задачи Коши.

Рассмотрим приближенное решение уравнения (1) на отрезке .удовлетворяющее начальному условию при . Разделим отрезок точками на равных частей (здесь ). Обозначим , следовательно,

Пусть есть некоторое приближенное решение уравнения(1) и

Обозначим

В каждой из точек в уравнении (1) производную заменим отношением конечных разностей: (2) ; ( 2.1)

При будем иметь , или

В этом равенстве известны, следовательно находим

При уравнение (2.1) примет вид или ;

где -известны. Аналогично находим

Т.О. приближенные значения решения в точках найдены. Соединяя на координатной плоскости точки отрезками прямой, получим ломаную - приближенное изображение интегральной кривой. Эта ломаная называется ломаной Эйлера.

Пример: При найти приближенное значение решения уравнения у удовлетворяющего начальному условию при .

Решение

Разделим отрезок на 10 равных частей точками

Следовательно, значения будем искать по формуле (2.1)

или

Таким образом, получаем

В процессе решения составим таблицу

=0	1,000	1,000	0,100
=0,1	1,100	1,200	0,120
=0,2	1.220	1,420	0.142
=0,3	1,362	1,620	0,162
=0,4	1,524	1,924	0,1924
=0,5	1,7164	2,2164	0,2216
=0,6	1.9380	2.5380	0.2538
=0,7	2,1918	2.8918	0,2892
=0.8	2.4810	3.2810	0.3281
=0,9	2,8091	3,7091	0,3709
=1,0	3,1800

Мы нашли приближенное значение

Точное решение данного уравнения, удовлетворяющее укзанным начальным условиям, будет

Следовательно

Вопросы для самопроверки:

1. В чем заключается метод Эйлера для решения задачи Коши?

Тема занятия: Численное решение обыкновенных дифференциальных уравнений (метод Эйлера для решения задачи Коши)

Рассмотрим приближенное решение уравнения (1) на отрезке .удовлетворяющее начальному условию при . Разделим отрезок точками на равных частей (здесь ). Обозначим , следовательно,

Пусть есть некоторое приближенное решение уравнения(1) и

Обозначим

В каждой из точек в уравнении (1) производную заменим отношением конечных разностей: (2) ; ( 2.1)

При будем иметь , или

В этом равенстве известны, следовательно находим

При уравнение (2.1) примет вид или ;

где -известны. Аналогично находим

Т.О. приближенные значения решения в точках найдены. Соединяя на координатной плоскости точки отрезками прямой, получим ломаную - приближенное изображение интегральной кривой. Эта ломаная называется ломаной Эйлера.

Пример: При найти приближенное значение решения уравнения у удовлетворяющего начальному условию при .

Решение

Разделим отрезок на 10 равных частей точками

Следовательно, значения будем искать по формуле (2.1)

или

Таким образом, получаем

В процессе решения составим таблицу

=0	1,000	1,000	0,100
=0,1	1,100	1,200	0,120
=0,2	1.220	1,420	0.142
=0,3	1,362	1,620	0,162
=0,4	1,524	1,924	0,1924
=0,5	1,7164	2,2164	0,2216
=0,6	1.9380	2.5380	0.2538
=0,7	2,1918	2.8918	0,2892
=0.8	2.4810	3.2810	0.3281
=0,9	2,8091	3,7091	0,3709
=1,0	3,1800

Мы нашли приближенное значение

Точное решение данного уравнения, удовлетворяющее укзанным начальным условиям, будет

Следовательно

Контрольная работа

1.Материальная точка массой m кг движется прямолинейно по закону S(t) .

Найти силу, действующую на нее в момент времени t.

Вариант 1 m= 2 кг с;

Вариант 2 m= 3 кг (м) с;

Вариант 3 m= 4 кг с.;

Вариант 4 m= 3 кг (м) с ;

Вариант 5 m= 2 кг (м) с;

Вариант 6 m= 4 кг (м) с;;

Вариант 7 m= 2 кг с;

Вариант 8 m= 2 кг с;

Вариант 9 m= 2 кг с;

Вариант 10 m= 2 кг с;

2. Вариант 1.Напишите уравнение касательной к графику функции в точке .

Вариант 2. Напишите уравнение касательной к графику функции в точке . ;

Вариант 3. Напишите уравнение касательной к графику функции в точке . ;

Вариант 4. Напишите уравнение касательной к графику функции в точке . ;

Вариант 5. Напишите уравнение касательной к графику функции в точке . ;

Вариант 6. Напишите уравнение касательной к графику функции в точке . ; .

Вариант 7. Напишите уравнение касательной к графику функции в точке . ;

Вариант 8. Напишите уравнение касательной к графику функции в точке . ;

Вариант 9. Напишите уравнение касательной к графику функции в точке . ;

Вариант 10. Напишите уравнение касательной к графику функции в точке . ;

3.Исследуйте функцию и постройте ее график:

Вариант 1. Вариант 2. ;

Вариант 3. ; Вариант 4. ;

Вариант 5. ; Вариант 6. ;

Вариант 7. ; Вариант 8. ;

Вариант 9. ; Вариант 10. .

4. Решите задачу:

Вариант 1.

Два тела движутся по прямой из одной и той же точки. Первое тело движется со скоростью м/с, второе – со скоростью м/с. В какой момент и на каком расстоянии от начальной точки произойдет их встреча?

Вариант 2.

Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью м/с, второе – со скоростью м/с. На каком расстоянии друг от друга они окажутся через 10 с?

Вариант 3.

Скорость движения точки м/с. Найдите путь, пройденный за 5 с. от начала движения.

Вариант 4.

Скорость движения точки м/с. Найдите ее путь за 2-ю секунду.

Вариант 5.

Скорость движения точки м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.

Вариант 6.

Скорость движения точки м/с. Найдите: 1)Путь пройденный точкой за 3 с. от начала движения; 2)Путь пройденный точкой за 3-ю секунду.

Вариант 7.

Пружина растягивается на 0,02 м под действием силы 60 Н. Какую работу производит эта сила, растягивая пружину на 0,12?

Вариант 8 .

Под действием силы 80 Н пружина растягивается на 0,02 м. Первоначальная длина пружины равна 0,15 м. Какую работу надо совершить, чтобы растянуть ее до 0,2 м.

Вариант 9 .

Пружина в спокойном состоянии имеет длину 0,1 м. сила в 20 Н растягивает ее на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,12 до 0,14 м?

Вариант 10 .

При сжатии пружины на 0,05 м совершается работа 30 Дж. Какую работу необходимо совершить чтобы сжать пружину на 0.08 м?

5. Найдите общие решения уравнений:

Вариант 1. ; Вариант 2. ;

Вариант 3. ; Вариант 4. ;

Вариант 5. ; Вариант 6. ;

Вариант 7. ; Вариант 8. ;

Вариант 9. ; Вариант 10.

6. Используя признак Даламбера, исследуйте сходимость ряда:

Вариант 1. ; Вариант 2. ;

Вариант 3. ; Вариант 4. ;

Вариант 5. ; Вариант 6. ;

Вариант 7. ; Вариант 8. ;

Вариант 9. ; Вариант10. .

7. Дискретная величина распределяется по закону.

1.Начертить график (т. е. построить многоугольник распределения):

2.Найти математическое ожидание:

3.Найти дисперсию и среднее квадратичное ожидание:

Вариант 1 Х 2 4 7 9 Вариант 2. Х 2 4 5 6

Р 0,1 0,6 0,2 0,1 Р 0,3 0,1 0,2 0,4

Вариант 3. Х 10 15 20 Вариант 4. Х 2 4 6

Р 0,1 0,7 0,2 Р 0,1 0,7 0,2

Вариант 5. Х 2 3 4 9 Вариант 6. Х 12 14 16

Р 0,3 0,1 0,2 0,4 Р 0,2 0,6 0,2

Вариант 7. Х 1 3 5 7 Вариант 8. Х 2 4 6 8

Р 0,3 0,1 0,2 0,4 Р 0,5 0,1 0,3 0,1

Вариант 9. Х 1 3 7 2 Вариант 10. Х 2 4 6

Р 0,3 0,1 0,2 0,4 Р 0,1 0,7 0,2

Методические указания

по изучению дисциплины Математика

для специальности 140414.51 Техническая эксплуатация

и обслуживание электрического

и электромеханического

оборудования (по отраслям)

Уровень подготовки базовый

Тольятти 2012