Практическая работа 6. Матричные игры. Чистые и смешанные стратегии. Решение задач теории игр Графическое решение
Цель: Ознакомить студентов с методикой постановки задач многокритериальной оптимизации и научить методам их решения.
Студенты должны освоить способы преобразования исходной задачи многокритериальной оптимизации к классическим оптимизационным задачам.
Актуальность темы: Методы многокритериальной оптимизации находят широкое применение для рационального планирования крупных разработок.
Теоретическая часть
В реальных ситуациях целесообразность функционирования системы описывается не одним критерием, а несколькими, качество эксплуатации системы оценивается не единственным показателем качества, а совокупностью таких показателей. Такая постановка задачи описания системы с несколькими целями приводит к задаче оптимизации с векторной целевой функцией F(x)=(F1(x), F2(x), ..., Fm(x))
Стратегия взвешенных сумм
Данная стратегия взвешенных сумм преобразует многокритериальную задачу минимизации вектора F(x) в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов
f(x) = ∑ wi Fi(х)2, wi ≥ 0
При этом исходная задача заменяется задачей min f(x).
Далее уже к данной задаче оптимизации уже может быть применен стандартный алгоритм оптимизации без наличия ограничений. В этом случае рассматриваются взвешенные коэффициенты для каждой из выбранных целей.
Метод достижения цели
Описываемый метод представляет собой метод достижения цели Гембики. Данный метод включает в себя выражение для множества намерений разработчика F*(x)=(F1*(x), F2*(x), ..., Fm*(x)), которое связано с множеством целей F(x)=(F1(x),F2(x), ...,Fm(x)). Такая формулировка задачи допускает, что цели могут быть или недо- или передостижимыми, что дает возможность относительно точно выразить исходные намерения при построении оптимального решения. Относительная степень недо- или передостижимости поставленных намерений контролируется посредством вектора взвешенных коэффициентов w = (w1, w2, ..., wm), и может быть представлена как стандартная задача оптимизации с помощью следующей формулировки
min γ
При условии, что
Fi(x) –wi γ ≤ Fi*(x), i =1, 2, ...,m.
Член wi γ вносит в данную задачу элемент ослабления, что, иначе говоря, обозначает жесткость заданного намерения. Весовой вектор w дает исследователю возможность достаточно точно выразить меру взаимосвязи между двумя целями.
Пример.
Пусть фирма производит две модели сборных книжных полок. Их производство ограничено наличием сырья и временем машинной обработки. Для каждого изделия первого типа требуется 3 м2 досок, а для второго – 4 м2. Фирма может получить от своих поставщиков дл 1700 м2 досок в неделю. Для изготовления полок первого типа требуется 12 мин. работы оборудования, для второго типа эта величина составляет 30 мин. В неделю оборудование может эксплуатироваться 160 часов. Сколько изделий каждого типа следует производить фирме в неделю, если одно изделие первого типа приносит 2 ед. прибыли, а второго - 4 ед., известно также, что сборка изделий первого типа требует привлечения трех работников, а второго - 2.
Решение
Для постановки задачи нужно ввести переменные, построить ограничения и целевые функции.
Пусть фирма производит х изделий первого типа и у второго, тогда прибыль составит
P = 2х + 4у → max
среднее число работников на сборке
M = 3x + 2y → min
Целевые функции Р и М отражают два критерия оптимальности в этой задаче.
Введем ограничения:
1) х, у – неотрицательны, по смыслу задачи.
2) ограничение на объем досок
3х+4у ≤ 1700
3)ограничение на время работы оборудования:
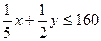, или 2х+5у ≤ 1600.
Таким образом, задача многокритериальной оптимизации примет вид
P = 2х + 4у → max
M = 3x + 2y → min
3х+4у ≤ 1700,
2х+5у ≤ 1600,
х ≥ 0, у ≥ 0.
Найдем допустимое множество, это множество точек на плоскости с координатами, подчиненными ограничениям (четырехугольник ABCD
на рисунке 1.).
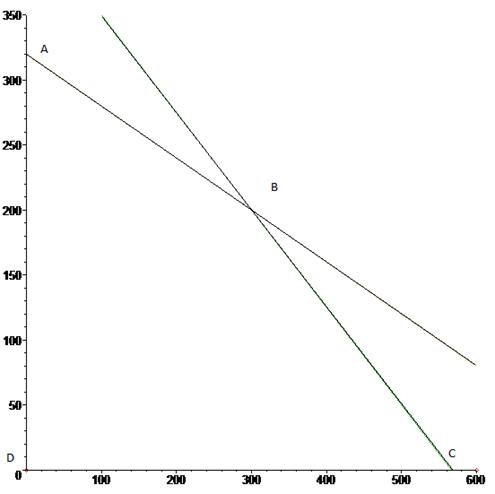
Рис. 1. Допустимое множество решений
Оптимум первой целевой функции Р достигается в точке B с координатами (300;200), второй функции М – в точке D(0; 0).
. Точки D и B являются безусловными точками неулучшаемых решений, поскольку любое улучшение для одной цели P вызывает ухудшение для другой выбранной цели M.
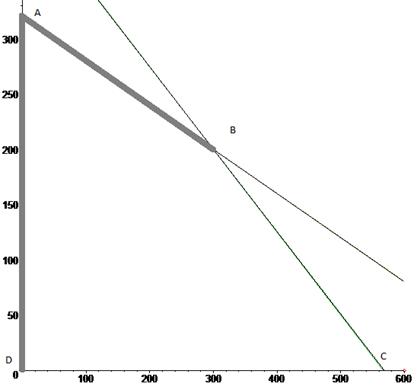
Рис 2.. Множество эффективных решений
Для нашего примера множество неулучшаемых решений - ломаная линия BAD.
Задание к практическому занятию:
Базовый уровень:
В работе необходимо для своего варианта данных, построить математическую модель (целевые функции, ограничения), построить решение (множество неулучшаемых решений).
Исходные условия заданий.
1. Фирма «Лесная пилорама» столкнулась с проблемой наиболее рационального использования ресурсов лесоматериалов, имеющихся в одном из принадлежащих этой фирме лесных массивов. В районе данного массива имеется лесопильный завод и фабрика, на которой изготавливают фанеру. Таким образом, лесоматериалы можно использовать как для производства пиломатериалов, так и для изготовления фанеры.
Чтобы получить 2,5 м3 коммерчески реализуемых комплектов и необходимо израсходовать 2,5 м3 еловых и 7,5 м3 пихтовых лесоматериалов. Для приготовления 100 м2 фанеры требуется 5 м3 еловых и 10 м3 пихтовых лесоматериалов. Лесной массив содержит 80 м3 еловых и 180 м3 пихтовых лесоматериалов.
Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10 м3 пиломатериалов и 1200 м2 фанеры. Доход с 1 м3 пиломатериалов составляет 16 ед., а со 100 м2 фанеры — 60 ед. Известно так же, что производство 1 м2 фанеры наносит экологический ущерб а усл. ед., а 1 м3 пиломатериалов – b усл. ед.
2. Фирме «Иерихонская сталь» предстоит решить, какое количество x1 чистой стали, и какое количество x2 металлолома следует использовать для приготовления (из соответствующего сплава) литья для одного из своих заказчиков. Пусть производственные затраты в расчете на 1 т чистой стали равняются 3 усл. ед., а затраты в расчете на 1 т металлолома — 5 усл. ед. (последнее число больше предыдущего, так как использование металлолома сопряжено с его предварительной очисткой). Заказ предусматривает поставку не менее 5 т литья; при этом заказчик готов купить и большее количество литья, если фирма «Иерихонская сталь» поставит перед ним такие условия.
Предположим, что запасы чистой стали ограничены, и не превышают 4 т, а запасы металлолома не превышают 6 т. Отношение веса металлолома к весу чистой стали в процессе получения сплава не должно превышать 7 : 8. Производственно-технологические условия таковы, что на процессы плавки и литья не может быть отведено более 18 ч; при этом на 1 т стали уходит 3 ч, а на 1 т металлолома - 2 ч производственного времени. Известно так же, что производство 1 т стали из металлолома требует в a раза больше затрат энергии, чем из чистой стали.
3. Фирмой «Супертранзистор» выпускаются радиоприемники трех различных моделей: модель А, модель В и модель С. Каждое изделие указанных моделей приносит доход в размере 8, 15 и 25 соответственно. Необходимо, чтобы фирма выпускала за неделю не менее 100 приемников модели А, 450 приемников модели В и 75 приемников модели С.
Каждая модель характеризуется определенным временем, необходимым для изготовления соответствующих деталей, сборки изделия и его упаковки. Так, в частности, в расчете на 10 приемников модели А требуется 3 ч для изготовления соответствую деталей, 4 ч на сборку и 1 ч на упаковку. Соответствующие показатели в расчете на 10 приемников модели В равны 3.5, 5 и 1.5 ч, а на 10 приемников модели С 5, 8 и 3. В течение ближайшей недели фирма может израсходовать на производство радиодеталей 150 ч, на сборку 200 ч и на упаковку 60 ч.
Cборка модели С предполагает привлечение работников высокой квалификации и обходится на a ед. за 1 час работы дороже.
4. Управляющий фирмы «Свежие нефтепродукты» пытается определить оптимальное распределение имеющейся в его распоряжении сырой нефти (различного сорта) по двум возможным технологическим процессам составления смесей. Технологический процесс 1 характеризуется следующими показателями: из одной единицы объема сырой нефти А и трех единиц объема сырой нефти В получается пять единиц объема бензина X и две единицы объема бензина Y. Технологический процесс 2 характеризуется другими показателями: из четырех единиц объема сырой нефти А и двух единиц объема сырой нефти В получается три единицы бензина X и восемь единиц бензина Y. Объемы продукции, выпускаемой при реализации технологических процессов 1 и 2, обозначим соответственно через x1 и x2. Максимальное количество запасов сырой нефти А равняется 100 единицам объема, а сырой нефти В — 150 единицам объема.
По условиям поставок требуется произвести не менее 200 единиц объема бензина X и 75 единиц объема бензина Y. Доходы с единицы объема продукции, получаемой с помощью технологических процессов 1 и 2 составляют P1 и Р2 соответственно. Угроза срыва поставок сырой нефти 1 сорта составляет a, а для нефти 2 сорта - b.
Повышенный уровень:
5. Авиакомпания «Небесный грузовик» обслуживающая периферийные районы страны, располагает 8 самолетами типа 1, 15 самолетами типа 2, 12 самолетами типа З, которые она может использовать для выполнения рейсов в течение ближайших суток. Грузоподъемность (в тысячах тонн) известна: 45 для самолетов типа 1, 7 для самолетов типа 2, 4 для самолетов типа 3.
Авиакомпания обслуживает города А и В. Городу А требуется тоннаж в 20000 т, а городу В — в 30000 т. Избыточный тоннаж не оплачивается. Каждый самолет в течение дня может выполнить только один рейс.
Расходы, связанные с перелетом самолетов по маршруту центральный аэродром — пункт назначения, указаны в приведенной ниже таблице:
| Тип 1 | Тип 2 | Тип 3 | |
| Город А | 1,4 | ||
| Город В | 3,8 |
Обозначим через хi (i = 1, 2, 3) число самолетов i- го типа, отправленных в город А, а через yi (i = 1, 2, 3) число самолетов ‚ i-го типа, отправленных в город B.
Действуют экологические сборы за доставку грузов в город B, в размере a, b, c ед. за 1 рейс для самолетов 1, 2, 3 типов, соответственно.
6. Авиакомпании «Ночной полет» необходимо решить, какое количество топлива для реактивных самолетов следует закупить у фирм-поставщиков, если число последних равно трем и имеют место следующие требования и ограничения:
1) заправка самолетов производится регулярно в четырех аэропортах.
2) нефтяные компании констатируют следующие возможности поставки топлива в течение ближайшего месяца:
а) 2500000 л - нефтяная компания 1; 2 500 000 л нефтяная компания 1;
б) 5000000 л - нефтяная компания 1; 5 000 000 л нефтяная компания 2;
в) 6000000 л - нефтяная компания 3.
3) авиакомпании требуется следующее количество топлива;
а) 1000000 л в аэропорту 1;
6) 2000000 л в аэропорту 2;
в) 3000000 л в аэропорту 3;
г) 4000000 л в аэропорту 4.
4) стоимости 1 л реактивного топлива с учетом расходов, связанных с доставкой, имеют значения, приведенные в следующей таблице:
| Компания 1 | Компания 2 | Компания 3 | |
| Аэропорт 1 | |||
| Аэропорт 2 | |||
| Аэропорт 3 | |||
| Аэропорт 4 |
Отпускные цены на топливо в аэропортах различаются и составляют a1, a2, a3, a4 ед. соответственно.
7. Фирма «Нитроткань» производит определенного типа мелкие детали для промышленных изделий и продает их через своих посредников-оптовиков по фиксированной поставочной цене 2,50 ед. за штуку. Число посредников-оптовиков равняется пяти. Коммерческие прогнозы указывают на то, что объем месячных поставок составит: посреднику 1 — 3000 штук, посреднику 2 - 3000 штук, посреднику 3 — 10 000 штук, посреднику 4 - 5000 штук, посреднику 5 — 4000 штук.
Фирма располагает следующими производственными мощностями:
завод 1 — 5 000 деталей в месяц,
завод 2 — 10 000 деталей в месяц,
завод 3 — 12 500 деталей в месяц.
Себестоимость одной детали, изготовленной на заводе 1, равняется 1 ед., на заводе 2 —0,90 ед., на заводе 3 — 0,80 ед.
Транспортные расходы (в ед.), связанные с доставкой одной детали в точки оптовой продажи, приведены ниже:
| Клиент 1 | Клиент 2 | Клиент 3 | Клиент 4 | Клиент 5 | |
| Завод 1 | 0.05 | 0.07 | 0.10 | 0.15 | 0.15 |
| Завод 2 | 0.08 | 0.06 | 0.09 | 0.12 | 0.14 |
| Завод 3 | 0.10 | 0.09 | 0.08 | 0.10 | 0.15 |
Стоимость утилизации, отработавших свой срок деталей (за 1 штуку) приводится в таблице:
| Клиент 1 | Клиент 2 | Клиент 3 | Клиент 4 | Клиент 5 | |
| Завод 1 | 0.01 | а | 0.04 | 0.05 | 0.06 |
| Завод 2 | 0.02 | 0.02 | b | 0.02 | 0.04 |
| Завод 3 | 0.02 | 0.02 | 0.05 | c | 0.02 |
Варианты заданий исходных данных к практической работе
| Вариант задания | Исходные данные | Вариант задания | Исходные данные |
| условия 1, a=5, b=2 | условия 4, a=0.06, b=0.05, p1=1, p2=2. | ||
| условия 2, a=1.5 | условия 5, a=1, b=2, c=2. | ||
| условия 3, a=3. | условия 6, a1=1, a2=2, a3=1, a4=2. | ||
| условия 4, a=0.02, b=0.05, p1=3, p2=4.. | условия 7, a=0.01, b=0.02, c=0.03. | ||
| условия 1, a=3, b=2 | условия 1, a=4, b=3 | ||
| условия 2, a=1.2 | условия 2, a=1.8. | ||
| условия 3, a=1. | условия 3, a=1.2. | ||
| условия 4, a=0.03, b=0.05, p1=3, p2=4. | условия 4, a=0.03, b=0.05, p1=5, p2=3. | ||
| условия 1, a=7, b=4 | условия 5, a=2, b=1, c=5. | ||
| условия 2, a=2 | условия 6, a1=3, a2=1, a3=2, a4=1. | ||
| условия 3, a=3. | условия 7, a=0.01, b=0.01, c=0.01. | ||
| условия 4, a=0.06, b=0.03, p1=3, p2=4. | условия 1, a=4, b=1 | ||
| условия 1, a=5, b=5 | условия 2, a=1.6. | ||
| условия 2, a=1.1 | условия 3, a=1.7. | ||
| условия 3, a=1.5. | условия 4, a=0.01, b=0.02, p1=4, p2=4. |
Вопросы для самостоятельной работы
Базовый уровень:
1. Что называется множеством неулучшаемых решений?
2. Перечислите способы преобразования задачи многокритериальной оптимизации к форме классической оптимизационной задачи.
Повышенный уровень:
3. Каким образом строится целевая функция в методе взвешенных сумм?
4. Какая идея положена в основу метода достижения цели?