Практическая работа 3. Симплекс-метод решения задач линейного программирования. Методы нахождения опорного решения.
Цель: Ознакомить студентов c симплекс-методом решения задач линейного программирования. В результате проработки темы студент должен освоить алгоритм метода, уметь его использовать для отыскания оптимальных решений при моделировании..
Актуальность темы: симплекс-метод является основным для решения задач линейного программирования.
Теоретическая часть
Симплекс- метод, позволяющий решить любую задачу линейного программирования, универсален. В настоящее время он используется для компьютерных расчетов, однако несложные примеры с применением симплексного метода можно решать и вручную.
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (или не худшее) значение целевой функции до тех пор, пока не будет найдено оптимальное решение − вершина, где достигается оптимальное значение этой функции, если задача имеет конечный оптимум.
Для реализации симплексного метода − последовательного улучшения решения − необходимо освоить три основныхэлемента:
- способ определения какого-либо первоначального допустимого базисного решения задачи;
- правило перехода к лучшему (точнее, не худшему) решению;
- критерий проверки оптимальности найденного решения.
Для начала использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена с помощью дополнительных выпавнивающих (балансовых) переменных в виде уравнений. Алгоритм конкретной вычислительной реализации этих элементов рассмотрим на примере.
Задача1.
Пусть задана математическая модель в стандартном виде задачи линейного программирования:
12x1 + Зx2 ≤ 264;
4x1 + 5x2 ≤ 136; (1)
Зx1 + 14x2 ≤ 266;
x1 ≥ 0; x2 ≥ 0.
Z = 6x1 + 4x2 → МАХ.
Решение
Решим задачу симплекс-методом. Для этого сначала приведем математическую модель (1) к каноническому виду, когда система ограничений имеет вид уравнений. Это достигается введением в каждое неравенство дополнительных неотрицательных переменных:
x3 ≥ 0; x4 ≥ 0; x5 ≥ 0. Их экономический смысл – неиспользованное сырье каждого вида.
Получим:
12x1 + 3x2 + x3 = 264;
4x2 + 5x2 +x4 = 136; (2)
3x1 + 14x2 + x5 = 266;
x1 ≥ 0; x2 ≥ 0; x3 ≥ 0; x4 ≥ 0; x5 ≥ 0;
U = 6x1 + 4x2 - > МАХ.
Решим систему уравнений математической модели (2), выразив базисные переменные x3 , x4, x5 через свободные x1 и x2.
x 3 = 264 – 12x1 – 3x2;
x4 = 136 – 4x2 – 5x2 ; (3)
x5 = 266 – 3x1 – 14x2;
xj ≥ 0; ( j = 1; 2; 3; 4; 5.); U = 6x1 + 4x2 → МАХ.
Система уравнений математической модели (3) записана в виде, когда часть переменных x3 , x4, x5 выражены через оставшиеся переменные x1 и x2, является общим решением СЛАУ ограничений (ее размер 3×5). Переменные x3 , x4, x5 – базисные (искусственный базис), переменные x1 и x2 – свободные. Придавая свободным переменным произвольные значения и вычисляя базисные переменные по формулам модели (3), можем найти бесконечное множество допустимых (т. е. неотрицательных планов). Заметим, что в общем решении системы уравнений базисными переменными могут быть для данной задачи любые три переменные из пяти (x1 ; x2 ; x3 ; x4; x5), а свободными – оставшиеся две переменные.
Если свободные переменные положить равными нулю и вычислить базисные, то получим допустимый базисный план, который называется опорным: x1 = 0; x2 = 0 ; x3 = 267; x4 = 136; x5 = 266. Базисные переменные равны при этом свободным членам, которые должны быть, следовательно, неотрицательными.
Опорный план – это базисный допустимый план, т. е. неотрицательный план, для которого равны нулю свободные переменные. Количество опорных планов конечно и не превосходит количества базисных решений. Оно равно числу сочетаний из 5 по 3 (или по 2):
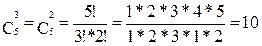 , т. е. опорных планов не больше 10.
, т. е. опорных планов не больше 10.
Основная теорема симплекс-метода говорит о том, что если оптимальный план ЗЛП существует, то его можно найти среди опорных. Это позволяет искать оптимальный план не среди всех допустимых планов, количество которых бесконечно, а лишь среди опорных, число которых конечно и в принципе их можно перебрать, и сравнив по значению критерия оптимальности, выбрать наилучший.
Сущность симплекс-метода состоит в целенаправленном переборе опорных планов для нахождения оптимального. При этом не требуется находить все опорные планы, а достаточно найти один из них и затем переходить к следующему, но так, чтобы решение улучшалось, т. е. значение U увеличивалось, и так до нахождения плана, при котором U – максимально.
Решение ЗЛП симплекс-методом осуществляется с помощью симплекс-таблиц. Математическую модель (3) запишем в виде симплекс-таблицы 1. Базисные переменные помещаем в левый столбец, свободные – в верхнюю строку со знаком «минус», цифрой 1 отмечаем столбец свободных членов
Таблица 1
| Б.п. | -x1 | -x2 | |
 x3 = x4 = x5 = x3 = x4 = x5 = | |||
| U = | -6 | -4 |
Заметим, что в таблице 1 и во всех последующих симплекс-таблицах столбец свободных членов не должен содержать отрицательных элементов в силу условия неотрицательности, за исключением, может быть, элемента U-строки.
Каждая строка таблицы 1 соответствует уравнению модели (3). Каждое уравнение модели (3) может быть получено из таблицы 1 умножением элементов соответствующей строки на элементы верхней строки-заголовка:
x3 = 264*1 + 12*( - x1 ) + 3*( -x2 );
x4 = 136*1 + 4* ( -x1 ) + 5* ( -x2);
x5 = 266*1 + 3* ( -x1 ) + 14*( -x2 );
U = 0*1 - 6*( -x1 ) - 4*( -x2 ).
Полученная таблица 1 называется первой симплекс-таблицей. Она соответствует первому опорному плану:
(x1: x2; x3; x4; x5 ) = ( 0; 0; 264; 136; 266 ).
При таком плане прибыль U = 6*x1 + 4*x2 = 6*0 + 4*0 = 0.
Этот опорный план не является оптимальным, на что указывает наличие отрицательных элементов в U-строке таблицы 1
Перейдем к следующему опорному плану, для этого сначала в таблице 1 выберем ключевой элемент по следующему правилу.
1. Выбираем ключевой (разрешающий) столбец, он соответствует отрицательному элементу U-строки (любому), отметим его стрелкой внизу таблицы 1 Чаще из нескольких отрицательных элементов U-строки выбирают тот, который больше по абсолютной величине. У нас это элемент
« -6 » в U-строке. Выбор ключевого столбца гарантирует увеличение (не уменьшение) значения U.
2. Выбираем ключевую строку, она соответствует минимальному из отношений свободных членов к соответствующим положительным элементам ключевого столбца:
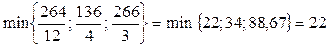 ,
,
что указывает на первую строку, отметим ее стрелкой справа.
Выбор ключевой строки гарантирует сохранение условия неотрицательных переменных.
3. На пересечении ключевой строки и ключевого столбца отмечаем ключевой элемент. Он равен 12.
Строим новую симплекс-таблицу 2, совершая однократное замещение базисной переменной на свободную.
Таблица 2
| Б.п. | -x3 | -x2 | |
 x1 = x4 = x5 = x1 = x4 = x5 = | 1/12 -1/3 -1/4 | ¼ 53/4 | |
| U = | 1/2 | -5/2 |

1. Поменяем местами базисную и свободную переменные, стоящие в ключевой строке и в ключевом столбце: x3 и x1.
2. Ключевой элемент 12 заменим числом, ему обратным: 1/12.
3. Остальные элементы строки разделим на ключевой элемент:
264 : 12 = 22; 3 : 12 = 1/4.
4. Остальные элементы ключевого столбца разделим на ключевой элемент и поменяем знаки на противоположные:
-4 : 12 = -1/3; -3 : 12 = -1/4; 3 : 12 = 1/2.
5. Элементы, не принадлежащие ключевой строке и ключевому столбцу, вычислим по правилу прямоугольника.
Например, вычислим элемент таблицы 2, соответствующий элементу 266 таблицы 1. Для его нахождения в таблице 1 мысленно строим прямоугольник, у которого на концах одной диагонали стоят число 266 и ключевой элемент 12, а на концах другой – числа 264 и 3. Диагональ, содержащая ключевой элемент, считается главной, а другая – побочной. Из произведения элементов по главной диагонали вычитается произведение элементов побочной диагонали и эта разность делится на ключевой элемент:
(266*12 – 264*3):12 = 200.
Полученное число 200 вписываем в таблицу 4.3 на то место, где стояло число 266 в таблице 1.
| 5.п. | -x1 | -x2 | |
      x3 = x4 = x5 = x3 = x4 = x5 = | |||
| U = | -6 | -4 |
Подсчитаем, какое число будет стоять в таблице 2 вместо числа «-4» в U-строке таблицы 1. На рисунке показан прямоугольник, который мы должны мысленно выделить в таблице 1. Главная диагональ прямоугольника содержит рассматриваемый элемент «- 4» и ключевой элемент 12, а побочная диагональ – элементы 3 и «- 6». В результате вычислений получим число, которое вписываем в U-строку таблицы 2:
[ - 4*12 – 3*(-6)] : 12 = ( -48 + 18): 12 = -30:12 = -5/2.
| Б.п. | -x1 | -x2 | |
     x3 = x4 = x5 = x3 = x4 = x5 = | |||
| U = |  -6 -6 | -4 |
Аналогично заполняем все оставшиеся клетки таблицы 2. На месте числа 136 из таблицы 1 в таблице 2 будет стоять число:
( 136*12 – 264*4 ) : 12 = 48.
На месте элемента «0» в U-строке таблицы 1 в таблице 2 запишем число:
[ 0*12 – 264*(-6)] : 12 = 132.
В последнем столбце таблицы 2 на месте элемента «5» будет стоять число:
( 5*12 - 4*3) : 12 = 4.
На месте элемента «14» вписываем в таблице 2 число:
( 14*12 – 3*3) : 12 = 150/12 = 53/4.
Чтобы получить опорный план из симплекс-таблицы 2, полагаем равными нулю свободные переменные x3 и x2, стоящие в верхней строке. Тогда значения базисных переменных x1, x4 и x5 равны значениям, стоящим в первом столбце таблицы 2.
В результате выпишем второй опорный план:
( x1; x2; x3; x4; x5 ) = ( 22; 0; 0; 48; 200),
при котором U = 132. Этот план не является оптимальным, т. к. в U-строке таблицы 2 имеется отрицательный элемент.
Переходим к новой, третьей симплекс-таблице. Для этого сначала в таблице 2 выберем ключевой элемент, повторив предыдущие рассуждения.
1. Отмечаем ключевой столбец. Он содержит отрицательный элемент U-строки: «-5/2».
2. Отмечаем ключевую строку, которая соответствует минимальному из положительных отношений свободных членов к элементам ключевого столбца:
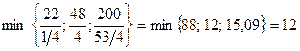 ,
,
что указывает на вторую строку.
3. На пересечении ключевой строки и ключевого столбца в таблице 2 отмечаем ключевой элемент «4».
Переходим к заполнению симплекс-таблицы 3 по правилам 1 – 5.
Таблица 3
| Б.п. | -x3 | -x4 | |
| x1 = x2 = x5 = | 5/48 -1/12 41/48 | -1/16 1/4 -53/16 | |
| U = | 7/24 | 5/8 |
Этой таблице соответствует опорное решение:
(x1; x2; x3; x4; x5 ) = ( 19; 12; 0; 0; 41 ).
Оно является оптимальным, т. к. все коэффициенты U-строки в таблице 3 неотрицательны. Максимальное значение целевой функции U max = 162.
Оно достигается при x1 = 19; x2 = 12. Дополнительные переменные при этом равны: x3 = 0; x4 = 0; x5 = 41. Это означает, что сырье первого и второго видов используется полностью, а сырье третьего вида остается не использованным в количестве 41 кг.
Замечание. При решении задач симплекс-методом количество симплекс-таблиц может быть различным. В рассмотренном решении оно равно трем.
Ответ. Чтобы получить максимальную прибыль в размере 162 тыс. руб., нужно изготовить 19 изделий А и 12 изделий В.
Задание к практическому занятию:
Задачи выбираются в соотвествии со своим вариантом.
Базовый уровень:
Задание 1. Решить симплексным методом задачи (табл. 1).
Таблица 1. Варианты заданий
| Вариант | Задача | Вариант | Задача |
Z(X)=x1+4x2+x3®max, 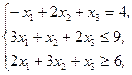 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=-2x1-2x2-2x3®min, 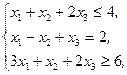 xj³0, j=1,2,3 xj³0, j=1,2,3 |
Продолжение таблицы 1.
Z(X)=2x1+x2-x3®min, 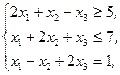 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=-3x1-2x2-2x3®min, 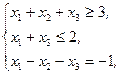 xj³0, j=1,2,3 xj³0, j=1,2,3 | ||
Z(X)=x1-x2+x3®max, 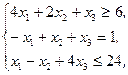 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=-2x1+8x2+3x3®min, 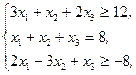 xj³0, j=1,2,3 xj³0, j=1,2,3 | ||
Z(X)=5x1+2x2+x3®max, 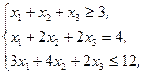 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=6x1+7x2+9x3®min, 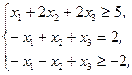 xj³0, j=1,2,3 xj³0, j=1,2,3 | ||
Z(X)=x1-8x2-3x3®max, 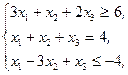 xj³0, j=1,2,3 xj³0, j=1,2,3 | Z(X)=5x1+2x2+x3®max, 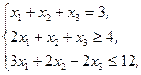 xj³0, j=1,2,3 xj³0, j=1,2,3 |
Повышенный уровень:
Задание 2. Решить методом искусственного базиса задачи линейного программирования (табл. 2)
Таблица 2. Варианты заданий
| Вариант | Задача | Вариант | Задача |
Z(X)=2x1+8x2+3x3+4x4®min, 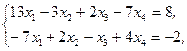 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=2x1+6x2+x3+x4®max, 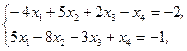 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | ||
Z(X)=2x1+3x2-x3+4x4®min, 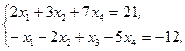 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=2x1+5x2+x3+x4®max, 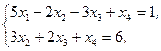 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | ||
Z(X)=4x1+13x2+3x3+6x4®min, 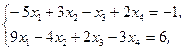 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=9x1+2x2+4x3-8x4®max, 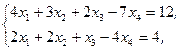 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | ||
Z(X)=x1+x2+3x3+4x4®min, 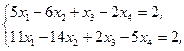 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=x1-2x2-x3+3x4®max, 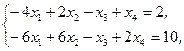 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 |
Продолжение таблицы 2
Z(X)=11x2+x3+4x4®min, 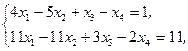 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=2x1+x2-x3-2x4®min, 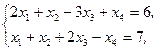 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 |
Вопросы для самостоятельной работы
Базовый уровень:
1. В чем заключается симплекс-метод задачи линейного программирования ?
2. В какой форме необходимо сделать постановку задачи, если применять для ее решения симплекс – метод?
3. Как получить опорное решение задачи линейного программирования для дальнейшего ее решения симплекс-методом?
4. В чем геометрический смысл симплекс-метода?
5. Как строится опорное решение ЗЛП методом искусственного базиса?
Повышенный уровень:
6. Сформулируйте последовательность этапов практической реализации симплекс-метода.
7. Как заполняется исходная симплекс – таблица для решения задачи линейного программирования?
8. Как найти ключевой элемент в исходной симплекс – таблице?
9. Каков алгоритм перехода от одного базиса к другому в поисках оптимального решения задачи?
10. Каков признак оптимального решения в заключительной симплекс – таблице?
