Графический метод решения задач линейного программирования
Примеры выполнения заданий
Задача 3.
Решить геометрически задачу линейного программирования:
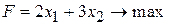
при ограничениях:
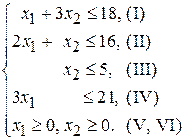
Решение.
Изобразим многоугольник решений на рис. 2. Очевидно, что при 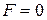 линия уровня
линия уровня 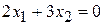 проходит через начало координат (строить ее не обязательно). Зададим, например,
проходит через начало координат (строить ее не обязательно). Зададим, например, 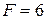 и построим линию уровня
и построим линию уровня 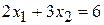 . Ее расположение указывает на направление возрастания линейной функции (вектор
. Ее расположение указывает на направление возрастания линейной функции (вектор 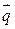 ). Так как рассматриваемая задача — на отыскание максимума, то оптимальное решение − в угловой точке
). Так как рассматриваемая задача — на отыскание максимума, то оптимальное решение − в угловой точке 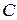 , находящейся на пересечении прямых I и II, т.е. координаты точки
, находящейся на пересечении прямых I и II, т.е. координаты точки 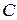
определяются решением системы уравнений
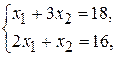 откуда
откуда 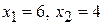 , т.е.
, т.е. 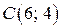 .
.
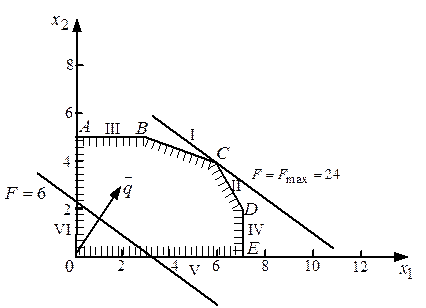
Рис. 2.
Максимум (максимальное значение) линейной функции равен 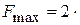
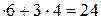 .
.
Итак, 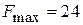 при оптимальном решении
при оптимальном решении 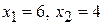 , т.е. максимальная прибыль в 24 руб. может быть достигнута при производстве 6 единиц продукции
, т.е. максимальная прибыль в 24 руб. может быть достигнута при производстве 6 единиц продукции 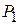 и 4 единиц продукции
и 4 единиц продукции 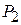 .
.
Замечание. Многоугольник допустимых планов может быть в частности треугольником, четырехугольником и т. д. Может оказаться, что полуплоскости не имеют общих точек. Это означает, что система ограничений противоречива и ЗЛП решений не имеет, т.к. нет допустимых планов.
Задание к практическому занятию:
Базовый уровень:
В заданиях 1− 3 составить экономико-математические модели.
Задание 1. Для производства двух видов изделий 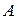 и
и 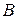 предприятие использует три вида сырья. Другие условия задачи приведены в таблице.
предприятие использует три вида сырья. Другие условия задачи приведены в таблице.
| Вид сырья | Нормы расхода сырья на одно изделие, кг | Общее количество сырья, кг | |
 |  | ||
| I | |||
| II | |||
| III | |||
| Прибыль от реализации одного изделия, ден.ед. |
Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделий 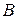 надо выпустить не менее, чем изделий
надо выпустить не менее, чем изделий 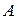 .
.
Задание 2.Рацион для питания животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 70 ден.ед. и содержит: 0,5 ед. жиров, 4 ед. белков, 1 ед. углеводов, 1 ед. нитратов. Один килограмм корма II стоит 16 ден.ед. и содержит 3 ед. жиров, 6 ед. белков, 4 ед. углеводов, 3 ед. нитратов.
Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 9 ед., белков не менее 5 ед., углеводов не менее 4 ед., нитратов не более 11 ед.
Задание 3.На двух автоматических линиях выпускают аппараты трех типов. Другие условия задачи приведены в таблице.
| Тип аппарата | Производительность работы линий, шт. в сутки | Затраты на работу линий, ден.ед. в сутки | План, шт. | ||
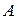 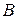 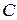 |
Составить такой план загрузки станков, чтобы затраты были минимальными, а задание выполнено не более чем за 10 суток.
Повышенный уровень:
Задание 4.
Найти опорное решение задачи линейного программирования вида 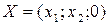 и соответствующее допустимое значение целевой функции
и соответствующее допустимое значение целевой функции  :
:
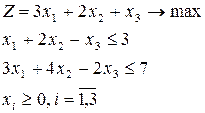
Ответ: 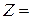 4
4
Задание 5.
Найти опорное решение задачи линейного программирования вида
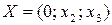 и соответствующие допустимые значения целевой функции
и соответствующие допустимые значения целевой функции  :
:
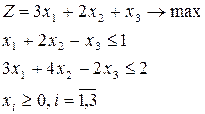
Ответ:  2
2
Задание 6.
Найти опорное решение задачи линейного программирования вида 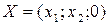 и соответствующее допустимое значение целевой функции
и соответствующее допустимое значение целевой функции  :
:
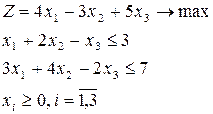
Ответ: 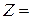 3
3
Задание 7.
Решить графическим методом задачи с двумя переменными (табл. 1)
Таблица 1. Варианты задания 7
| Вариант | Задача | Вариант | Задача |
Z(X)=2x1+4x2®max, 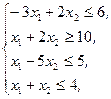 x1³0, x2³0 x1³0, x2³0 | Z(X)=-3x1-x2®min, 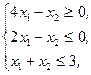 x1³0, x2³0 x1³0, x2³0 | ||
Z(X)=15x1+10x2®max, 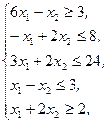 x1³0, x2³0 x1³0, x2³0 | Z(X)=2x1+3x2®max, 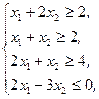 x1³0 x1³0 | ||
Z(X)=3x1+2x2®max, 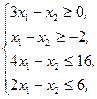 x1³0, x2³0 x1³0, x2³0 | Z(X)=4x1+6x2®max, 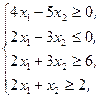 |
Продолжение таблицы 1. Варианты задания 7
Z(X)=2x1+5x2®min, 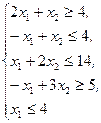 x1³0, x2³0 x1³0, x2³0 | Z(X)=-x1+4x2®min, 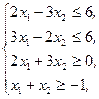 x2³0 x2³0 | ||
Z(X)=2x1-x2®max, 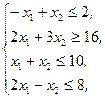 x1³0, x2³0 x1³0, x2³0 | Z(X)=x1+4x2®min, 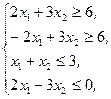 x1³0, x2³0 x1³0, x2³0 |
Задание 8. Решить графическим методом задачи с  переменными (табл. 2).
переменными (табл. 2).
Таблица 2. Варианты задания 8
| Вариант | Задача | Вариант | Задача |
Z(X)=2x1+8x2+3x3+4x4® min, 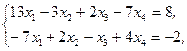 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=2x1+6x2+x3+x4®max, 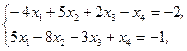 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | ||
Z(X)=2x1+3x2-x3+4x4®min, 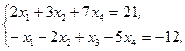 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=2x1+5x2+x3+x4®max, 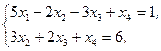 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | ||
Z(X)=4x1+13x2+3x3+6x4®min, 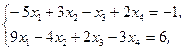 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=9x1+2x2+4x3-8x4®max, 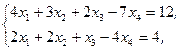 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | ||
Z(X)=x1+x2+3x3+4x4®min, 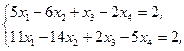 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=x1-2x2-x3+3x4®max, 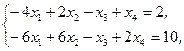 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | ||
Z(X)=11x2+x3+4x4®min, 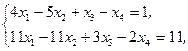 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 | Z(X)=2x1+x2-x3-2x4®min, 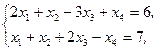 xj³0, j=1,2,3,4 xj³0, j=1,2,3,4 |
Вопросы для самостоятельной работы
Базовый уровень:
1. Что называется экономико-математической моделью?
2. Перечислить основные этапы экономико-математического моделирования.
3. Что называется целевой функцией?
4. Сформулируйте общую постановку задачи линейного программирования.
Повышенный уровень:
5. В чем суть принципа оптимальности в планировании и управлении?
6. В чем заключается геометрическая интерпретация задачи линейного программирования?
7. Каковы основные этапы метода графического решения задачи линейного программирования?
8. Каким может быть множество допустимых решений задачи линейного программирования?
9. Какое направление для целевой функции указывает ее градиент?
10. Когда применяется графический метод ЗЛП?
