Импульсные характеристики идеальных ЦФ различного типа

Аналитические описания импульсных характеристик ЦФ различного типа получаются в общем случае путем выполнения обратного преобразования Фурье их идеализированных частотных характеристик ЧХ H_id(jω).

Для идеального цифрового ФНЧ импульсная характеристика определяется выражением:

; ,

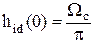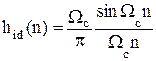n = ±1, ±2, ...

Импульсные характеристики ЦФ типов ФВЧ, ППФ, ПЗФ и МПФ могут быть выражены также через импульсную характеристику цифрового ФНЧ и так называемого всепропускающего фильтра (ВПФ). Для такого идеального фильтра сигнал на выходе совпадает с сигналом на входе:

y(n) = x(n), h_id(0) = 1, h_id(n) = 0 при n ≠ 0;

H_id(jω) = 1 при ‌‌ ‌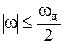

Частотные характеристики ФВЧ, ППФ и ПЗФ могут быть выражены через частотные характеристики ФНЧ и ВПФ [2]. Такая же связь справедлива и для импульсных характеристик, что позволяет непосредственно записать соответствующие им аналитические выражения:

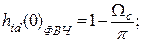
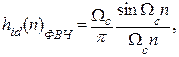
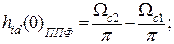
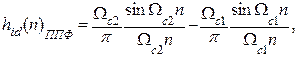
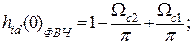
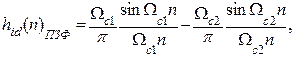
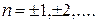
Аналогичным образом находятся соотношения и для конкретного МПФ.

9.4.4 Методика синтеза НФ методом весовых функций и пример синтеза полосового цифрового фильтра

Подводя итог выше сказанному, приведем общую методику синтеза НФ.

По заданному значению затухания частотной характеристики в полосе задерживания а_з с помощью таблицы 9.3 выбирается тип весовой функции, отвечающей условию 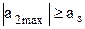, при минимальном значении ширины ее главного лепестка, т.е параметра D. При использовании весовой функции Кайзера по таблице 9.4 находятся соответствующие заданному затуханию а_з параметры данной весовой функции β и D. При этом нужно учитывать, что расчетное значение затухания зависит от вида АЧХ синтезируемого фильтра, его граничных частот и длины весовой функции N и может оказаться как больше, так и меньше оценочного значения а_2max. Чем сложнее АЧХ фильтра (ППФ, ПЗФ, МПФ), тем меньше затухание для одной и той же весовой функции. Это же относится и к неравномерности АЧХ в полосе пропускания.

Для выбранной весовой функции и заданной переходной полосы частотной характеристики фильтра 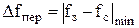в соответствии с приближенным соотношением 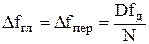находится необходимая длина весовой функции и определяемая ею длина импульсной характеристики фильтра: 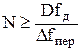, где D – коэффициент зависящий от типа весовой функции.

Значение N приравнивается ближайшему целому нечетному числу.

С помощью обратного преобразования Фурье:

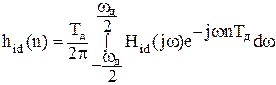
или приведенных выше аналитических выражений вычисляется смещенная вправо импульсная характеристика 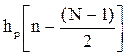, n = 0, . . ., N – 1, соответствующая заданной частотной характеристике H_p(jω).

При этом в качестве частот среза заданной частотной характеристики используют их расчетные значения f_ср, смещенные в полосу задерживания примерно на половину переходной полосы фильтра Δf_пер. Это связано со свойственным данному методу размыванием границ перехода от полосы пропускания фильтра к полосе задерживания (рис. 9.31).

Например, для ППФ:

;

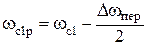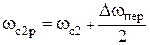
Находится импульсная характеристика фильтра путем весового усечения смещенной вправо на 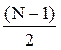отсчетов импульсной характеристики h_p(n):

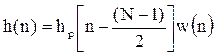, n = 0, . . ., N – 1

Рассчитывается АЧХ фильтра 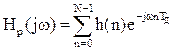и проверяется ее соответствие исходным данным по неравномерности частотной характеристики в полосе пропускания а_п и затуханию в полосе задерживания а_з.

Так как данный метод не обеспечивает точного соответствия исходных и расчетных данных (является итерационным), при необходимости корректируются значения расчетных частот среза ω_с1р, ω_с2р , длины фильтра N и расчеты повторяются.

Выбирается способ реализации НФ (на основе ДВС, ДПФ или частотной выборки) и решаются соответствующие ему задачи реализации.

Следует отметить, что метод весовых функций обеспечивает строгую линейность ФЧХ и постоянство группового времени запаздывания фильтра ввиду четной или нечетной симметрии получаемой этим методом импульсной характеристики h(n).

Далее приводится листинг программы, написанной в среде MathCAD, по синтезу НФ методом весовых функций.