Синтез нерекурсивных фильтров методом весовых функций

Нерекурсивные фильтры относятся к ЦФ с конечной импульсной характеристикой (КИХ – фильтры) и их синтез выполняется по заданной идеализированной частотной характеристике передачи Н_id (jω) = H (iΩ). Синтез заключается в отыскании импульсной характеристики фильтра h(n) конечной длины N, являющейся коэффициентами его передаточной функции .

В данном случае синтез фильтра осуществляется с помощью весовых функций (или с помощью взвешивающих окон), является универсальным методом, что позволяет получить фильтр с любой заданной АЧХ. Он достаточно прост и находит широкое применение на практике. Основной недостаток этого метода в том, что он дает не очень точный результат, что требует проведения итераций в процессе расчета, а также синтезируется фильтр несколько большей длины, чем при других методах.

Частотная характеристика и импульсная связаны парой преобразований Фурье. Поэтому с помощью обратного преобразования Фурье может быть найдена импульсная характеристика h_id(n), которая соответствует заданной идеализированной частотной характеристике:

(9.17)

Однако, импульсная характеристика h_id(n) идеального фильтра не отвечает условию физической реализуемости и имеет бесконечную длину. Поэтому не может быть использована в качестве импульсной характеристики НЦФ, [2].

Получить на основе импульсной характеристики физически реализуемый (КИХ (h_p(n))) фильтр с частотной характеристикой, близкой к заданной, можно путем сдвига h_p(n) вправо на отсчетов и усечения ее за пределами n < 0 и n ≥ N . При этом частотная характеристика фильтра аппроксимируется усеченным рядом Фурье с коэффициентами :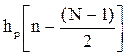

Однако это усечение приводит к колебаниям АЧХ, ухудшающим параметры фильтра. Для улучшения аппроксимации импульсную характеристику НЦФ 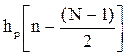домножают на специальную весовую функцию или окно w(n) конечной длины N:

(9.18)

Выбор взвешивающего окна определяется необходимой степенью подавления в полосах непропускания синтезируемого фильтра. Отметим, что простое усечение импульсной характеристики эквивалентно умножению на прямоугольную весовую функцию w_R(n)=1, при n = 0, 1, 2, . . . , N-1.

Полученной таким образом импульсной характеристике соответствует частотная характеристика фильтра , определяемая сверткой в частотной области заданной частотной характеристики H_id(jω) с частотной характеристикой весовой функции w(jω):

,

где * – символ свертки,

– частотная характеристика весовой функции.

Данные преобразования во временной и частотной области иллюстрируются графиками, приведенными на рисунке 9.30.

Частотная характеристика весовой функции на рисунке 9.30 имеет главный лепесток шириной Δω_гл и боковые лепестки, уровень которых характеризуется максимальным по модулю значением а_бmax и площадью под боковыми лепестками. Свертка в частотной области осуществляется графически путем смещения по частоте в пределах зеркально отображенной частотной характеристики весовой функции и вычисления площади перекрытия ее с заданной частотной характеристикой H_id(jω).

Рис. 9.30 Графическая иллюстрация синтеза НФ методом окон

Из рисунка следует, что переходная полоса частотной характеристики фильтра H_р(jω) определяется шириной главного лепестка частотной характеристики весовой функции: Δω_пер ≈ Δω_гл, а пульсации в полосе пропускания и задерживания а_п, а_з связаны с уровнем ее боковых лепестков. Это определяет требования к весовой функции, которая должна иметь:

- минимальную ширину главного лепестка Δω_гл;

- минимальный уровень боковых лепестков а_бmax и минимальную площадь под боковыми лепестками;

- минимальную длину N.

Требования эти достаточно противоречивы. Так, более гладкие весовые функции имеют меньший уровень боковых лепестков, но большую ширину главного лепестка, уменьшающуюся с увеличением длины весовой функции N. Этим объясняется многообразие используемых на практике типов весовых функций. Обычно на практике чаше всего используют окна Хэмминга и Блэкмана.