Глава 9. цифровая фильтрация
В общем случае под фразой цифровая фильтрация нужно понимать любое преобразование над дискретным сигналом, а не только выделение сигнала определенной полосы частот. В этом смысле понятие «цифровой фильтрации» и «дискретная система» - это одно и тоже. Однако, в этом разделе речь пойдет именно о цифровых фильтрах, т.е. устройствах работающих с дискретными сигналами и выделяющих определенный спектр.
Помимо очевидных преимуществ устранения ошибок в фильтре стабильности характеристик, и т.д., цифровые фильтры позволяют получить такие технические характеристики, которые трудно или даже невозможно получить в аналоговых фильтрах. Кроме того, характеристики ЦФ могут быть легко изменены программно. Сами фильтры могут быть реализованы либо в виде программного продукта, либо с использованием специализированных БИС или цифровых сигнальных процессоров.
Процесс проектирования ЦФ состоит их тех же этапов, что и проектирование аналоговых фильтров. Вначале формулируются требования к желаемым характеристикам фильтра, по которым затем рассчитываются параметры фильтра. Амплитудная и фазовая характеристики формируются аналогично аналоговым фильтрам.
В задачу проектирования ЦФ так же входит выбор подходящей структуры реализации дискретного фильтра с учетом точности вычислений. Основное различие между ЦФ и АФ состоит в том, что вместо вычисления сопротивлений, емкостей и индуктивностей в аналоговых системах, рассчитываются значения коэффициентов. Эти коэффициенты {ai}, {bi} являются аналогами физических сопротивлений, емкостей и индуктивностей АФ. Их и необходимо найти в первую очередь при синтезе ЦФ
Дискретная система, как и аналоговая, полностью может быть описана математическим оператором, устанавливающим связь между выходным и входным сигналами или последовательностями [1]:
y(i) = F(x(i)) (9.1)
Оператор системы, реализуется аппаратными или программными средствами, и называется алгоритмом обработки системы.
В случае одномерной цифровой фильтрации последовательность отсчетов x(i) входного сигнала преобразуется в последовательность отсчетов выходного сигнала y(i) по общей формуле:
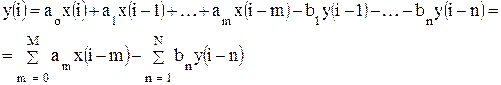 (9.2)
(9.2)
Значения m и n могут быть любыми натуральными числами, а коэффициенты ai, bi могут быть любыми действительными числами (положительными и отрицательными). M ≥ N обозначает порядок уравнения. Устройство или программу, реализующие разностное уравнение (9.2) и называют дискретным или цифровым фильтром.
Сигнал на выходе ЦФ равен сумме текущего отсчета входного сигнала и предыдущих (N и M) отсчетов входного и выходного сигналов взятых с весовыми коэффициентами ai, bi.
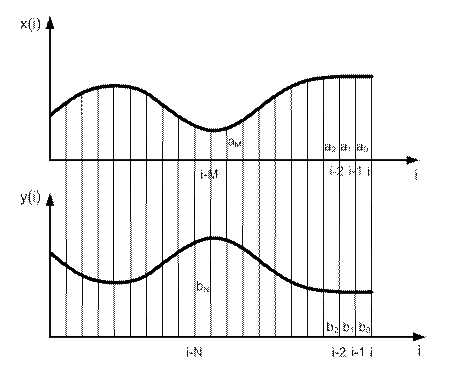
Рис. 9.1 Представление дискретного сигнала
Если хотя бы один из коэффициентов bi не равен нулю, ЦФ называется рекурсивным, [2]. Рекурсия означает наличие в фильтре обратных связей, и текущее значение выходного сигнала будет определяться не только входным сигналом, но и более ранними значениями выходного сигнала y(i – n), (рис. 9.1). Такие фильтры еще называют фильтрами с бесконечной импульсной характеристикой (БИХ – фильтры), так как они «помнят» все предыдущие значения входного и выходного сигналов и их импульсная характеристика бесконечна (рис. 9.2).
РФ позволяют производить обработку сигнала с высокой точностью, так как у них импульсная характеристика не усекается, позволяют организовать алгоритмы обработки сигналов практически любой сложности, простая схемная реализация, т.е. содержат относительно небольшое число элементов. Однако, из-за наличия обратных связей такие фильтры склонны к самовозбуждению, а их фазовая характеристика в общем случае нелинейная.
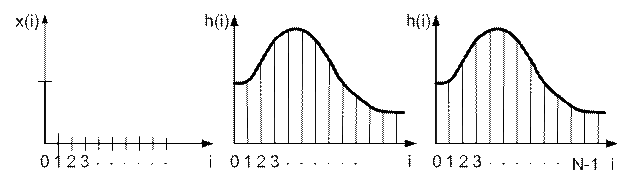 а) б) в)
а) б) в)
Рис. 9.2 Единичный входной импульс (а) и импульсные характеристики: БИХ – фильтра (б) и КИХ – фильтра (в)
Если все коэффициенты bi=0 , то уравнение (9.2) преобразуется к виду:
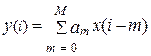 , (9.3)
, (9.3)
тогда ЦФ называется нерекурсивным. Его импульсная характеристика становится конечной и фильтр называется фильтром с конечной импульсной характеристикой (КИХ – фильтр) (рис. 9.2, в).
Дискретная временная свертка для НФ имеет конечные пределы суммирования, определяемые конечной длиной импульсной характеристики фильтра N:
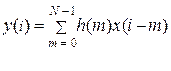 (9.4)
(9.4)
Сравнивая выражения (9.3) и (9.4) видно, что дискретная временная свертка (ДВС) может непосредственно использоваться при реализации алгоритма обработки в НФ, и отсчеты импульсной характеристики являются коэффициентами фильтра.
НФ имеют почти линейную ФЧХ, мощность собственных шумов, как правило, меньше чем у РФ, проще вычисление коэффициентов, всегда устойчивы и просты в настройке. Однако НФ содержат большое число элементов цепи и не позволяют производить обработку дискретных сигналов с высокой точностью.
Устойчивость ЦФ можно оценить по импульсной характеристике. Для устойчивого ЦФ импульсная характеристика затухает со временем, что математически 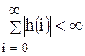 . Обобщенная структурная схема ЦФ имеющего как рекурсивную, так и нерекурсивную части показаны на рис. 9.3.
. Обобщенная структурная схема ЦФ имеющего как рекурсивную, так и нерекурсивную части показаны на рис. 9.3.
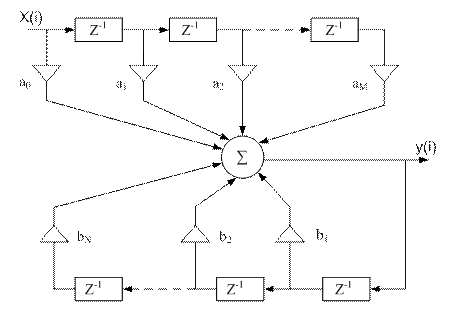
Рис. 9.3 Обобщенная структурная схема ЦФ
Здесь блоки Z-1 выполняют роль линии задержки сигнала на один отсчет (Т = 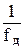 ). Операционные усилители определяют коэффициенты фильтра.
). Операционные усилители определяют коэффициенты фильтра.
