Упрощение вида ответа при символьных расчетах

При решении алгебраических уравнений сложного вида выражения ответа могут получиться просто огромными. Так при попытке решить полином 5-й степени с параметром ответ занимает три листа в длину и полтора в ширину. Естественно, работать с такими выражениями неудобно.

Чтобы упростить вид ответа, достаточно после вектора результата поставить оператор численного вывода « = ». При этом сложные подкоренные и степенные выражения символьного ответа будут пересчитаны в простую десятичную дробь.

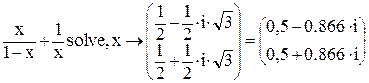
Трудности из-за размера выражений ответа характерны также для уравнений с параметрами и особенно для уравнений с буквенными коэффициентами. Так, вектор решения кубичного уравнения, заданного в общем виде, занимает несколько листов. Естественно, работать с такими выражениями практически невозможно.

Однако можно построить график зависимости величины ответа от значения параметра или коэффициента. Для этого следует проименовать вектор ответа и в дальнейшем работать с его элементами.

Пример

Зависимость величины корня кубического уравнения 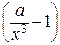от значения коэффициента a.

Запишем: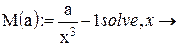

Получим: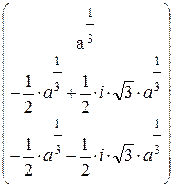

Обозначим: x(a):=M(a)_o и построим график x(a):

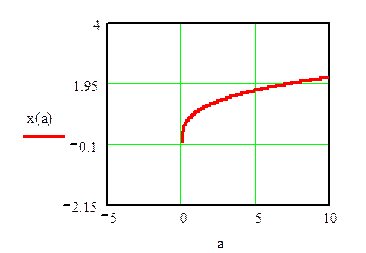
Рис. 6.42 График x(a)

Глядя на график можно заметить следующее:

Действительное решение равно значению параметра в степени 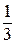, поэтому оно должно принимать и отрицательные значения.

По правилам алгебры:

,

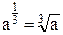а извлечь кубический корень можно из любого действительного числа, и поэтому соответствующая функция должна быть определена на всей числовой оси:

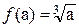
График этой функции представляем на рис. 6.43.

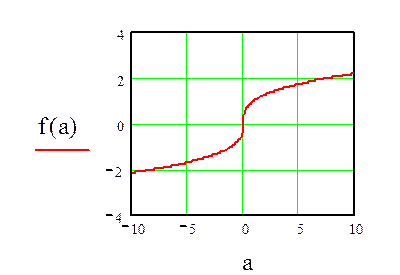
Рис. 6.43 График функции f(a)

Вопрос: почему же кривая x(a) (Рис. 8.3) не существует при отрицательных значениях параметра a?

Все дело в существовании одного очень тонкого отличия в MathCAD между записью кубического корня в виде непосредственного математического оператора и как степени.

Разница эта заключается в том, что оператор рассматривает подкоренное выражение как действительное число, а степень – как комплексное.

При этом, если операция проводится над действительным отрицательным числом, то в первом случае ответ будет также действительным отрицательным числом, а во втором – комплексным выражением.

При возведении и того, и другого ответа в куб будет получено, в рамках рабочей точности, исходное число.

Аналогичная ситуация существует и для корней других нечетных степеней:

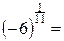(1,12923107663412 + 0,331572160749093i)

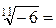-1,17690395624285

(1,12923107663412 +0,331572160749093i)¹¹= -5,99999999999994

(-1,17690395624285)¹¹= -5,99999999999985

Таким образом запись в виде 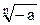при n-нечетном позволяет получить значения корня в виде действительного числа.

Вопросы для самоконтроля

1. Назовите два пути символьных преобразований в среде MathCAD

2. Достоинства и недостатки этих двух методов

3. Состав подменю «ВЫЧИСЛИТЬ» меню «СИМВОЛИЧЕСКИЕ»

4. Назначение подменю «СТИЛЬ ВЫЧИСЛЕНИЙ» меню «СИМВОЛИЧЕСКИЕ»

5. Способы упрощения ответа при символьных расчетах

6. В чем состоит различие записей 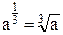при расчетах в среде MathCAD

Оптимизация в расчетах РЭА

Оптимизация есть процедура поиска и нахождения такой комбинации значений параметров устройства определенной структуры, при которой характеристики объекта имеют наилучшие значения согласно выбранному критерию.

Инженерное проектирование устройства, превосходящего по своим параметрам другие устройства данного класса, и есть процесс оптимизации.

Оптимизация в сочетании с перебором определенного числа структур проектируемого объекта перерастает в процедуру синтеза.