Амплитудно-частотная характеристика (АЧХ)

Это зависимость модуля комплексного коэффициента передачи от частоты:

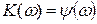
Определение АЧХ с помощью пакета программ MathCAD для электрической цепи 2-ого порядка (рис. 6.32).

Рис.6.32 Электрическая цепь 2-ого порядка

Для коэффициента передачи цепи запишем следующее выражение:

,

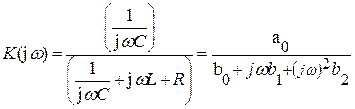где ,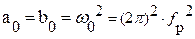

, ,

, .

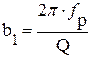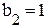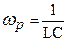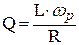Примем в программе следующие обозначения:

fp – резонансная частота (Гц);

tk _– время (сек);

Q – добротность цепи;

K(f) – комплексный коэффициент передачи K(jω);

A(f) – модуль комплексного коэффициента передачи (в градусах) (ФЧХ);

D(f) – действительная часть комплексного коэффициента передачи;

M(f) – мнимая часть комплексного коэффициента передачи;

NT – число точек отсчета по оси времени;

TH – шаг этого отсчета;

Vb – верхний предел интегрирования по частоте;

Vn – нижний предел интегрирования по частоте;

Фk– переходная характеристика Ф(t);

Нk– импульсная характеристика H(t);

Нижний предел интегрирования не берут равным 0, а принимают равным какому-либо малому значению, например, 0,0001, чтобы избежать деления на 0 при определении переходной характеристики.

Программа расчета частотных характеристик цепи

fp:=10 Q:=5

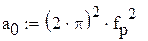
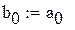
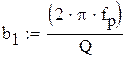
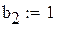
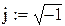
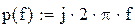
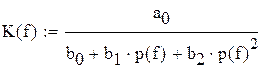
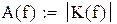
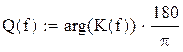
Далее определяются АЧХ и ФЧХ и строятся их графики

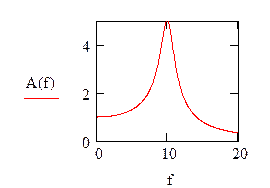
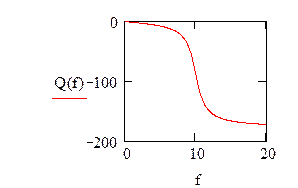
Рис.6.33 График АЧХ Рис.6.34 График ФЧХ

Определение переходной и импульсной характеристик

Переходная характеристика Ф(t)

Это есть зависимость выходного сигнала Y(t) от времени при входном сигнале в виде единичной функции:

l(t)=1 при t≥0

l(t)=0 при t<0

Расчет можно вести по следующим формулам, выраженным через действительную Re(ω) и мнимую Im(ω) части коэффициента передачи K(jω).

,

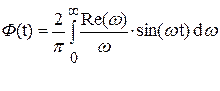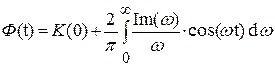
Импульсная характеристика h(t)

Это есть отклик объекта на входное воздействие в виде единичного импульса δ(t):

,

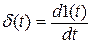спектральная плотность которого:

_,

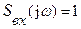и потому:

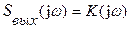
При этом импульсная характеристика согласно обратному преобразованию Фурье:

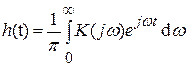
h(t) можно найти также по действительной или мнимой части коэффициента передачи K(jω):

,

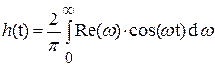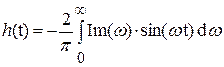
Ниже следует расчет переходной и импульсной характеристики с помощью пакета программ MathCAD для электрической цепи 2-ого порядка (рассмотренной выше).

Все параметры, K(f) и A(f) получены в разделе 5.3.

Далее используются обозначения:

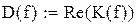– действительная часть коэффициента передачи;

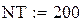– число точек расчета;

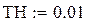– шаг расчета;

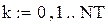– дискретно на один изменяющийся параметр;

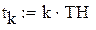– аргумент (дискретное время);

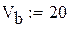– верхний предел интегрирования;

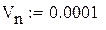– нижний предел интегрирования.

Переходная характеристика запишется в виде:

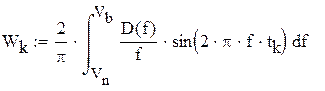
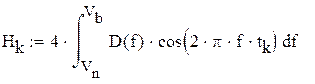
Вопросы для самоконтроля

1.Дать понятие коэффициента передачи линейного устройства

2.Дать понятие амплитудно-частотной характеристики линейного устройства

3.Дать понятие фазо-частотной характеристики линейного устройства

4.Дать понятие переходной характеристики линейного устройства

5.Дать понятие импульсной характеристики линейного устройства

Методы решения в среде «MathCAD» алгебраических и трансцендентных уравнений и организация вычислений по циклу