Оптимальная длина кодовой комбинации при использовании циклического кода в системе с РОС

Длина кодовой комбинации n должна быть выбрана таким образом, чтобы обеспечить наибольшую пропускную способность канала связи. При использовании корректирующего кода кодовая комбинация содержит n разрядов, из которых k разрядов являются информационными, а r разрядов – проверочными:

n= k+r (3.1)

Если в системе связи используются двоичные сигналы (сигналы типа «1» и «0») и каждый единичный элемент несет не более одного бита информации, то между скоростью передачи информации и скоростью модуляции существует соотношение

C = (k/n)*B, (3.2)

где С – скорость передачи информации, бит/с;

В – скорость модуляции, Бод.

Очевидно, что тем меньше r, тем больше отношение k/n приближается к 1, тем меньше отличается С и В, т.е. тем выше пропускная способность системы связи.

Известно также [3, стр. 104], что для циклических кодов с минимальным кодовым расстоянием d₀=3 справедливо соотношение

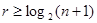(3.3)

Видно, что чем больше n, тем ближе отношение k/n к 1. Так, например, при n = 7, r=3, k=4, k/n = 0,571; при n = 255, r=8, k=247, k/n = 0,964; n = 1023, r=10, k=1013, k/n = 0,990.

Приведенное утверждение справедливо для больших d₀, хотя точных соотношений для связей между r и n нет. Существуют только верхние и нижние оценки, указанные на стр. 104 [3].

Из изложенного можно сделать вывод, что с точки зрения внесения постоянной избыточности в кодовую комбинацию выгодно выбирать длинные кодовые комбинации, так как с увеличением n относительная пропускная способность увеличивается, стремясь к пределу, равному 1.

R= C/B= k/n (3.4)

В реальных каналах связи действуют помехи, приводящие к появлению ошибок в кодовых комбинациях. При обнаружении ошибки декодирующим устройством в системах с РОС производится переспрос группы кодовых комбинаций. Во время переспроса полезная информации уменьшается.

Можно показать, что в этом случае

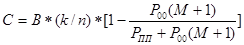, (3.5)

где Р₀₀ – вероятность обнаружения ошибки декодером (вероятность переспроса);

Р_ПП – вероятность правильного приема (безошибочного приема) кодовой комбинации;

М – емкость накопителя передатчика в числе кодовых комбинаций.

При малых вероятностях ошибки в канале связи (Р_ош.< 10^-3) вероятность Р₀₀ также мала, поэтому знаменатель мало отличается от 1 и можно считать

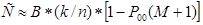(3.6)

При независимых ошибках в канале связи, при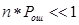

,

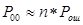тогда

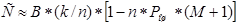(3.7)

Емкость накопителя [2, стр. 323]

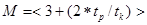, (3.8)

где t_p – время распространения сигнала по каналу связи, с;

t_k – длительность кодовой комбинации из n разрядов, с.

Знак < > - означает, что при расчете М следует брать большее ближайшее целое значение. Но

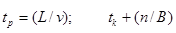, (3.9)

где L – расстояние между оконечными станциями, км;

v – скорость распространения сигнала по каналу связи, км/с;

B – скорость модуляции, Бод.

После простейших подстановок окончательно имеем

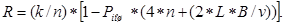(3.10)

Нетрудно заметить, что при Р_ош = 0 формула (3.10) превращается в формулу (3.4).

При наличии ошибок в канале связи величина R является функцией P_ош, n, k, B, L, v. Следовательно, существует оптимальное n (при заданных P_ош, B, L, v), при котором относительная пропускная способность будет максимальной.

Формула (3.10) еще более усложняется в случае зависимых ошибок в канале связи (при пакетировании ошибок).

Выведем эту формулу для модели ошибок Пуртова.

Как показано в [1], число ошибок t_об в комбинации, длинной в n разрядов, определяется формулой 7.38 [1]. Для обнаружения такого числа ошибок находим циклический код с кодовым расстоянием d₀ не менее 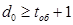. Поэтому, согласно формуле 7.38 [1], необходимо определить вероятность

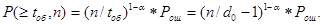
Как показано [4], с некоторым приближением можно связать вероятность 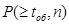с вероятностью не обнаружения декодером ошибки Р_НО и числом проверочных разрядов в кодовой комбинации

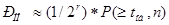(3.11)

Подставляя значение 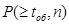в (9) с заменой t_об на d₀-1, имеем

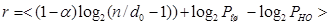(3.12)

При расчетах на микрокалькуляторах удобнее пользоваться десятичными логарифмами.

После преобразований

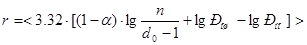(3.13)

Возвращаясь к формулам (3.7) и (3.10) и производя замену k на n-r с учетом значения r, из формулы (3.13) получим

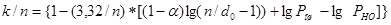
Второй член формулы (3.10) с учетом группирования ошибок по соотношению 7.37 [1] примет вид

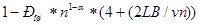
Окончательно

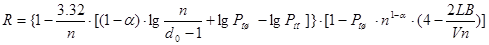(3.14)

Примем n равной 31. Если при расчете пропускная способность R будет меньше 0.6, то рассчитаем ее для n равной 63.

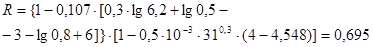
Итак, в моем случае:

n = 31

R = 0.695

Параметры циклического кода

К параметром циклического кода относятся:

n – длина кодовой комбинации (разрядов);

k – длина информационной части кодовой комбинации (разрядов);

r – длина проверочной части кодовой комбинации (разрядов);

g (x) – вид образующего полинома циклического кода.

После определения оптимальной длины кодовой комбинации n, обеспечивающей наибольшую относительную пропускную способность R, по формуле (3.13) определяют число проверочных разрядов:

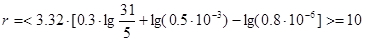
Так как n , в моем случае, равно 31, то воспользовавшись формулой (3.1), определим число информационных символов k:

k = 31 – 10 = 21

Выбираем образующий полином согласно последней цифре зачетной книжки и числу проверочных символов, которые определяют степень g(x):

g (x) = х¹⁰+х⁴+х³+х+1