Двумерные нестационарные ортогональные разложения
И спектральные характеристики
Пусть функция двух независимых переменных х(τ1, τ2) интегрируема в квадрате с весом ρ = (t1, τ1, t2, τ2) = ρ1(t1, τ1)ρ2(t2, τ2) на нестационарном прямоугольнике a1(t1) ≤ τ1 ≤ b1(t1), a2(t2) ≤ τ2 ≤ b2(t2), т.е.

Будем аппроксимировать функцию х(τ1, τ2) на нестационарном прямоугольнике с образующими отрезками [a1(t1), b1(t1)], [a2(t2), b2(t2)] линейной комбинацией n+1 первых по j и i функций нестационарной ортонормированной вещественной системы ~{qj(t1,τ1) pi(t2, τ2)}, где функции qj(t1,τ1) связаны с функцией веса ρ1(t1,τ1), а функции pi(t2, τ2) - с ρ2(t2,τ2), т. е.

В выражении коэффициенты Сji(t1, t2) подлежат выбору(определению). За меру точности приближения обобщенного полинома xn(t1, τ1, t2, τ2) к функции x(τ1, τ2) примем функцию

Можно показать, что минимум функции Jn(t1, t2) для каждых значений независимых переменных t1, t2 достигается, если коэффициенты Сji(t1, t2) являются коэффициентами Фурье, определяемыми формулами

Минимальное значение двойного интеграла описывается формулой

Если системы функций {qj(t1,τ1) pi(t2, τ2)} замкнуты соответственно на отрезках [a1(t1), b1(t1)], [a2(t2), b2(t2)], то и система {qj(t1,τ1) pi(t2,τ2)} замкнута на нестационарном прямоугольнике с образующими отрезками [a1(t1), b1(t1)], [a2(t2), b2(t2)], т.е.

Учитывая выражение (IV.29) для замкнутой системы функций из формулы (IV.28), получим

Функция X(j, i, t1, t2), ординатами которой являются коэффициенты Фурье функции x(τ1, τ2), представляет собой двумерную спектральную характеристику функции x(τ1, τ2) по нестационарному ортонормированному базису {qj(t1,τ1) pi(t2,τ2)}, называемую в дальнейшем просто двумерной нестационарной спектральной характеристикой. Последняя, согласно выражению (IV.27), ищется по формуле

Двумерная нестационарная спектральная характеристика является функцией в общем случае четырех аргументов: двух дискретных j и i и двух непрерывных t1 и t2. Она может быть представлена в виде квадратной матрицы бесконечного порядка, элементами которой являются ее ординаты Сji(t1, t2) (Переменная j указывает номер строки, а i – номер столбца)

Квадратная матрица конечного порядка описывает функцию времени в общем случае лишь приближенно.
Обратный переход от двумерной спектральной характеристики к функции времени осуществляется по формуле

и практически может быть произведен путем численного или графического суммирования конечного числа членов этого ряда вначале по одной переменной, например τ1, а затем по другой – τ2. Понятие двумерных нестационарных спектральных характеристик можно распространить также на дельта - функции и ее производные.
В дальнейшем под знаком спектральных характеристик, когда это необходимо, будем писать символ системы функций, относительно которой определена спектральная характеристика, например  (j, i, t1, t2).
(j, i, t1, t2).
Нестационарные передаточные функции систем
С переменными параметрами
Всякая линейная система с переменными параметрами описывается тремя нестационарными передаточными функциями. При этом все передаточные функции определяются как нестационарные спектральные характеристики импульсной переходной функции системы управления k(θ,τ)относительно ортонормированных систем функций, имеющих весовые функции, равные единице, и заданных на отрезках типа [t - T(t), t] или на квадратах с образующими отрезками этого типа.
Нестационарной нормальной
передаточной функцией N (j, t, τ) линейной системы назовем нестационарную спектральную характеристику ее нормальной импульсной реакции

Нестационарной сопряженной передаточной функцией Н(i, t, θ) линейной системы назовем нестационарную спектральную характеристику ее сопряженной импульсной реакции , она представляется матрицей-строкой):

Двумерной нестационарной передаточной функцией
W(j, i, t, t) линейной системы назовем двумерную нестационарную спектральную характеристику ее импульсной переходной функции:
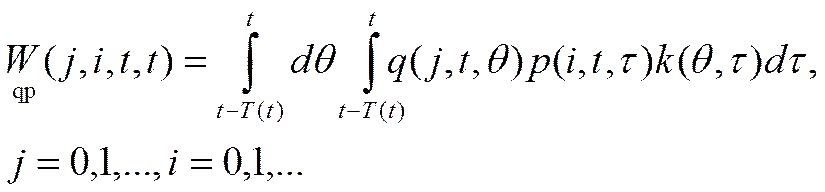
Отметим, что при вычислении передаточных функций по формулам следует иметь в виду, что
 при θ < τ.
при θ < τ.
Обратный переход от нестационарных передаточных функций к импульсной переходной функции осуществляется по формулам



Точность аппроксимации импульсной переходной функции усеченными рядами Фурье определяется соответственно выражениями



Ординаты нестационарных передаточных функций инерционных систем стремятся к нулю при неограниченном росте дискретных аргументов. Поэтому инерционные системы приближенно можно описывать конечным числом ординат передаточных функций. Связь двумерной нестационарной передаточной функции с одномерными устанавливается формулами




Итак, зная одну передаточную функцию, можно найти две остальные..
Например, 
 постоянная величина,
постоянная величина,

 постоянная величина,
постоянная величина,