И спектральные характеристики

Пусть функция времени х(τ) интегрируема в квадрате с ве­сом ρ(t, τ) на нестационарном отрезке [a(t), b(t)], т. е.

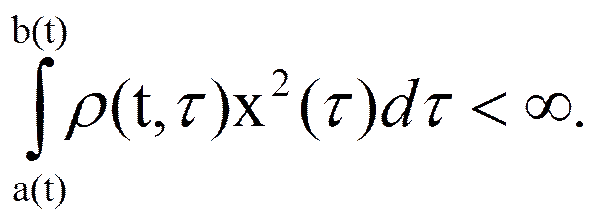
Будем аппроксимировать функцию x(τ) на нестационарном отрезке [a(t), b(t)] линейной комбинацией первых n+1 функций нестационарной ортонормированной вещественной системы {ψ_i(t, τ)}:

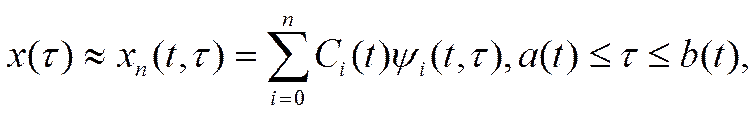
где коэффициенты С_i(t) подлежат выбору.

За меру точности приближения обобщенного полинома х_n(t, τ) к функции x(τ) на нестационарном отрезке [a(t), b(t)] примем функцию

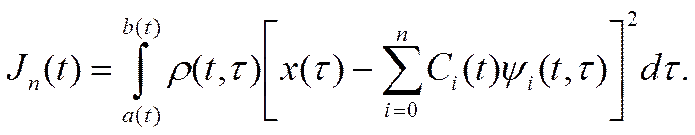
Нетрудно показать, что минимум функции J_n(t) в каждый момент t достигается, если коэффициенты С_i(t) являются коэф­фициентами Фурье, определяемыми формулами

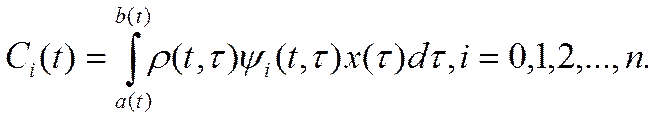
Минимальное значение меры точности определяется выражением

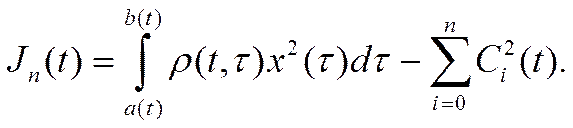
Систему нестационарных ортогональных функций будем назы­вать замкнутой, если справедливо соотношение

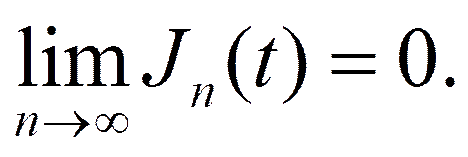
Любая система нестационарных ортогональных многочленов, а также системы нестационарных тригонометрических функций, рассмотренных выше, на конечном отрезке являются замкнутыми, что следует из замкнутости соответствующих стационарных систем.

Ряд Фурье является нестационарным, поскольку на нестационарном отрезке меняются как базисные функции

ψ_i(t,τ), так и коэффициенты Фурье С_i(t). Последние есть функ­ции переменной t, от которой зависят концы отрезка.

Функция X(i, t), ординатами которой являются коэффици­енты Фурье функции х(τ), представляет собой одномерную спект­ральную характеристику функции х(τ) по нестационарному ортонормированному базису {ψ_i(t, τ)}, называемую в дальнейшем просто нестационарной спектральной характери­стикой. Нестационарная спектральная характеристика X(i, t), согласно выражению , определяется формулой

(*)

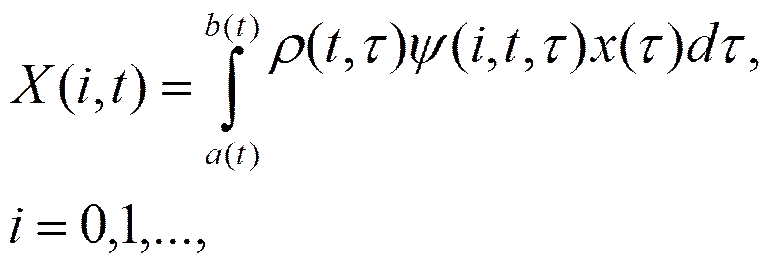где ψ(i, t, τ) = ψ_i(t, τ)} - общий член ортонормированной системы {ψ_i(t, τ)}.

Нестационарная спектральная характеристика является функ­цией двух аргументов: дискретного аргумента i и непрерыв­ного t. Она описывает свойства функции времени на переменном отрезке времени [a(t), b(t)], а при фиксированном аргументе t = ts - на стационарном отрезке времени [a(t_s), b (t_s)].

Нестационарная спектральная характеристика может быть пред­ставлена в виде матрицы — столбца с бесконечным числом эле­ментов, которыми являются ординаты спектральной характери­стики С_i(t):

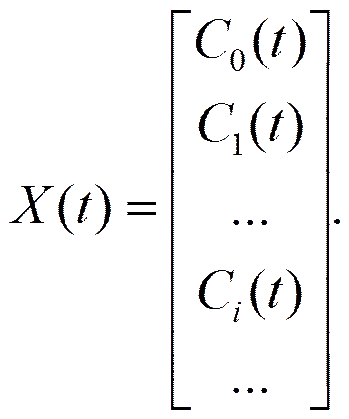
Если требуется представить нестационарную спектральную характеристику матрицей-строкой, то будем последнюю опреде­лять как транспонированную матрицу X^T(t) .

Обратный переход от спектральной характеристики к функ­ции времени осуществляется по формуле

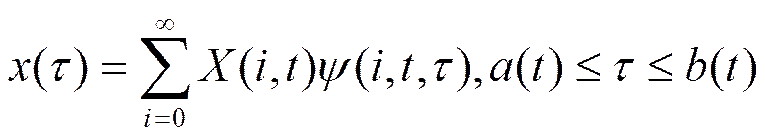
и практически может быть произведен путем численного или графического суммирования конечного числа членов ряда . Поскольку нестационарный ряд Фурье является функцией боль­шего числа независимых переменных, чем аппроксимируемая функ­ция, то обратный переход можно выполнить двумя способами. Так, можно суммировать конечное число членов сечения ряда при фиксированном аргументе t = t_s:

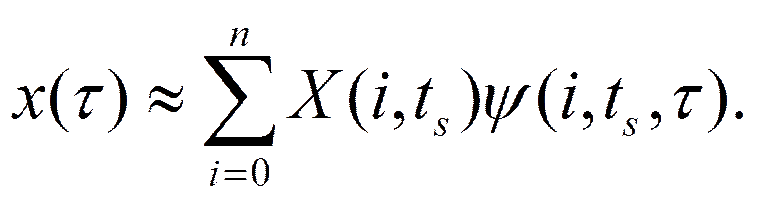
Очевидно, что в этом случае восстанавливаемая функция будет найдена как функция времени τ в пределах стационарного отрезка a(t_s)≤τ≤b(t_s). Кроме того, восстанавливаемая функция может быть найдена как функция времени t путем суммирования конечного числа членов сечения ряда при τ = t:

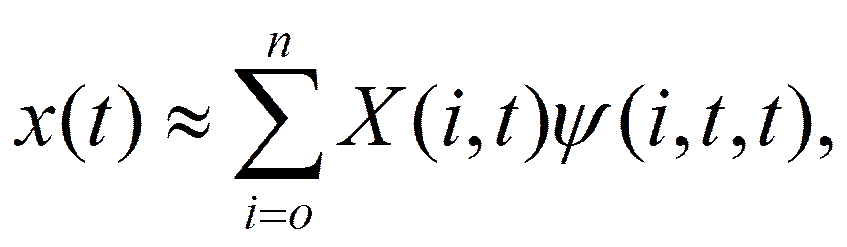
если ψ(i, t, t) определено и тождественно не равно нулю, как, например, функции системы .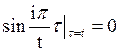

Указан­ная особенность обратного перехода к функции времени имеет место и для двумерных нестационарных разложений.

Нестационарные спектральные характеристики дельта - функ­ции и ее производных вычисляются по общей формуле (*).