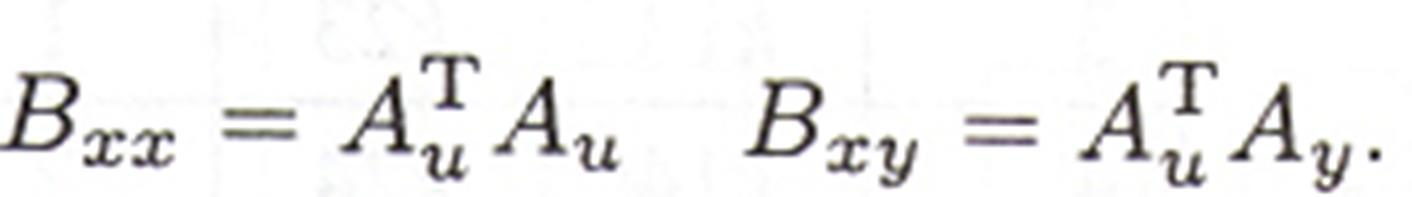Восстановление на основе адаптивного линейного преобразователя

Наиболее удобной для практического использования является структура преобразователя, представляющая собой сумматор, в контур отрицательной обратной связи которого включен оператор c импульсной переходной функцией _Kр*_K(t).

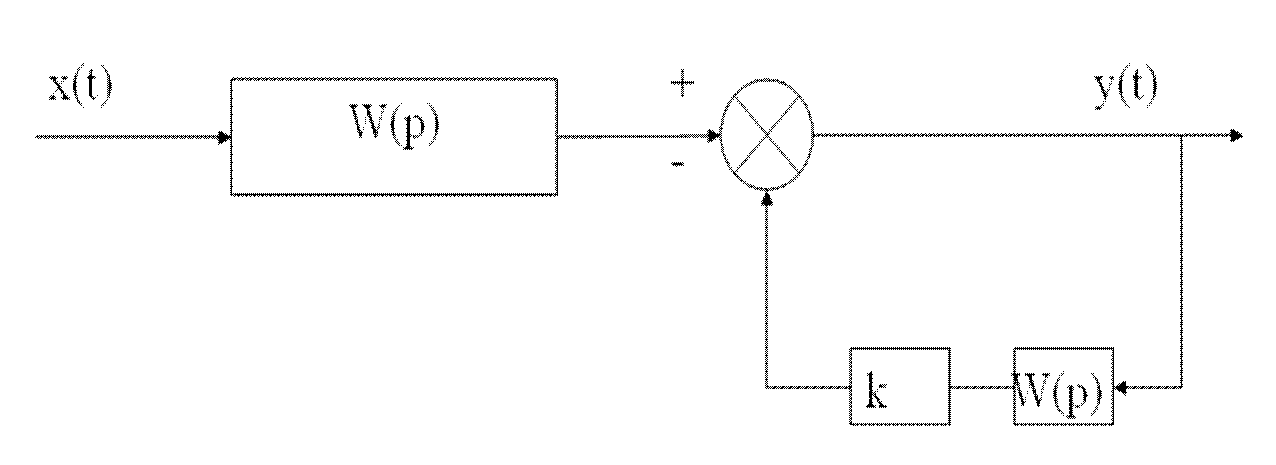
Рис. Структура адаптивного линейного преобразователя для оперативного восстановления входного сигнала

Передаточная функция оператора имеет

Wпр=(1+ _Kр*_W)^-1. Для исключения ошибки датчика в установившемся состоянии при единичном входном сигнале оператор W необходимо умножить на (_Kр*_K+1). Здесь _K – коэффициент усиления датчика. При этом время измерения постоянной величины сокращается и не имеет систематической ошибки. Динамические свойства системы датчик - восстанавливающий оператор (ДВО) существенно улучшаются. Так для датчика, описываемого колебательным звеном второго порядка и с постоянной времени Т, получаем оператор ДВО в виде звена второго порядка с меньшей постоянной времени.

Однако, увеличение _Kр приводит при наличии помех к снижению помехоустойчивости данного подхода. Это связано с тем, что фактически используется псевдообратный оператор.

Этот метод основан на представлении объекта системой дифференциальных уравнений.

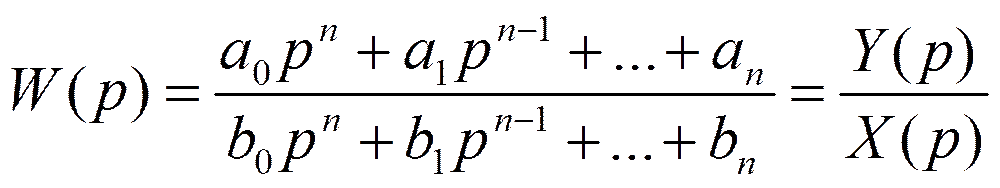
Сократим уравнение на 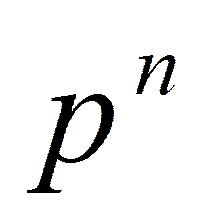и получим:

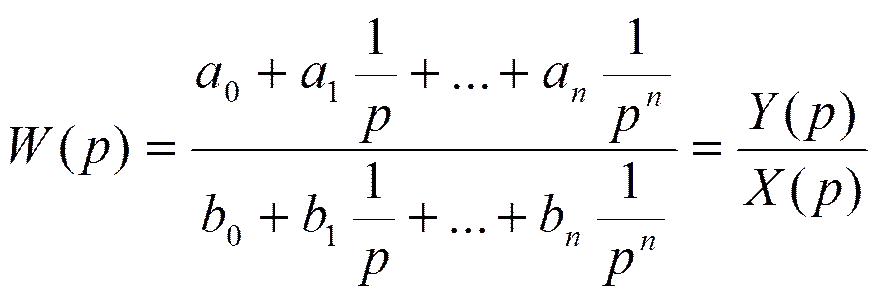
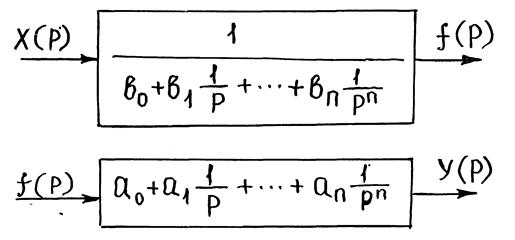
Рисунок – Модель системы

Отношение f(p) к X(p):

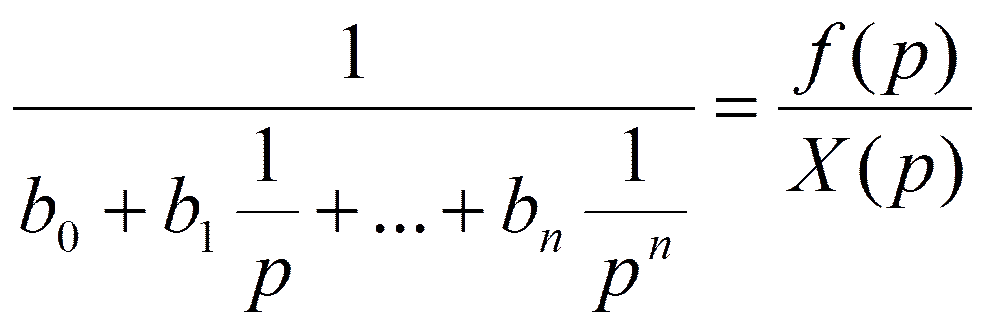
Отсюда находим X(p):

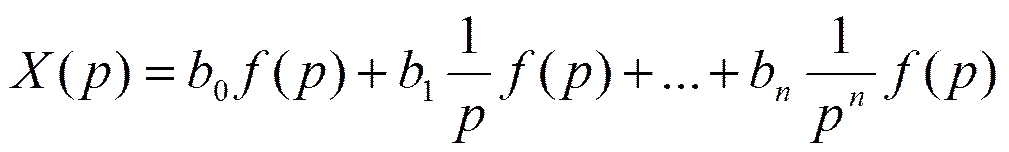
Возьмем 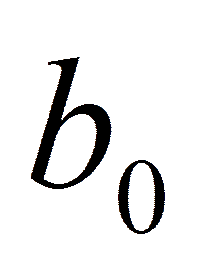=1.

Получаем:

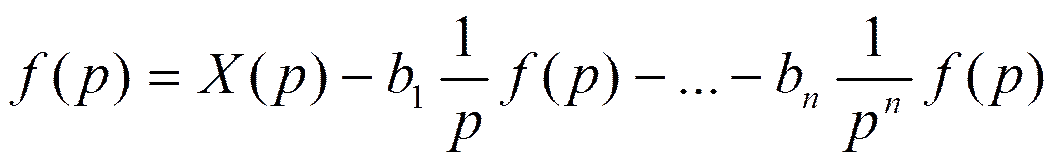
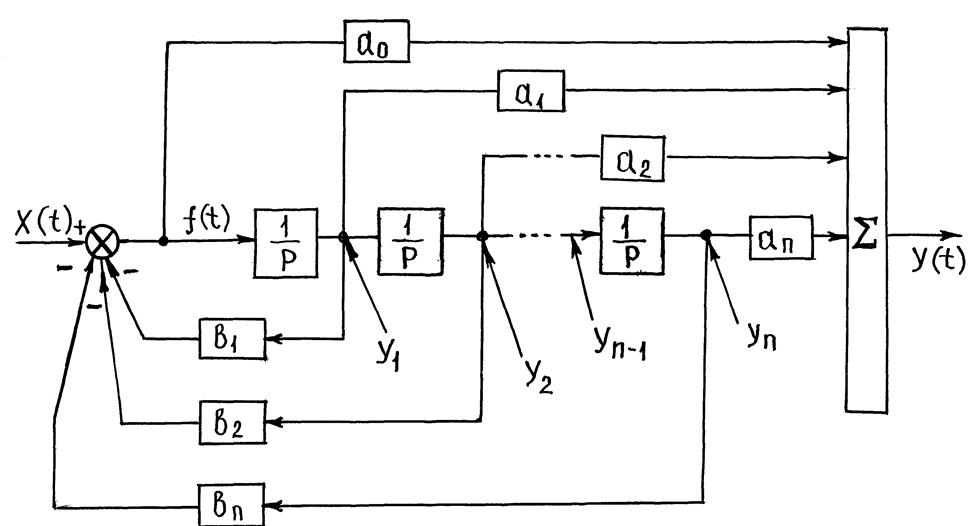
Исходная схема представлена на рисунке.

Рисунок – схема реализации динамической системы

Получаем систему, которая в дальнейшем реализовывается в пакете Mathcad.

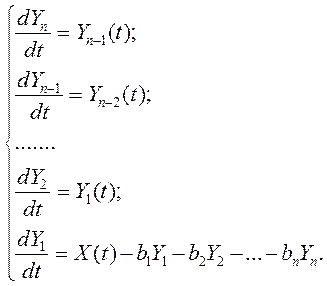
Выходной сигнал:

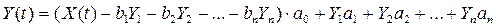
Рассмотрим пример, вычисления которого проводились в Mathcad.

Сигнал имеет вид:

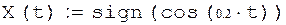Начальные условия равны нулю:

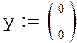Составляем систему уравнений:

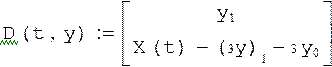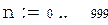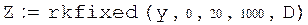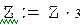Получаем восстановленный входной сигнал (синий) и выходной сигнал датчика (красный).

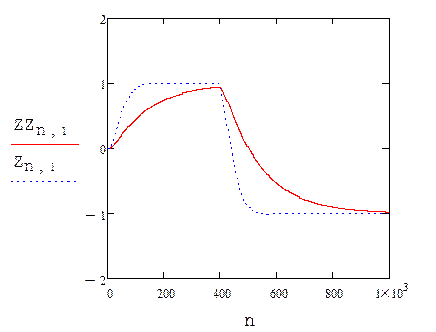Рисунок – Результат восстановления входного сигнала.

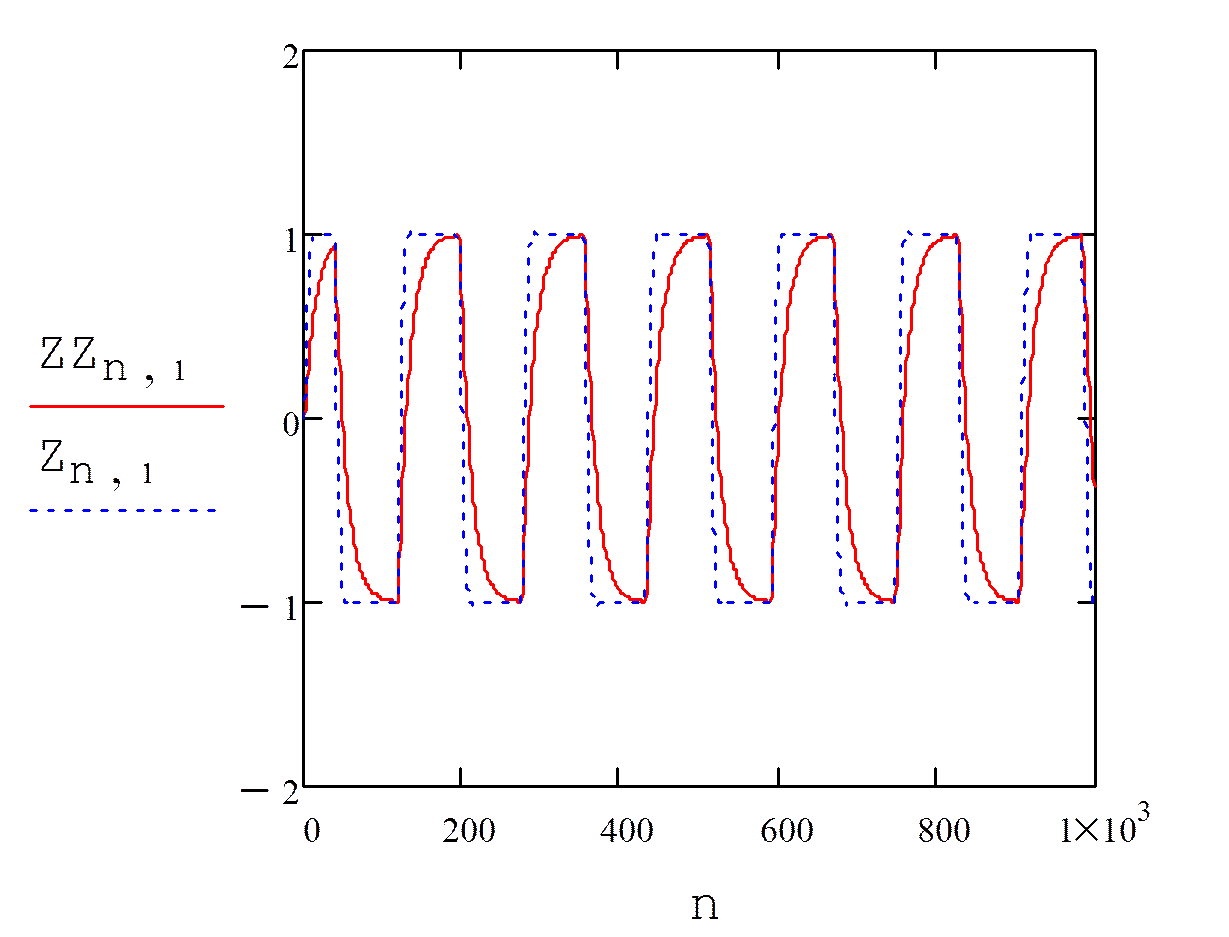
Рисунок – Восстановление входного сигнала на большом интервале (синий) по результатам наблюдения выходного сигнала (красный)

Зададим процесс с ненулевыми начальными условиями:

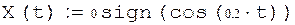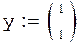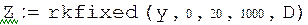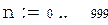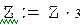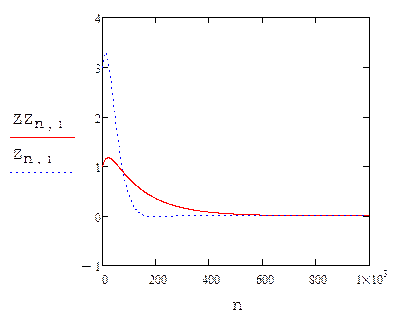Рисунок – Влияние начальных условий на выходной сигнал

На рисунке видно, что при использовании системы восстановления входного сигнала влияние начальных условий сокращается по времени.

Пример 3.Параметрическая идентификация (адаптивная)

Пусть динамический объект имеет вид:

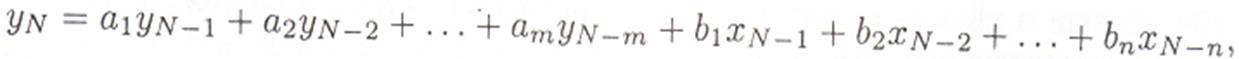
где - выход объекта, х - вход, т - глубина памяти по выходу, п - глубина памяти по входу.

Введем расширенный вектор входов

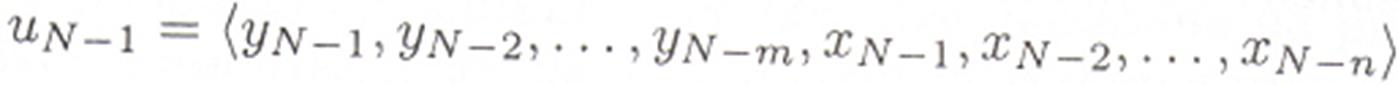
и параметров

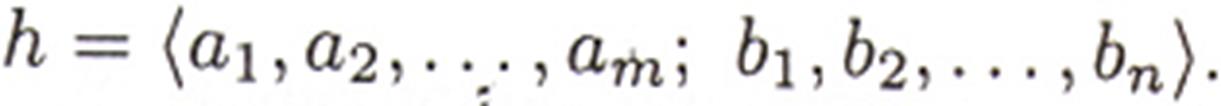
Вектора имеют размерность

С учетом вектора уравнение объекта может быть записано в виде

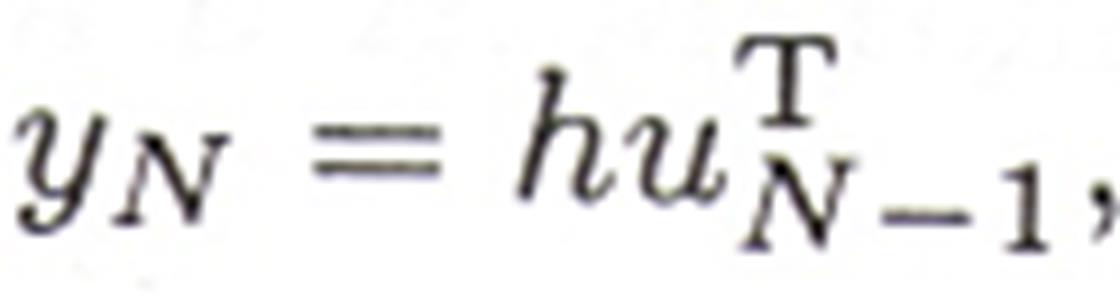
где Т - знак транспонирования.

Будем предполагать, что модель имеет ту же структуру, то есть

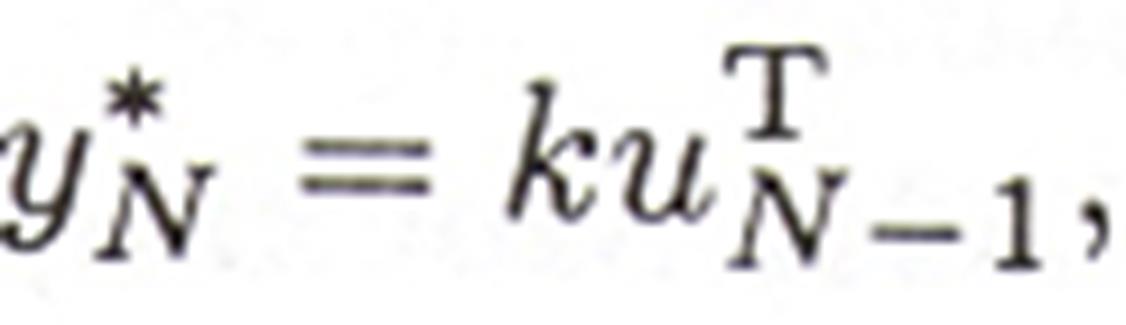
где k - вектор оценок параметров объекта h.

Дополнительно задана некоторая априорная информация об области изменения параметров объекта h, заданная, например, в виде условий устойчивости.

Наша цель создать алгоритм получения оценок параметров объектапо экспериментальным данным с учетом априорной информации.(Адаптация по m,n ).

Преобразование исходных данных

Матрица исходных данных 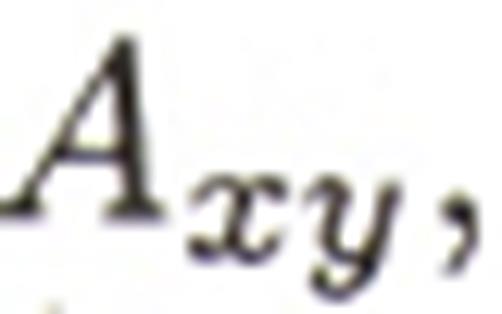полученных непосредственно с объекта, для одного входа имеет два столбца (1 вход + 1 выход) и (N + s) строк по числу проведенных экспериментов

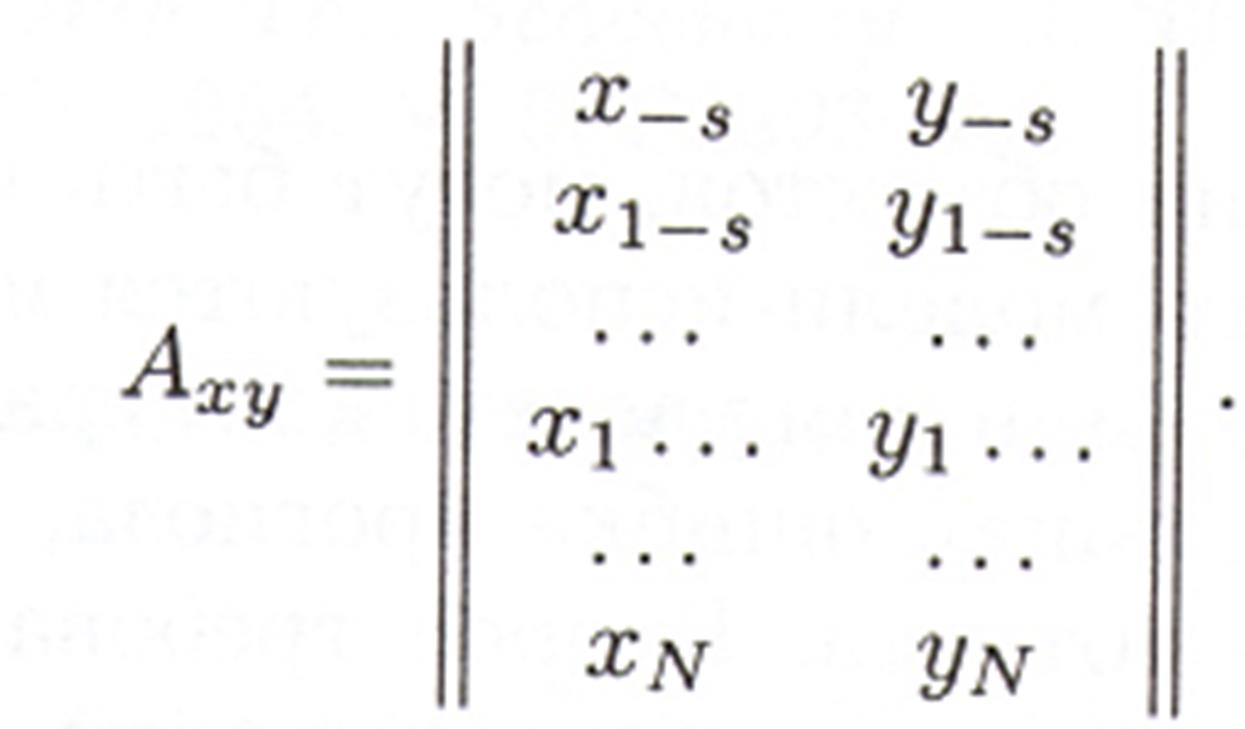
Если объект имеет l входов, то матрица исходных данных будет иметь ( l + 1)

столбец. Ниже будем рассматривать динамические объекты только с одним входом, поскольку обобщение на многие входы очевидно.

Для дальнейшей обработки в соответствии с расширенным входным вектором (2.2) матрицу исходных данных 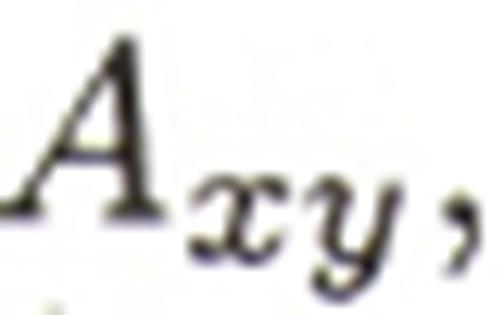необходимо разбить на две матрицы: матрицу данных о входах А_u размером (s х N ) и матрицу данных о выходах Ау размером (1 х N ).

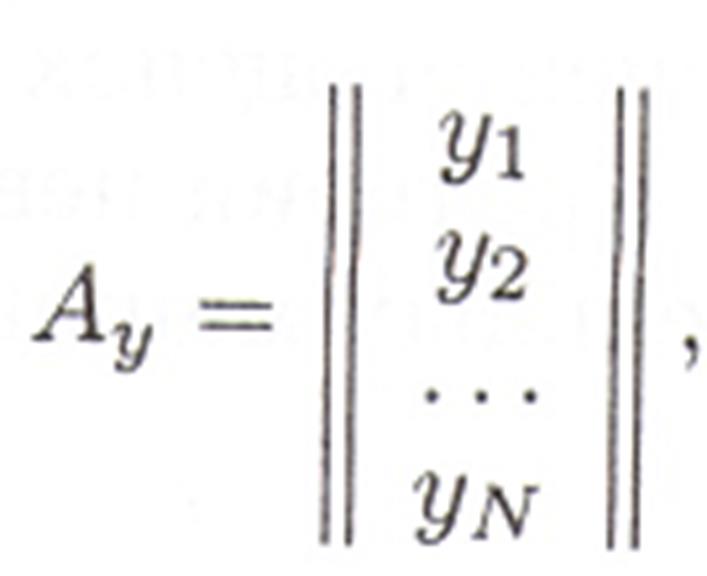
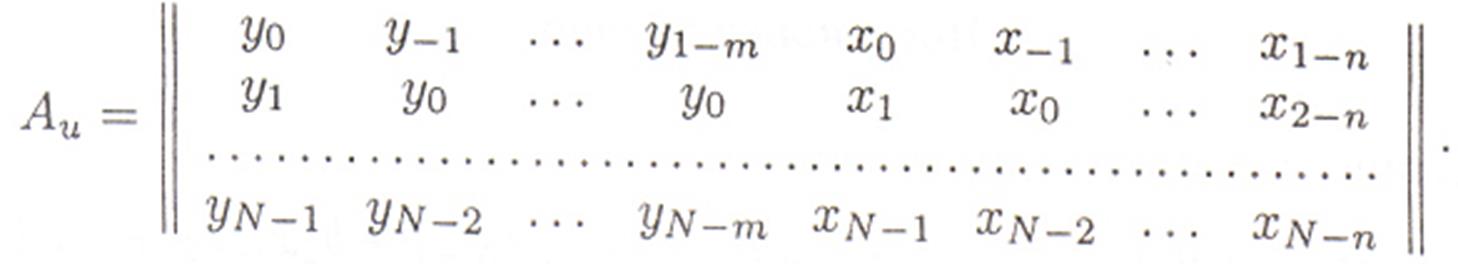
Отметим, что для получения оценок k неизвестных параметров h, по методу наименьших квадратов, используя исходные данные , необходимо решить систему уравнений

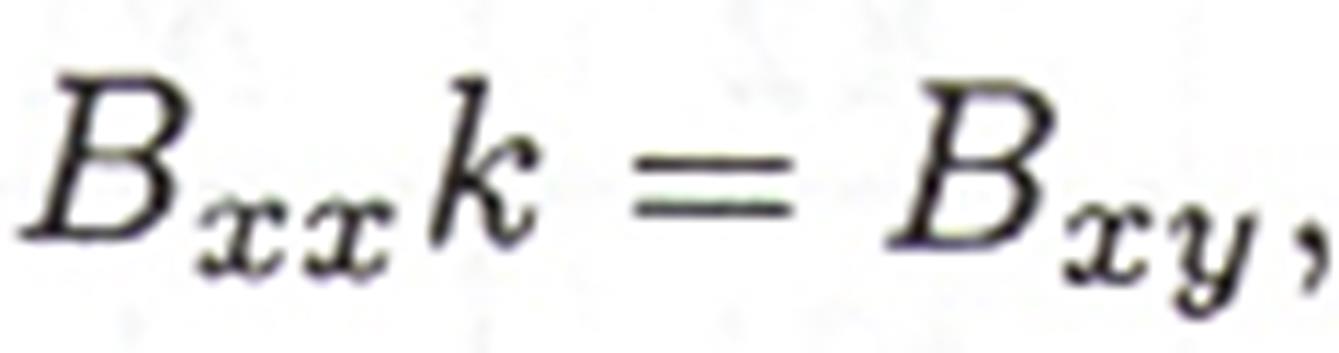
где матрицы Вхх (размер (s х s)) и Вху (размер (1 х s)) вычисляются через преобразованную матрицу входов А_u и матрицу выходов Ау по формулам:

(2.10)