Оптимальное восстановление входного сигнала

В данном разделе рассматриваются помехоустойчивое восстановление и преобразование сигнала, искаженного линейной инерционной системой. Примером такой системы может служить любой инерционный датчик. А поскольку именно датчики являются основным источником информации для работы автоматических и автоматизированных систем, проблема оперативного восстановления и преобразования сигнала встает особенно остро.

Одним из возможных способов повышения устойчивости и точности оценок входного сигнала является сужение класса функций восстанавливаемого входного сигнала.

В данном пособии принята на интервале наблюдения модель входного сигнала полиномиального типа

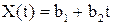. (47)

В качестве моделей линейной динамической измерительной системы приняты передаточные функции вида [16]:

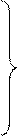
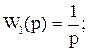
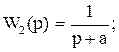
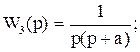
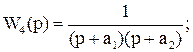(48)

,

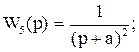
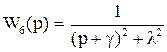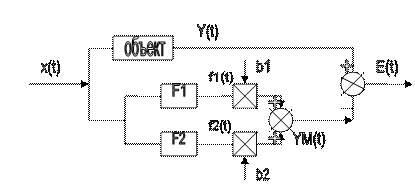
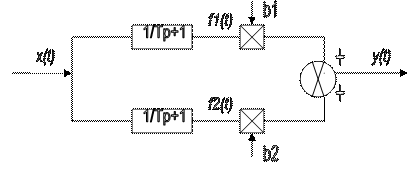
с помощью которых могут быть описаны различные классы измерительных систем. Расчетная схема формирования наблюдаемого сигнала системы оптимальной коррекции динамических погрешностей измерений системой W(p) представлена на рис. 2.

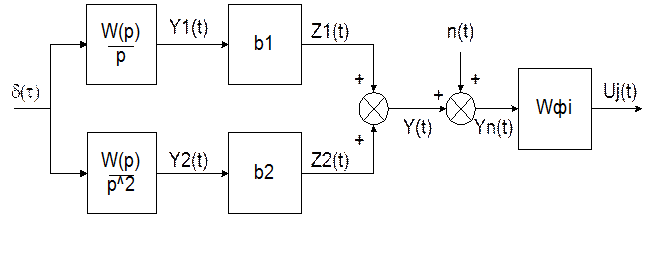Рис. 2. Схема оптимальной фильтрации при наличии помехи типа «белый шум»

Необходимо синтезировать линейные фильтры Wfi, i=1,2, выделяющие с наименьшей дисперсией ошибки из выходного сигнала измерительной системы Y_H(t) составляющие, пропорциональные контролируемым параметрам b₁,b₂,…,b_n. Сигналы Z₁(t), Z₂(t) (рис. 2) являются случайными из-за случайности параметров b₁,b₂. Желаемым выходным сигналом m_j(t) синтезируемого линейного фильтра W_fj является сигнал

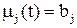_. (49)

Сформируем ошибку при определении параметра b_j с помощью фильтра W_fj в виде

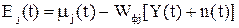(50)

и определим оператор W_fj из условия минимума дисперсии этой ошибки

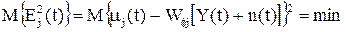. (51)

Рассмотрим вначале решение данной задачи для случая помехи n(t) типа белого шума с корреляционной функцией R_n(t) = n*d(|t|). Затем на основе данного решения произведем обобщение на случай произвольной помехи.

Оптимальные несмещенные оценки 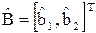в случае помехи типа белого шума определяются соотношениями:

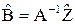. (52)

Элементы матрицы А и вектора 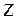равны

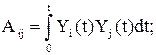(53)

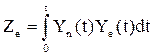. (54)

Точность оценок характеризуется дисперсионной матрицей ошибок

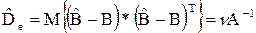, (55)

где n – интенсивность белого шума.

В случае дискретных измерений выходного сигнала измерительной системы в моменты t=nT уравнения (53), (54) перепишутся в виде

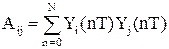, (56)

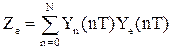. (57)

Синтезируем на основе рассмотренной схемы рис. 2 оптимальный фильтр в случае помехи, отличной от белого шума.

Преобразуем расчетную схему, представленную на рис.2. Помеха n(t) характеризуется нулевым математическим ожиданием и корреляционной функцией R_n(t). Будем искать оптимальный фильтр в виде последовательного соединения двух звеньев F₁ и F_2j, j=1,2. Звено F₁ такое, что преобразует стационарную произвольную помеху n(t) в стационарный белый шум. Эквивалентная расчетная схема представлена на рис. 3.

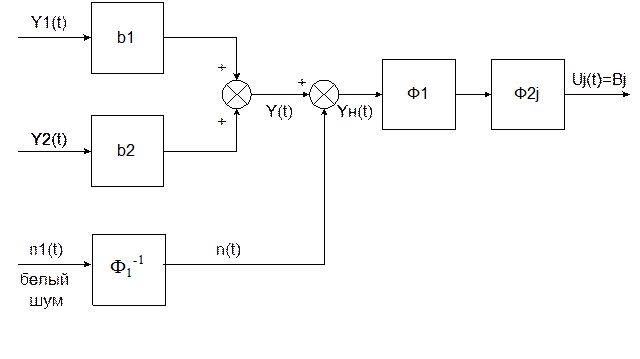
Рис. 3. Схема оптимальной фильтрации при помехе, отличной от белого шума

Здесь F₁^-1 представляет собой формирующий фильтр для помехи n(t) c корреляционной функцией R_n(t). Окончательно схему (рис.3) можно представить в виде рис. 4.

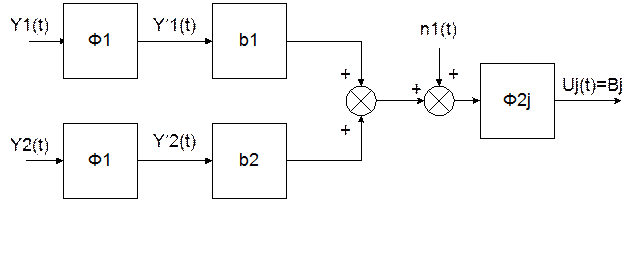
Рис. 4. Преобразованная схема оптимальной фильтрации при помехе,

отличной от белого шума

Таким образом, предлагаемая выше методика синтеза оптимальных фильтров на основе соотношений (52)-(57) может быть применена и для случая синтеза фильтров при произвольной помехе.

Получение математической модели динамического промышленного объекта.

,

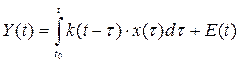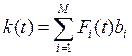- импульсная переходная функция,

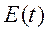-помеха типа белого шума.

Подставляем 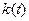в .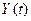

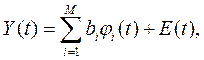
где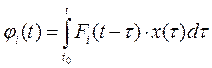

Если 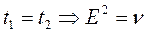, то уравнение 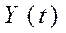перепишем в матричной форме : .

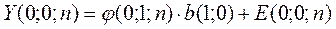Это выражение полностью соответствует выражению для прогнозирования, поэтому оценка b :

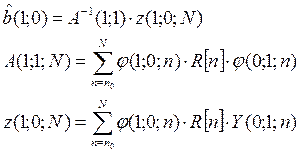
Точность определенного параметра b оценивается дисперсиями этих параметров, т.е. диагональными элементами матрицы D.

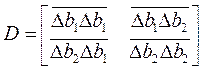
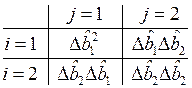
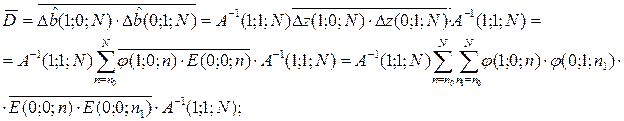
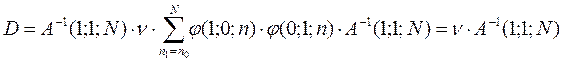
Критерии оптимизации.

1. Минимизация следа матрицы -это сумма диагональных элементов матрицы .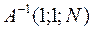

2. Максимизация определителя .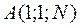

3. Независимое определение параметра .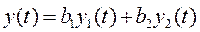

Рассмотрим на примере.

Для определения 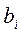входной сигнал 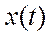выбирается так, чтобы

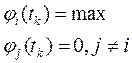
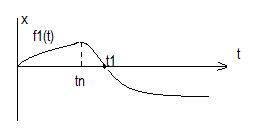
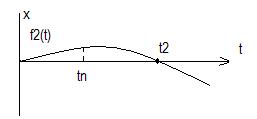
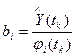
Поиск оптимального значения соответствующего критерия осуществляется на основе минимизации функции многих переменных.

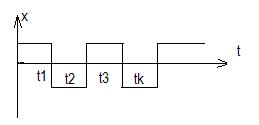
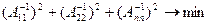, подбирая 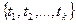при наличии линейных ограничений :

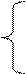
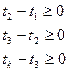
Качественное описание необходимости планирования эксперимент

Связь между входным и выходным сигналом :

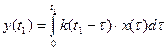
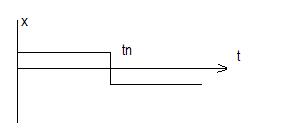
Подаем на вход единичный скачок x(t)=1(t) на выходе получим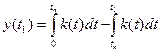

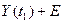- коэффициент влияния помехи будет большим.

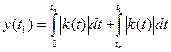
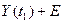-малое влияние помехи.

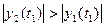
Замкнутый метод идентификации динамического объекта на основе градиентного метода.